I am attempting to graph data (here, a sine wave) in polar coordinates in ggplot, but am seeing undesired behavior and am questioning my approach.
Below is my reprex/ thought process.
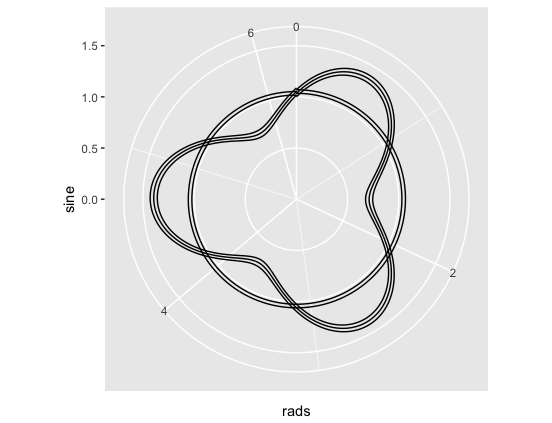
The problem I want to solve: unwanted gaps as shown in attempt 4.
More generally, is my plotting approach correct?
Thank you
library(tidyverse)
# first, generate some data: 2*pi radians in a circle; we have three circles' worth of rads
x <- tibble(x = head(seq(0, 3 * (2 * pi), by = pi / 180), -1))
# compute our sine wave; also, we may need to compute rads, because we'll want our plot theta
# to be restricted from 0 to 2pi, and as far as the axis is concerned, 2pi = 4pi = 6pi = etc
x <- x %>% mutate(sine = sin(3*x)/3 + 1 + x/180, rads = x %% (2*pi))
# Attempt 1
ggplot(x) +
geom_line(aes(x = x, y = sine)) +
ylim(c(0,1.5)) +
coord_polar(theta = 'x')
## THE PROBLEM: the above spreads the theta over the entire x,
# ie, it ranges up to 3 * (2 * pi), instead of the standard 2*pi
# Attempt 2. Let's change the x aes to our rads variable
ggplot(x) +
geom_line(aes(x = rads, y = sine)) +
ylim(c(0,1.5)) +
coord_polar(theta = 'x')
## THE PROBLEM: this generates strange behavior, with plotting jumping around, but at least theta is on 0,2*pi
# Attempt 3. since the values of the sine are in order, maybe I can use geom_path...
ggplot(x) +
geom_path(aes(x = rads, y = sine)) +
ylim(c(0,1.5)) +
coord_polar(theta = 'x')
## THE PROBLEM: this looks a little better, but the plot is drawing circles at each 0/2*pi transition
# Attempt 4: let's try adding a grouping variable
y <- x %>% mutate(circle_no = rep(1:3, each = 2*180))
ggplot(y) +
geom_path(aes(x = rads, y = sine, group = circle_no)) +
ylim(c(0,1.5)) +
coord_polar(theta = 'x')
Incidentally, if I inspect a simple linear graph of the sine wave, I don't see any discontinuities...
ggplot(y) + geom_path(aes(x = x, y = sine))