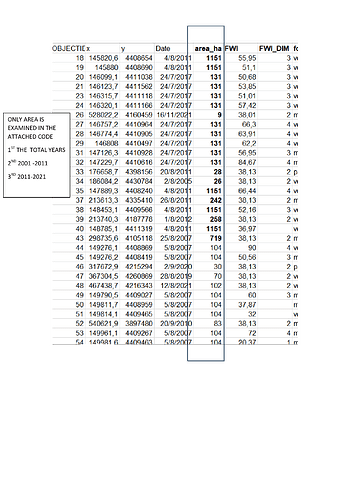
This is great. Don't need all the data, just enough to work the problem. The output is just an odd way of showing a data frame. Assigning it to d comes out looking like this
> head(d)
Date area_ha
1 2021-05-19 7005
2 2021-05-19 7005
3 2021-05-19 7005
4 2021-05-19 7005
5 2021-05-19 7005
6 2021-05-19 7005
Starting now on the main event. ... [later]
Had some difficulty interpreting their methodology.
library(ggplot2)
#> Warning: package 'ggplot2' was built under R version 4.3.1
RandomF <- structure(list(
Date = structure(c(
1621382400, 1621382400, 1621382400,
1621382400, 1621382400, 1621382400, 1621382400, 1621382400, 1621382400,
1621382400, 1621382400, 1621382400, 1156204800, 1156204800, 1156204800,
1156204800, 1156204800, 1156204800, 1156204800, 1156204800, 1156204800,
1156204800, 1156204800, 1156204800, 1314144000, 1314144000, 1314144000,
1314144000, 1314144000, 1314144000, 1314144000, 1314144000, 1314144000,
1314144000, 1314144000, 1314144000, 1314144000, 1314144000, 1314144000,
1314144000, 1314144000, 1314144000, 1314144000, 1314144000, 1314144000,
1314144000, 1314144000, 1314144000, 1183075200, 1183075200, 1183075200,
1183075200, 1183075200, 1183075200, 1183075200, 1183075200, 1183075200,
1183075200, 1183075200, 1183075200, 1183075200, 1183075200, 1250899200,
1250899200, 1250899200, 1250899200, 1250899200, 1250899200, 1250899200,
1250899200, 1250899200, 1250899200, 1250899200, 1250899200, 1250899200,
1250899200, 1250899200, 1250899200, 1250899200, 1250899200, 1250899200,
1250899200, 1250899200, 1532304000, 1532304000, 1532304000, 1532304000,
1532304000, 1532304000, 1532304000, 1532304000, 1532304000, 1532304000,
1532304000, 1532304000, 1532304000, 1532304000, 1187913600, 1187913600,
1187913600, 1187913600, 1187913600, 1187913600, 1187913600, 1187913600,
1187913600, 1187913600, 1187913600, 1187913600, 1187913600, 1187913600,
1187913600, 1187913600, 1187913600, 1187913600, 1187913600, 1187913600,
1187913600, 1187913600, 1187913600, 1187913600, 1469404800, 1377648000,
1377648000, 1377648000, 1377648000, 1377648000, 1377648000, 1377648000,
1377648000, 1377648000, 1377648000, 1377648000, 1377648000, 1377648000,
1344384000, 1344384000, 1344384000, 1344384000, 1344384000, 1344384000,
1344384000, 1344384000, 1344384000, 1344384000, 1344384000, 1344384000,
1156118400, 1156118400, 1156118400, 1156118400, 1156118400, 1156118400,
1156118400, 1156118400, 1156118400, 1156118400, 1156118400, 1156118400,
1156118400, 1156118400, 1156118400, 1156118400, 1156118400, 1156118400,
1156118400, 1156118400, 1156118400, 1156118400, 1156118400, 1156118400,
1156118400, 1156118400, 1156118400, 1156118400, 1156118400, 1156118400,
1156118400, 1156118400, 1156118400, 1156118400, 1156118400, 1156118400,
1156118400, 1156118400, 1156118400, 1156118400, 1156118400, 1156118400,
1156118400, 1156118400, 1156118400, 1156118400, 1156118400, 1156118400,
1156118400, 1156118400, 1156118400, 1156118400, 1156118400, 1156118400,
1156118400, 1156118400, 1156118400, 1156118400, 1156118400, 1156118400,
1156118400, 1156118400, 1156118400, 1156118400, 1156118400, 1156118400,
1156118400, 1156118400, 1156118400, 1156118400, 1156118400, 1156118400,
1156118400, 1156118400, 1156118400, 1156118400, 1156118400, 1156118400,
1156118400, 1156118400, 1156118400, 1156118400, 1156118400, 1156118400,
1628121600, 1628121600, 1628121600, 1628121600, 1182988800, 1182988800,
1182988800, 1182988800, 1182988800, 1182988800, 1182988800, 1182988800,
1182988800, 1182988800, 1182988800, 1182988800, 1182988800, 1182988800,
1182988800, 1374883200, 1374883200, 1374883200, 1374883200, 1374883200,
1374883200, 1374883200, 1374883200, 1374883200, 1374883200, 1374883200,
1374883200, 1374883200, 1374883200, 1437091200, 1437091200, 1437091200,
1437091200, 1437091200, 1437091200, 1437091200, 1437091200, 1437091200,
1437091200, 1437091200, 1437091200, 1473465600, 1473465600, 1473465600,
1473465600, 1473465600, 1473465600, 1473465600, 1473465600, 1473465600,
1473465600, 1473465600, 1473465600, 1473465600, 1473465600, 1473465600,
1473465600, 1473465600, 1473465600, 1473465600, 1473465600, 1473465600,
1473465600, 1473465600, 1473465600, 1473465600, 1473465600, 1345852800,
1345852800, 1345852800, 1345852800, 1345852800, 1345852800, 1345852800,
1345852800, 1345852800, 1345852800, 1345852800, 1345852800, 1345852800,
1345852800, 1345852800, 1345852800, 1345852800, 1345852800, 1345852800,
1345852800, 1345852800, 1345852800, 1345852800, 1595376000, 1595376000,
1595376000, 1595376000, 1595376000, 1595376000, 1595376000, 1595376000,
1595376000, 1595376000, 1339804800, 1339804800, 1339804800, 1339804800,
1339804800, 1339804800, 1339804800, 1339804800, 1339804800, 1339804800,
1339804800, 1339804800, 1250899200, 1250899200, 1250899200, 1250899200,
1250899200, 1250899200, 1250899200, 1250899200, 1250899200, 1250899200,
1250899200, 1250899200, 1250899200, 1501804800, 1501804800, 1501804800,
1501804800, 1501804800, 1501804800, 1501804800, 1501804800, 1501804800,
1501804800, 1501804800, 1628121600, 1628121600, 1628121600, 1628121600,
1628121600, 1628121600, 1628121600, 1628121600, 1628121600, 1628121600,
1628121600, 1628121600, 1565568000, 1565568000, 1565568000, 1565568000,
1565568000, 1565568000, 1565568000, 1565568000, 1565568000, 1565568000,
1565568000, 1311897600, 1311897600, 1311897600, 1311897600, 1311897600,
1311897600, 1311897600, 1311897600, 1311897600, 1311897600, 1311897600,
1311897600, 1311897600, 1311897600, 1311897600, 1185408000, 1185408000,
1185408000, 1185408000, 1185408000, 1185408000, 1185408000, 1185408000,
1185408000, 1185408000, 1185408000, 1185408000, 1185408000, 1502582400,
1502582400, 1502582400, 1502582400, 1502582400, 1502582400, 1502582400,
1502582400, 1502582400, 1502582400, 1502582400, 1502582400, 1502582400,
1.188e+09, 1.188e+09, 1.188e+09, 1.188e+09, 1.188e+09, 1.188e+09,
1.188e+09, 1.188e+09, 1.188e+09, 1.188e+09, 1.188e+09, 1.188e+09,
1.188e+09, 1.188e+09, 1.188e+09, 1.188e+09, 1.188e+09, 1.188e+09,
1.188e+09, 1.188e+09, 1.188e+09, 1.188e+09, 1469836800, 1469836800,
1469836800, 1469836800, 1469836800, 1469836800, 1469836800, 1469836800,
1469836800, 1469836800, 1469836800, 1469836800, 1403740800, 1403740800,
1403740800, 1403740800, 1403740800, 1403740800, 1403740800, 1403740800,
1403740800, 1403740800, 1403740800, 1403740800, 1185321600, 1185321600,
1185321600, 1185321600, 1185321600, 1185321600, 1185321600, 1185321600,
1185321600, 1185321600, 1185321600, 1185321600, 1185321600, 1185321600,
1185321600, 1185321600, 1185321600, 1185321600, 1185321600, 1185321600,
1185321600, 1185321600, 1185321600, 1185321600, 1185321600, 1185321600,
1185321600, 1185321600, 1185321600, 1185321600, 1185321600, 1185321600,
1185321600, 1185321600, 1185321600, 1185321600, 1185321600, 1185321600,
1185321600, 1185321600, 1185321600, 1185321600, 1185321600, 1185321600,
1185321600, 1185321600, 1185321600, 1185321600, 1185321600, 1185321600,
1185321600, 1185321600, 1185321600, 1185321600, 1185321600, 1185321600,
1185321600, 1185321600, 1185321600, 1185321600, 1185321600, 1185321600,
1185321600, 1185321600, 1185321600, 1185321600, 1185321600, 1185321600,
1185321600, 1185321600, 1185321600, 1185321600, 1185321600, 1185321600,
1185321600, 1185321600, 1185321600, 1185321600, 1185321600, 1185321600,
1185321600, 1185321600, 1185321600, 1185321600, 1218672000, 1218672000,
1218672000, 1218672000, 1218672000, 1218672000, 1218672000, 1218672000,
1218672000, 1218672000, 1218672000, 1314230400, 1314230400, 1314230400,
1314230400, 1314230400, 1314230400, 1314230400, 1314230400, 1314230400,
1314230400, 1314230400, 1498867200, 1498867200, 1498867200, 1498867200,
1498867200, 1498867200, 1498867200, 1498867200, 1498867200, 1498867200,
1.188e+09, 1.188e+09, 1.188e+09, 1.188e+09, 1.188e+09, 1.188e+09,
1.188e+09, 1.188e+09, 1.188e+09, 1.188e+09, 1.188e+09, 1.188e+09,
1314057600, 1314057600, 1314057600, 1314057600, 1314057600, 1314057600,
1314057600, 1314057600, 1314057600, 1314057600, 1314057600, 1314057600,
1314057600, 1185062400, 1185062400, 1185062400, 1185062400, 1185062400,
1185062400, 1185062400, 1185062400, 1185062400, 1185062400, 1185062400,
1250467200, 1250467200, 1250467200, 1250467200, 1250467200, 1250467200,
1250467200, 1250467200, 1250467200, 1250467200, 1250467200, 1250467200,
1250467200, 1250467200, 1250467200, 1185321600, 1185321600, 1185321600,
1185321600, 1185321600, 1185321600, 1185321600, 1185321600, 1185321600,
1185321600, 1185321600, 1185321600, 1185321600, 1185321600, 1185321600,
1185321600, 1185321600, 1185321600, 1185321600, 1185321600, 1185321600,
1185321600, 1185321600, 1185321600, 1185321600, 1185321600, 1185321600,
1185321600, 1185321600, 1598054400, 1598054400, 1374883200, 1374883200,
1374883200, 1374883200, 1374883200, 1374883200, 1374883200, 1374883200,
1374883200, 1374883200, 1374883200, 1314316800, 1314316800, 1314316800,
1314316800, 1314316800, 1314316800, 1314316800, 1314316800, 1314316800,
1314316800, 1314316800, 1314316800, 1.188e+09, 1.188e+09, 1.188e+09,
1.188e+09, 1.188e+09, 1.188e+09, 1.188e+09, 1.188e+09, 1.188e+09,
1.188e+09, 1.188e+09, 1.188e+09, 1.188e+09, 1.188e+09, 1.188e+09,
1.188e+09, 1466208000, 1466208000, 1466208000, 1466208000, 1466208000,
1466208000, 1466208000, 1466208000, 1466208000, 1466208000, 1185321600,
1185321600, 1185321600, 1185321600, 1185321600, 1185321600, 1185321600,
1185321600, 1185321600, 1185321600, 1185321600, 1314316800, 1314316800,
1314316800, 1314316800, 1314316800, 1314316800, 1314316800, 1314316800,
1.188e+09, 1.188e+09, 1.188e+09, 1.188e+09, 1.188e+09, 1.188e+09,
1.188e+09, 1.188e+09, 1.188e+09, 1.188e+09, 1.188e+09, 1.188e+09,
1.188e+09, 1.188e+09, 1.188e+09, 1.188e+09, 1.188e+09, 1.188e+09,
1.188e+09, 1.188e+09, 1.188e+09, 1.188e+09, 1.188e+09, 1.188e+09,
1.188e+09, 1.188e+09, 1.188e+09, 1.188e+09, 1.188e+09, 1.188e+09,
1.188e+09, 1.188e+09, 1.188e+09, 1.188e+09, 1.188e+09, 1009843200,
1009843200, 1009843200, 1009843200, 1009843200, 1009843200, 1009843200,
1009843200, 1009843200, 1009843200, 1009843200, 1009843200, 1009843200,
1184803200, 1184803200, 1184803200, 1184803200, 1184803200, 1184803200,
1184803200, 1184803200, 1184803200, 1184803200, 1184803200, 1184803200,
1184803200, 1184803200, 1184803200, 1184803200, 1184803200, 1503705600,
1503705600, 1503705600, 1503705600, 1503705600, 1503705600, 1503705600,
1503705600, 1469404800, 1469404800, 1469404800, 1469404800, 1469404800,
1469404800, 1469404800, 1469404800, 1469404800, 1469404800, 1469404800,
1185321600, 1185321600, 1185321600, 1185321600, 1185321600, 1185321600,
1185321600, 1185321600, 1185321600, 1185321600, 1185321600, 1185321600,
1185321600, 1187913600, 1187913600, 1187913600, 1187913600, 1187913600,
1187913600, 1187913600, 1187913600, 1187913600, 1187913600, 1187913600,
1250726400, 1250726400, 1250726400, 1250726400, 1250726400, 1250726400,
1250726400, 1250726400, 1250726400, 1250726400, 1250726400, 1505174400,
1505174400, 1505174400, 1505174400, 1505174400, 1505174400, 1505174400,
1505174400, 1505174400, 1505174400, 1505174400, 1314316800, 1314316800,
1314316800, 1314316800, 1314316800, 1314316800, 1314316800, 1314316800,
1469836800, 1469836800, 1314144000, 1314144000, 978307200, 978307200,
978307200, 978307200, 978307200, 978307200, 978307200, 978307200,
978307200, 978307200, 978307200, 1183075200, 1183075200, 1183075200,
1183075200, 1183075200, 1183075200, 1183075200, 1183075200, 1183075200,
1183075200, 1183075200, 1403827200, 1403827200, 1403827200, 1403827200,
1403827200, 1403827200, 1403827200, 1403827200, 1403827200, 1403827200,
1404432000, 1404432000, 1404432000, 1404432000, 1404432000, 1404432000,
1404432000, 1404432000, 1404432000, 1404432000, 1281830400, 1281830400,
1281830400, 1281830400, 1281830400, 1281830400, 1281830400, 1281830400,
1281830400, 1281830400, 1281830400, 1185408000, 1185408000, 1185408000,
1185408000, 1185408000, 1185408000, 1185408000, 1185408000, 1185408000,
1185408000, 1185408000, 1185408000, 1185408000, 1188259200, 1188259200,
1188259200, 1188259200, 1188259200, 1188259200, 1188259200, 1188259200,
1188259200, 1188259200, 1188259200, 1188259200, 1188259200, 1532304000,
1532304000, 1532304000, 1532304000, 1532304000, 1532304000, 1188172800,
1188172800, 1188172800, 1188172800, 1188172800, 1188172800, 1188172800,
1188172800, 1188172800, 1188172800, 1188172800, 1343606400, 1343606400,
1343606400, 1343606400, 1343606400, 1343606400, 1343606400, 1343606400,
1343606400, 1343606400, 1343606400, 1182988800, 1182988800, 1182988800,
1182988800
), tzone = "UTC", class = c("POSIXct", "POSIXt")),
area_ha = c(
7005, 7005, 7005, 7005, 7005, 7005, 7005, 7005,
7005, 7005, 7005, 7005, 6837, 6837, 6837, 6837, 6837, 6837,
6837, 6837, 6837, 6837, 6837, 6837, 6245, 6245, 6245, 6245,
6245, 6245, 6245, 6245, 6245, 6245, 6245, 6245, 6245, 6245,
6245, 6245, 6245, 6245, 6245, 6245, 6245, 6245, 6245, 6245,
5829, 5829, 5829, 5829, 5829, 5829, 5829, 5829, 5829, 5829,
5829, 5829, 5829, 5829, 5815, 5815, 5815, 5815, 5815, 5815,
5815, 5815, 5815, 5815, 5815, 5815, 5815, 5815, 5815, 5815,
5815, 5815, 5815, 5815, 5815, 5568, 5568, 5568, 5568, 5568,
5568, 5568, 5568, 5568, 5568, 5568, 5568, 5568, 5568, 5434,
5434, 5434, 5434, 5434, 5434, 5434, 5434, 5434, 5434, 5434,
5434, 5434, 5434, 5434, 5434, 5434, 5434, 5434, 5434, 5434,
5434, 5434, 5434, 5242, 4986, 4986, 4986, 4986, 4986, 4986,
4986, 4986, 4986, 4986, 4986, 4986, 4986, 4833, 4833, 4833,
4833, 4833, 4833, 4833, 4833, 4833, 4833, 4833, 4833, 4813,
4813, 4813, 4813, 4813, 4813, 4813, 4813, 4813, 4813, 4813,
4813, 4813, 4813, 4813, 4813, 4813, 4813, 4813, 4813, 4813,
4813, 4813, 4813, 4813, 4813, 4813, 4813, 4813, 4813, 4813,
4813, 4813, 4813, 4813, 4813, 4813, 4813, 4813, 4813, 4813,
4813, 4813, 4813, 4813, 4813, 4813, 4813, 4813, 4813, 4813,
4813, 4813, 4813, 4813, 4813, 4813, 4813, 4813, 4813, 4813,
4813, 4813, 4813, 4813, 4813, 4813, 4813, 4813, 4813, 4813,
4813, 4813, 4813, 4813, 4813, 4813, 4813, 4813, 4813, 4813,
4813, 4813, 4813, 4688, 4688, 4688, 4688, 4386, 4386, 4386,
4386, 4386, 4386, 4386, 4386, 4386, 4386, 4386, 4386, 4386,
4386, 4386, 4227, 4227, 4227, 4227, 4227, 4227, 4227, 4227,
4227, 4227, 4227, 4227, 4227, 4227, 4093, 4093, 4093, 4093,
4093, 4093, 4093, 4093, 4093, 4093, 4093, 4093, 4079, 4079,
4079, 4079, 4079, 4079, 4079, 4079, 4079, 4079, 4079, 4079,
3896, 3896, 3896, 3896, 3896, 3896, 3896, 3896, 3896, 3896,
3896, 3896, 3896, 3896, 3724, 3724, 3724, 3724, 3724, 3724,
3724, 3724, 3724, 3724, 3724, 3724, 3724, 3724, 3724, 3724,
3724, 3724, 3724, 3724, 3724, 3724, 3724, 3549, 3549, 3549,
3549, 3549, 3549, 3549, 3549, 3549, 3549, 3310, 3310, 3310,
3310, 3310, 3310, 3310, 3310, 3310, 3310, 3310, 3310, 3073,
3073, 3073, 3073, 3073, 3073, 3073, 3073, 3073, 3073, 3073,
3073, 3073, 2963, 2963, 2963, 2963, 2963, 2963, 2963, 2963,
2963, 2963, 2963, 2962, 2962, 2962, 2962, 2962, 2962, 2962,
2962, 2962, 2962, 2962, 2962, 2889, 2889, 2889, 2889, 2889,
2889, 2889, 2889, 2889, 2889, 2889, 2859, 2859, 2859, 2859,
2859, 2859, 2859, 2859, 2859, 2859, 2859, 2859, 2859, 2859,
2859, 2851, 2851, 2851, 2851, 2851, 2851, 2851, 2851, 2851,
2851, 2851, 2851, 2851, 2839, 2839, 2839, 2839, 2839, 2839,
2839, 2839, 2839, 2839, 2839, 2839, 2839, 2701, 2701, 2701,
2701, 2701, 2701, 2701, 2701, 2701, 2701, 2701, 2701, 2701,
2701, 2701, 2701, 2701, 2701, 2701, 2701, 2701, 2701, 2604,
2604, 2604, 2604, 2604, 2604, 2604, 2604, 2604, 2604, 2604,
2604, 2583, 2583, 2583, 2583, 2583, 2583, 2583, 2583, 2583,
2583, 2583, 2583, 2578, 2578, 2578, 2578, 2578, 2578, 2578,
2578, 2578, 2578, 2578, 2578, 2578, 2578, 2578, 2578, 2578,
2578, 2478, 2478, 2478, 2478, 2478, 2478, 2478, 2478, 2478,
2478, 2478, 2478, 2478, 2478, 2478, 2478, 2478, 2478, 2478,
2478, 2478, 2478, 2478, 2478, 2478, 2478, 2478, 2478, 2478,
2478, 2478, 2478, 2478, 2478, 2478, 2478, 2478, 2478, 2478,
2478, 2478, 2478, 2478, 2478, 2478, 2478, 2478, 2478, 2478,
2478, 2478, 2478, 2478, 2478, 2478, 2478, 2478, 2478, 2478,
2478, 2478, 2478, 2478, 2478, 2478, 2478, 2431, 2431, 2431,
2431, 2431, 2431, 2431, 2431, 2431, 2431, 2431, 2369, 2369,
2369, 2369, 2369, 2369, 2369, 2369, 2369, 2369, 2369, 2341,
2341, 2341, 2341, 2341, 2341, 2341, 2341, 2341, 2341, 2209,
2209, 2209, 2209, 2209, 2209, 2209, 2209, 2209, 2209, 2209,
2209, 2074, 2074, 2074, 2074, 2074, 2074, 2074, 2074, 2074,
2074, 2074, 2074, 2074, 2025, 2025, 2025, 2025, 2025, 2025,
2025, 2025, 2025, 2025, 2025, 1925, 1925, 1925, 1925, 1925,
1925, 1925, 1925, 1925, 1925, 1925, 1925, 1925, 1925, 1925,
1923, 1923, 1923, 1923, 1923, 1923, 1923, 1923, 1923, 1923,
1923, 1923, 1923, 1923, 1923, 1923, 1923, 1923, 1923, 1923,
1923, 1923, 1923, 1923, 1923, 1923, 1923, 1923, 1923, 1894,
1894, 1881, 1881, 1881, 1881, 1881, 1881, 1881, 1881, 1881,
1881, 1881, 1808, 1808, 1808, 1808, 1808, 1808, 1808, 1808,
1808, 1808, 1808, 1808, 1794, 1794, 1794, 1794, 1794, 1794,
1794, 1794, 1794, 1794, 1794, 1794, 1794, 1794, 1794, 1794,
1772, 1772, 1772, 1772, 1772, 1772, 1772, 1772, 1772, 1772,
1768, 1768, 1768, 1768, 1768, 1768, 1768, 1768, 1768, 1768,
1768, 1761, 1761, 1761, 1761, 1761, 1761, 1761, 1761, 1680,
1680, 1680, 1680, 1680, 1680, 1680, 1680, 1680, 1680, 1680,
1680, 1680, 1680, 1680, 1680, 1680, 1680, 1680, 1680, 1671,
1671, 1671, 1671, 1671, 1671, 1671, 1671, 1671, 1671, 1671,
1671, 1671, 1671, 1671, 1625, 1625, 1625, 1625, 1625, 1625,
1625, 1625, 1625, 1625, 1625, 1625, 1625, 1612, 1612, 1612,
1612, 1612, 1612, 1612, 1612, 1612, 1612, 1612, 1612, 1612,
1612, 1612, 1612, 1612, 1592, 1592, 1592, 1592, 1592, 1592,
1592, 1592, 1515, 1515, 1515, 1515, 1515, 1515, 1515, 1515,
1515, 1515, 1515, 1504, 1504, 1504, 1504, 1504, 1504, 1504,
1504, 1504, 1504, 1504, 1504, 1504, 1495, 1495, 1495, 1495,
1495, 1495, 1495, 1495, 1495, 1495, 1495, 1489, 1489, 1489,
1489, 1489, 1489, 1489, 1489, 1489, 1489, 1489, 1483, 1483,
1483, 1483, 1483, 1483, 1483, 1483, 1483, 1483, 1483, 1477,
1477, 1477, 1477, 1477, 1477, 1477, 1477, 1474, 1474, 1471,
1471, 1447, 1447, 1447, 1447, 1447, 1447, 1447, 1447, 1447,
1447, 1447, 1443, 1443, 1443, 1443, 1443, 1443, 1443, 1443,
1443, 1443, 1443, 1435, 1435, 1435, 1435, 1435, 1435, 1435,
1435, 1435, 1435, 1431, 1431, 1431, 1431, 1431, 1431, 1431,
1431, 1431, 1431, 1417, 1417, 1417, 1417, 1417, 1417, 1417,
1417, 1417, 1417, 1417, 1403, 1403, 1403, 1403, 1403, 1403,
1403, 1403, 1403, 1403, 1403, 1403, 1403, 1373, 1373, 1373,
1373, 1373, 1373, 1373, 1373, 1373, 1373, 1373, 1373, 1373,
1362, 1362, 1362, 1362, 1362, 1362, 1352, 1352, 1352, 1352,
1352, 1352, 1352, 1352, 1352, 1352, 1352, 1337, 1337, 1337,
1337, 1337, 1337, 1337, 1337, 1337, 1337, 1337, 1335, 1335,
1335, 1335
)
), row.names = c(NA, -1000L), class = c(
"tbl_df",
"tbl", "data.frame"
))
# we don't appear to be doing a time series
# so let's simplify by just focusing on area
# in log base 10
d <- sort(log10(RandomF$area_ha))
# characteristic file size range in powers
# of ten
range(d)
#> [1] 3.125481 3.845408
# 16 is the number of bins reflected
# by hist(d)$breaks |> length()
# or use 20 to compare to results in
# Lehsten, V., de Groot, W. J., Flannigan, M.,
# George, C., Harmand, P., and Balzter, H. (2014),
# Wildfires in boreal ecoregions: Evaluating the power
# law assumption and intra-annual and interannual variations,
# J. Geophys. Res. Biogeosci., 119, 14–23, doi:10.1002/2012JG002252.
bins <- cut(d, breaks = 16)
# the mean burn area for each bin
bin_means <- tapply(d, bins, mean)
# number of observations within each bin
bin_counts <- tapply(d, bins, length)
# burn area within each bin
a <- bin_means * bin_counts
midpoint <- function(interval_string) {
# Remove parentheses and brackets
interval_string <- gsub("\\(|\\[|\\)|\\]", "", interval_string)
# Split the string into lower and upper bounds
bounds <- strsplit(interval_string, ",")[[1]]
# Convert the bounds to numeric values
lower_bound <- as.numeric(bounds[1])
upper_bound <- as.numeric(bounds[2])
# Calculate and return the midpoint
return(mean(c(lower_bound, upper_bound)))
}
marks <- sapply(attributes(a)$dimnames[[1]],midpoint)
attributes(marks) <- NULL
attributes(a)$dimnames[[1]] = marks
cfs <- as.numeric(attributes(a[which.max(a)])$names)
cfs
#> [1] 3.69
# data frame with burn area by size
b <- data.frame(
area = log10(a),
size = marks)
# Create the base plot
p <- ggplot(b, aes(x = size, y = area))
# Distribution of burn area by fire size
p <- p + geom_col()
# Add a normal distribution curve layer
p <- p + stat_function(fun = dnorm, args = list(mean = mean(b$size), sd = sd(b$size)), color = "red", size = 1)
#> Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
#> ℹ Please use `linewidth` instead.
#> This warning is displayed once every 8 hours.
#> Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
#> generated.
# Display the plot
p +
xlab("Fire size in hectares base 10") +
ylab("Burn area in 100 hectares") +
theme_minimal()
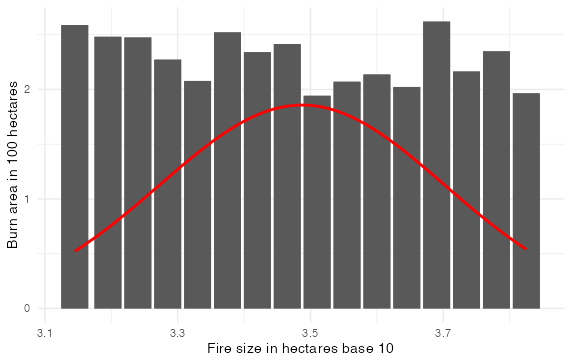
Created on 2023-10-22 with reprex v2.0.2