with these two functions:
t<-seq(0, 2*pi,0.01)
# splat curve
sp<- function(t) {
exp(1i*t) + (1+1i)*sin(6*t)^2
}
# figure of eight curve
figof8<- function(t) {
cos(t) + 1i*sin(2*t)
}
How can I get the following graph:
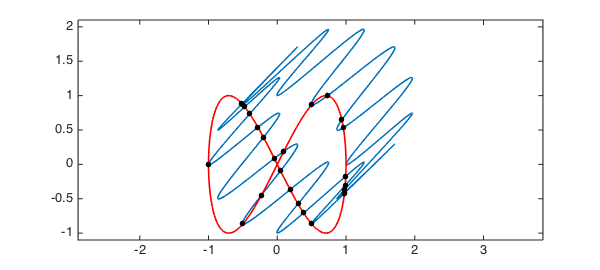
with these two functions:
t<-seq(0, 2*pi,0.01)
# splat curve
sp<- function(t) {
exp(1i*t) + (1+1i)*sin(6*t)^2
}
# figure of eight curve
figof8<- function(t) {
cos(t) + 1i*sin(2*t)
}
How can I get the following graph:

This should get you started
library('tidyverse')
d = tibble(t = t, y1 = sp(t), y2 = figof8(t)) %>%
gather(f, c, -t) %>%
mutate(x = Re(c), y = Im(c))
d %>%
ggplot(aes(x = x, y = y, colour = f)) +
geom_path() +
theme_bw()
and then you can e.g. use numerical approximation to find curve intersections in the complex plane
