Why are hyperparameters sample_size and learn_rate sampled across such a low range with Tidymodels using XGBoost?

[cwright1]

I've adapted some code from several public Tidymodels examples to setup an XGBoost model with hyperparameter tuning:

      # ____________________________________
      #Set up the model specification
      #The hyperparameters will be tuned
      xgb_spec <- 
        boost_tree(
        trees = 1000,
        tree_depth = tune(),
        min_n = tune(),
        loss_reduction = tune(),                    
        sample_size = tune(),
        mtry = tune(),   
        learn_rate = tune()) %>%
        set_engine("xgboost") %>%
        set_mode("regression")
      #____________________________________
      
      
      #____________________________________
      #Set up a space-filling grid design to cover the hyperparameter space as well as possible
      xgb_grid <-
        grid_latin_hypercube(
        tree_depth(),
        min_n(),
        loss_reduction(),
        sample_size = sample_prop(),
        finalize(mtry(), training_set), #gets treated differently b/c it depends on actual # of predictors in data
        learn_rate(),
        size = 40)
      #____________________________________

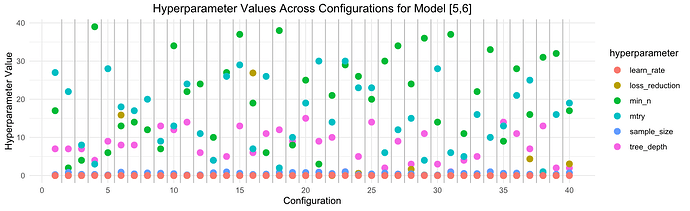
I understand that the grid_latin_hypercube here is supposed to use LHS to explore the hyperparameter space efficiently/uniformly, but I was confused to see that sample_size() is sampled over a range of ~0.1 to ~0.99, and loss_reduction from 1.5e-10 to ~2.

When plotting the 6 parameters' values across each of the 40 tested configurations, this is clear:

(ignore model name)

Is this as expected? Is this simply a function of not being able to put different parameters on the same scale, and if so, why are some sampled on different scales?

Thanks!

[Max]

Our default range for xgboost is [1/10, 1] for sample size and 10^[-10, 1.5] for loss reduction. Those are the defaults in dials.

We have to pick default ranges, which sometimes depend on the model being used. These are based on our experiences.

They are uniform but sometimes on a nonlinear scale (as with loss reduction above). This is sometimes because the range of values being several orders of magnitude necessitates a log scale (for example). Also, we know that for some parameters, a unit change on one side of the range has a very different effect than another part of the range and so on.

You can override these values using the update() method and change the parameters’ range and scale.