why (according to AIC) ETS(ANA) iseems to be a better method than ETS (ANN) in this particular case?

[Tony_iberian]

Example_2 aus_livestock from the Rob J Hyndman book

If the lowest AIC of two methodologies is considered to be the best metthod , I don´t undertand why for this data is showing that ETS (ANA) is a better method than ETS (ANN)?
it seems that there is no seasonality , when i look at ACF.
if there is no seasonility why is showing ETS (ANA) a better mehtod than ETS (ANN)
N = None?

ETS (ANN)
AIC AICc BIC
13737.10 13737.14 13750.07
ETS(A,N,A)
AIC AICc BIC
13545.38 13546.26 13610.24

8.8 Exercises | Forecasting: Principles and Practice (3rd ed)

Create variable

library("fpp3")
victoria_pigs <- aus_livestock %>% 
  filter(Animal =="Pigs",State == "Victoria") %>%
  view()

Simple exponential smoothing- Error Additive, No trend , No Seasonality

fit <- victoria_pigs%>%
  model(ETS(Count ~ error("A") + trend("N") + season("N")))

fit %>% 
report()

Simple exponential smoothing- Error Additive, No trend , Seasonility Additive

fit2 <- victoria_pigs%>%
  model(ETS(Count ~ error("A") + trend("N") + season("A")))

fit2 %>% 
report()

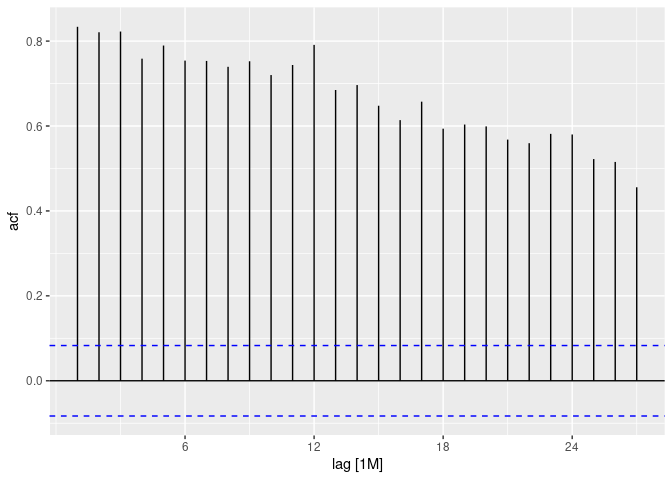
ACF Victorian pigs
victoria_pigs %>% 
  ACF(Count, lag_max = 36) %>% 
  autoplot()

[technocrat]

@Tony_iberian

it seems that there is no seasonality , when i look at ACF

There are additional tools to gauge seasonality. Also, I wouldn't put too much importance on the small difference between AIC for the two models.

library("fpp3")
#> ── Attaching packages ──────────────────────────────────────────── fpp3 0.4.0 ──
#> ✔ tibble      3.1.8     ✔ tsibble     1.1.1
#> ✔ dplyr       1.0.9     ✔ tsibbledata 0.3.0
#> ✔ tidyr       1.2.0     ✔ feasts      0.2.2
#> ✔ lubridate   1.8.0     ✔ fable       0.3.1
#> ✔ ggplot2     3.3.6
#> ── Conflicts ───────────────────────────────────────────────── fpp3_conflicts ──
#> ✖ lubridate::date()    masks base::date()
#> ✖ dplyr::filter()      masks stats::filter()
#> ✖ tsibble::intersect() masks base::intersect()
#> ✖ tsibble::interval()  masks lubridate::interval()
#> ✖ dplyr::lag()         masks stats::lag()
#> ✖ tsibble::setdiff()   masks base::setdiff()
#> ✖ tsibble::union()     masks base::union()
library(feasts)
victoria_pigs <- aus_livestock %>% 
  filter(Animal =="Pigs",State == "Victoria")
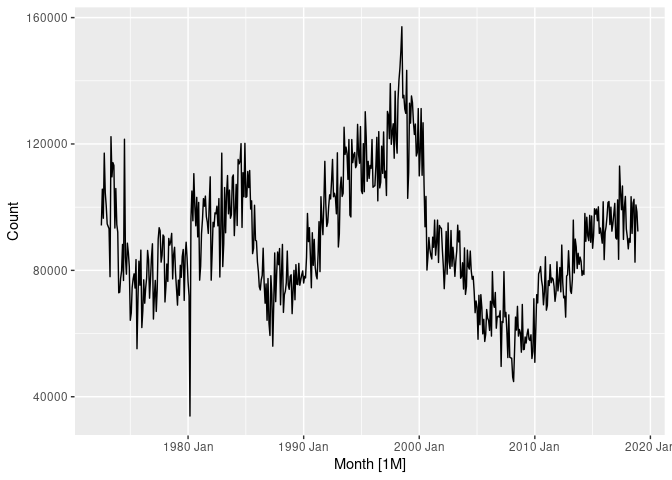
autoplot(victoria_pigs)
#> Plot variable not specified, automatically selected `.vars = Count`

victoria_pigs %>% features(Count, feat_stl)
#> # A tibble: 1 × 11
#>   Animal State   trend…¹ seaso…² seaso…³ seaso…⁴ spiki…⁵ linea…⁶ curva…⁷ stl_e…⁸
#>   <fct>  <fct>     <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>
#> 1 Pigs   Victor…   0.906   0.493       1       7 2.78e10 -46753. -97155.  -0.109
#> # … with 1 more variable: stl_e_acf10 <dbl>, and abbreviated variable names
#> #   ¹​trend_strength, ²​seasonal_strength_year, ³​seasonal_peak_year,
#> #   ⁴​seasonal_trough_year, ⁵​spikiness, ⁶​linearity, ⁷​curvature, ⁸​stl_e_acf1
#> # ℹ Use `colnames()` to see all variable names
victoria_pigs %>% unitroot_nsdiffs(Count)
#> nsdiffs 
#>       0
victoria_pigs %>% features(Count, feat_spectral)
#> # A tibble: 1 × 3
#>   Animal State    spectral_entropy
#>   <fct>  <fct>               <dbl>
#> 1 Pigs   Victoria            0.588
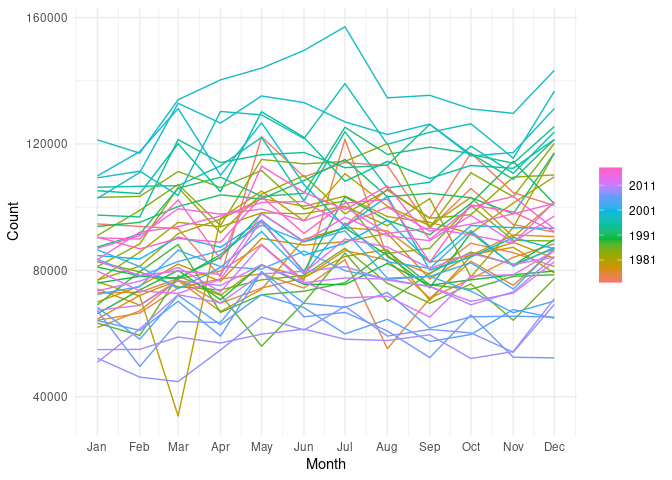
victoria_pigs %>% gg_season(Count)+ theme_minimal()

victoria_pigs %>% ACF(Count) %>% autoplot()

dcmp <- victoria_pigs %>%
  model(stl = STL(Count))
components(dcmp)
#> # A dable: 558 x 9 [1M]
#> # Key:     Animal, State, .model [1]
#> # :        Count = trend + season_year + remainder
#>    Animal State    .model    Month  Count   trend season_year remainder season…¹
#>    <fct>  <fct>    <chr>     <mth>  <dbl>   <dbl>       <dbl>     <dbl>    <dbl>
#>  1 Pigs   Victoria stl    1972 Jul  94200  97261.      12676.   -15736.   81524.
#>  2 Pigs   Victoria stl    1972 Aug 105700  97844.       4170.     3687.  101530.
#>  3 Pigs   Victoria stl    1972 Sep  96500  98426.      -3358.     1432.   99858.
#>  4 Pigs   Victoria stl    1972 Oct 117100  99009.       7701.    10390.  109399.
#>  5 Pigs   Victoria stl    1972 Nov 104600  99509.       4268.      824.  100332.
#>  6 Pigs   Victoria stl    1972 Dec 100500 100008.       4247.    -3755.   96253.
#>  7 Pigs   Victoria stl    1973 Jan  94700 100507.     -12361.     6554.  107061.
#>  8 Pigs   Victoria stl    1973 Feb  93900 100840.     -10139.     3199.  104039.
#>  9 Pigs   Victoria stl    1973 Mar  93200 101173.      -6261.    -1711.   99461.
#> 10 Pigs   Victoria stl    1973 Apr  78000 101505.      -8123.   -15382.   86123.
#> # … with 548 more rows, and abbreviated variable name ¹​season_adjust
#> # ℹ Use `print(n = ...)` to see more rows
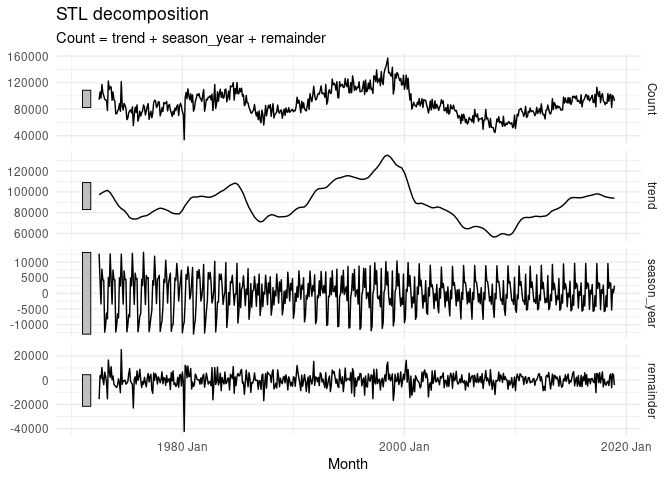
components(dcmp) %>% autoplot() + theme_minimal()

fit <- victoria_pigs%>%
  model(ETS(Count ~ error("A") + trend("N") + season("N")))

fit %>% 
  report()
#> Series: Count 
#> Model: ETS(A,N,N) 
#>   Smoothing parameters:
#>     alpha = 0.3221247 
#> 
#>   Initial states:
#>      l[0]
#>  100646.6
#> 
#>   sigma^2:  87480760
#> 
#>      AIC     AICc      BIC 
#> 13737.10 13737.14 13750.07

fit2 <- victoria_pigs%>%
  model(ETS(Count ~ error("A") + trend("N") + season("A")))

fit2 %>% 
  report()
#> Series: Count 
#> Model: ETS(A,N,A) 
#>   Smoothing parameters:
#>     alpha = 0.3579401 
#>     gamma = 0.0001000139 
#> 
#>   Initial states:
#>     l[0]     s[0]    s[-1]     s[-2]     s[-3]     s[-4]     s[-5]   s[-6]
#>  95487.5 2066.235 6717.311 -2809.562 -1341.299 -7750.173 -8483.418 5610.89
#>      s[-7]    s[-8]     s[-9]   s[-10]   s[-11]
#>  -579.8107 1215.464 -2827.091 1739.465 6441.989
#> 
#>   sigma^2:  60742898
#> 
#>      AIC     AICc      BIC 
#> 13545.38 13546.26 13610.24

[Tony_iberian]

many thanks!
what is feat_spectral and how do I Interpret it?

[technocrat]

See 4.4

• feat_spectral will compute the (Shannon) spectral entropy of a time series, which is a measure of how easy the series is to forecast. A series which has strong trend and seasonality (and so is easy to forecast) will have entropy close to 0. A series that is very noisy (and so is difficult to forecast) will have entropy close to 1.

[Tony_iberian]

@technocrat

feat_spectral will compute the (Shannon) spectral entropy of a time series, which is a measure of how easy the series is to forecast. A series which has strong trend and seasonality (and so is easy to forecast) will have entropy close to 0. A series that is very noisy (and so is difficult to forecast) will have entropy close to 1.

that´s fantastic many thanks!