When adding a confidence interval "manually", doesn't visually appear to cover most cases

Machine Learning and Modeling
1

[Edit since initial post]
I think I have a better understanding of what I am asking. I need to know how to make a prediction interval using nls() rather than a confidence interval. I would like to know how to do this manually.

I have a non linear regression model that is based on an exponential decay function. When I try to add a confidence interval, instead of using the models in built 'confidence interval' prediction, I wanted to do so manually. I get my model params and their standard errors, then calculate the prediction using the param +/- 2 standard errors. The plot I work on in the code below shows my final result. Expectation was to have a upper and lower confidence interval line encompassing most of the data, but instead it looks like it just passes through the middle :confused:

Example data:


library(tidyverse)
example_data <- dput(example_data)
structure(list(cohort_id = structure(c(1L, 1L, 1L, 1L, 1L, 1L, 
1L, 1L, 1L, 1L, 1L, 1L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 
2L, 2L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 4L, 4L, 
4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 5L, 5L, 5L, 5L, 5L, 5L, 
5L, 5L, 5L, 5L, 5L, 5L, 6L, 6L, 6L, 6L, 6L, 6L, 6L, 6L, 6L, 6L, 
6L, 6L, 7L, 7L, 7L, 7L, 7L, 7L, 7L, 7L, 7L, 7L, 7L, 7L, 8L, 8L, 
8L, 8L, 8L, 8L, 8L, 8L, 8L, 8L, 8L, 8L, 9L, 9L, 9L, 9L, 9L, 9L, 
9L, 9L, 9L, 9L, 9L, 9L, 10L, 10L, 10L, 10L, 10L, 10L, 10L, 10L, 
10L, 10L, 10L, 10L, 11L, 11L, 11L, 11L, 11L, 11L, 11L, 11L, 11L, 
11L, 11L, 11L, 12L, 12L, 12L, 12L, 12L, 12L, 12L, 12L, 12L, 12L, 
12L, 12L), levels = c("1", "2", "3", "4", "5", "6", "7", "8", 
"9", "10", "11", "12"), class = "factor"), billing_cycle = c(1L, 
2L, 3L, 4L, 5L, 6L, 7L, 8L, 9L, 10L, 11L, 12L, 1L, 2L, 3L, 4L, 
5L, 6L, 7L, 8L, 9L, 10L, 11L, 12L, 1L, 2L, 3L, 4L, 5L, 6L, 7L, 
8L, 9L, 10L, 11L, 12L, 1L, 2L, 3L, 4L, 5L, 6L, 7L, 8L, 9L, 10L, 
11L, 12L, 1L, 2L, 3L, 4L, 5L, 6L, 7L, 8L, 9L, 10L, 11L, 12L, 
1L, 2L, 3L, 4L, 5L, 6L, 7L, 8L, 9L, 10L, 11L, 12L, 1L, 2L, 3L, 
4L, 5L, 6L, 7L, 8L, 9L, 10L, 11L, 12L, 1L, 2L, 3L, 4L, 5L, 6L, 
7L, 8L, 9L, 10L, 11L, 12L, 1L, 2L, 3L, 4L, 5L, 6L, 7L, 8L, 9L, 
10L, 11L, 12L, 1L, 2L, 3L, 4L, 5L, 6L, 7L, 8L, 9L, 10L, 11L, 
12L, 1L, 2L, 3L, 4L, 5L, 6L, 7L, 8L, 9L, 10L, 11L, 12L, 1L, 2L, 
3L, 4L, 5L, 6L, 7L, 8L, 9L, 10L, 11L, 12L), sample_survival_rate = c(0.630375321185327, 
0.467011817658967, 0.365716219971609, 0.320696843452609, 0.289715829574683, 
0.274138331734878, 0.263859709445232, 0.257975988868186, 0.25428803817773, 
0.253349513689708, 0.251974683159173, 0.25087864807282, 0.626381321766971, 
0.457700237294344, 0.37100891459414, 0.322040406927193, 0.294130414649021, 
0.273224287881716, 0.264008524367158, 0.257890204475791, 0.254600100163038, 
0.252665019457592, 0.250872931127164, 0.249283495816814, 0.617466244254771, 
0.463682683415105, 0.371605156168376, 0.320962165438288, 0.294378622257423, 
0.272094922902315, 0.263553461969235, 0.258151398805649, 0.254228898501473, 
0.252721988646528, 0.250957888359671, 0.250678608369381, 0.625842284676012, 
0.475715043015969, 0.364457416055596, 0.326485932788029, 0.287971100886182, 
0.272805038087397, 0.263982745776158, 0.258071343467853, 0.254782618390382, 
0.252538854336153, 0.251931200298009, 0.250189014687092, 0.614958361152235, 
0.474023154666957, 0.37790296469348, 0.321305725376115, 0.288431205767636, 
0.273448941036557, 0.265221683162653, 0.257977862090824, 0.254402493942438, 
0.252262229858011, 0.252482170616736, 0.250167038793874, 0.615276997378503, 
0.462251124297695, 0.379117488405097, 0.320048927623227, 0.286479327627075, 
0.277112140101815, 0.264517062972436, 0.257970078541396, 0.254324910083164, 
0.253199527200694, 0.250985688661134, 0.251435584163309, 0.626165857232067, 
0.457716584851464, 0.380706922662529, 0.32214396867372, 0.28725348189702, 
0.274217428106078, 0.262850951863544, 0.258008309979443, 0.253982997355457, 
0.252432836066219, 0.252955446219195, 0.250173801962517, 0.626248558471049, 
0.474358329360571, 0.369797644382662, 0.324484196652504, 0.292835709935179, 
0.274812679385776, 0.264902105112049, 0.257920928121361, 0.254293689364316, 
0.252094179645866, 0.25146035913424, 0.251382845450947, 0.619935506915612, 
0.472368360759675, 0.376906826285281, 0.322622472724279, 0.294056956175115, 
0.2762753843963, 0.263543866656661, 0.257911561154227, 0.254082172527871, 
0.252479306436864, 0.25092022041681, 0.25147680046597, 0.620940410953731, 
0.458684083447818, 0.367775959111921, 0.31955299117994, 0.290834501870578, 
0.273073930174107, 0.264099158034426, 0.258049918137067, 0.254097282656084, 
0.252593088721244, 0.251201515264958, 0.249725999038376, 0.6178781171174, 
0.480537380689229, 0.370305282109615, 0.321910535895373, 0.295165049355668, 
0.274898706563092, 0.264775605155201, 0.257970685836666, 0.254379583052875, 
0.25230912983428, 0.251323575117219, 0.250613209856686, 0.627625590735999, 
0.470453669107974, 0.361352411452518, 0.329163446065758, 0.293046687979046, 
0.275398723193211, 0.263940477049976, 0.257914465199765, 0.254451201344154, 
0.251946651930126, 0.251414402429264, 0.252082405269007)), row.names = c(NA, 
-144L), class = c("tbl_df", "tbl", "data.frame"))

The above block creates a data frame example_data. Here's a plot of the fields of interest:

survival_plot <- example_data |> 
  ggplot(aes(x = billing_cycle, y = sample_survival_rate, color = cohort_id)) +
  geom_line()
survival_plot

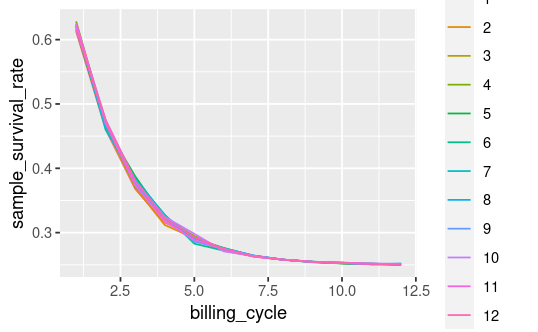
image

Then I fit a model. After fitting I retrieve the model params i, a and lambda along with their standard errors, then I (attempt to) add an upper and lower bound confidence interval:


mod.nls <- nls(sample_survival_rate ~ 
                 exponential_decay(i, a, lambda, billing_cycle), data = example_data, start = list(i = 0.5, a = 0.5, lambda = 0.15))

mod_summary <- mod.nls |> summary()

mod_i <- coef(mod.nls)['i']
mod_i_se <- mod_summary$coefficients["i", "Std. Error"]
mod_a <- coef(mod.nls)['a']
mod_a_se <- mod_summary$coefficients["a", "Std. Error"]
mod_lambda <- coef(mod.nls)['lambda']
mod_lambda_se <- mod_summary$coefficients["lambda", "Std. Error"]

# add 95% CI to example data
example_data <- example_data |> 
  mutate(
    mod_upper_ci = exponential_decay(mod_i + 2*(mod_i_se), mod_a + 2*(mod_a_se), mod_lambda + 2*(mod_lambda_se), billing_cycle),
    mod_lower_ci = exponential_decay(mod_i - 2*(mod_i_se), mod_a - 2*(mod_a_se), mod_lambda - 2*(mod_lambda_se), billing_cycle)
    )

But when I add the upper/lower interval to my plot I get this:

example_data |> 
  ggplot(aes(x = billing_cycle, y = sample_survival_rate, color = cohort_id)) +
  geom_line() +
  geom_line(aes(x = billing_cycle, y = mod_upper_ci), color = 'black') +
  geom_line(aes(x = billing_cycle, y = mod_lower_ci), color = 'black')

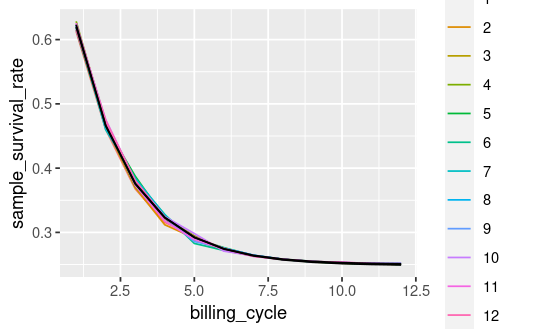
image

Does this look 'right'? I expected the black lines to encompass the cohort_ids, instead it looks like it's just going through the middle.

Is my approach flawed (presumably yes)? How can I correctly add a 95% confidence interval to my plot using the model params and their standard errors?

2

I think you made an assumption that the predictions with all coefficients moved down vs that with all moved up would span the widest range of the functions output, and it does not.

Here is a demonstration :

library(tidyverse)
# function
exponential_decay <- function(i, a, lambda, billing_cycle) i + a * exp(-lambda * billing_cycle)

# model params
i <- 0.25
i_se <- 0.001
a <- 0.65
a_se <- 0.001
lambda <- 0.55
lambda_se <- 0.02



# predictions as a base for sampling
predictions_df_1 <- data.frame(
  billing_cycle = 1:12
) |> 
  mutate(
    prediction = exponential_decay(i, a, lambda, billing_cycle),
    prediction_lower_ci = exponential_decay(i = i - 2 * i_se, a = a - 2 * a_se, lambda = lambda - 2 * lambda_se, billing_cycle),
    prediction_upper_ci = exponential_decay(i = i + 2 * i_se, a = a + 2 * a_se, lambda = lambda + 2 * lambda_se, billing_cycle)
  ) |> pivot_longer(-billing_cycle)

ggplot(predictions_df_1) + aes(x=billing_cycle,y=value,color=name) + geom_line()

predictions_df_2 <- data.frame(
  billing_cycle = 1:12
) |> 
  mutate(
    prediction = exponential_decay(i, a, lambda, billing_cycle),
    p_1 = exponential_decay(i = i - 2 * i_se, a = a + 2 * a_se, lambda = lambda + 2 * lambda_se, billing_cycle),
    p_2 = exponential_decay(i = i - 2 * i_se, a = a + 2 * a_se, lambda = lambda - 2 * lambda_se, billing_cycle),
    p_3 = exponential_decay(i = i - 2 * i_se, a = a - 2 * a_se, lambda = lambda + 2 * lambda_se, billing_cycle),
    prediction_lower_ci = exponential_decay(i = i - 2 * i_se, a = a - 2 * a_se, lambda = lambda - 2 * lambda_se, billing_cycle),
    prediction_upper_ci = exponential_decay(i = i + 2 * i_se, a = a + 2 * a_se, lambda = lambda + 2 * lambda_se, billing_cycle),
    p_6 = exponential_decay(i = i + 2 * i_se, a = a + 2 * a_se, lambda = lambda - 2 * lambda_se, billing_cycle),
    p_7 = exponential_decay(i = i + 2 * i_se, a = a - 2 * a_se, lambda = lambda + 2 * lambda_se, billing_cycle),
    p_8 = exponential_decay(i = i + 2 * i_se, a = a - 2 * a_se, lambda = lambda - 2 * lambda_se, billing_cycle),
  ) |> pivot_longer(-billing_cycle)

ggplot() + aes(x=billing_cycle,y=value,color=name) + 
  geom_line(data=predictions_df_2 |> filter(name %in% paste0("p_",1:8)),
            linetype="dashed"
  ) +
  geom_line(data=predictions_df_2 |> filter(! name %in% paste0("p_",1:8)),
            linetype="solid") +   theme(legend.position = "bottom")
4

Thanks for taking the time to answer Nir. I have modified my post, instead of showing how I created the data frame example_data, I have just pasted it using dput().

My question is about taking the standard errors of the model params, not the ones I had pasted initially.

Basically, I expected my 95% confidence interval to cover ~95% of cohorts on the final plot, but visually it does not.

Did I calculate the 95% CI incorrectly?

5

My post was trying to show how taking your 3 parameters, and setting them all -2, or all +2 does not give the widest extent, I think you will see from my chart which plots all combinations of -2/+2 combinations, that there are combinations with wider extent, and also this can vary over the curve.

One could perhaps collate all 8 possible curves, and for each point along the x axis pick the min and max bounds ?
or else another approach (though computationally expensive) might be to use bootstrapping to plot tens of thousands of variations of the curve based on the flexibility of the parameters, where each parameter is pulled from a distribution, and then see what the bounds are at different percentiles of those actual experiments, the moore bootstraps the better.