First, I'm not an expert on this topic: second opinion welcome!
Not exactly, in this chapter they are doing repeated 10-fold cross-validation, this is the number of replicates, but the number of folds is always 10.
One way to think about it is to consider 1-fold cross-validation. Let's say you have your data, you divide it into train and test. You leave the test set aside and never ever touch it to make a decision, you can always use it only once at the very end to estimate how good your final model is (estimate how well it generalizes to data it has never seen before). So you are left with your training set, and two different tasks: (i) you want to train the model (choose model parameters), and (ii) you want to select the best model among several models that you just trained (e.g. decide whether a random forest is doing better than logistic regression).
The simplest approach is to subdivide your training set in 2, one for the actual training, the other for the model selection. That would work, it's just not ideal. Another way is to take a single observation out, use all your training data to train, then do the model selection on that single value. Then take another value out, do the training with the rest, the selection on that last value. And so on for every single value. It means that for every single data point in your training set, you will do the whole training for every other value and evaluate your models on that single value. This approach works well, it is actually used in real life, but it's computationally intensive, since you're training all your models a lot of times.
So, an alternative way is to divide your training set in 10 (for example), train the models on 9/10th of the training set and compare them on the 10th set, and do that 10 times. You still get most of the benefit of cross-validation, but reducing the amount of computation a lot. But wait, when you divided initially your training set in 10 subsets, these subsets were random, you could have chosen different ones. So you can simply re-do a second subdivision of the training set into 10 new subsets. Then re-run the cross-validation procedure a second time (with 10 trainings and model comparisons). And why not do it a third time then? And a fourth? etc...
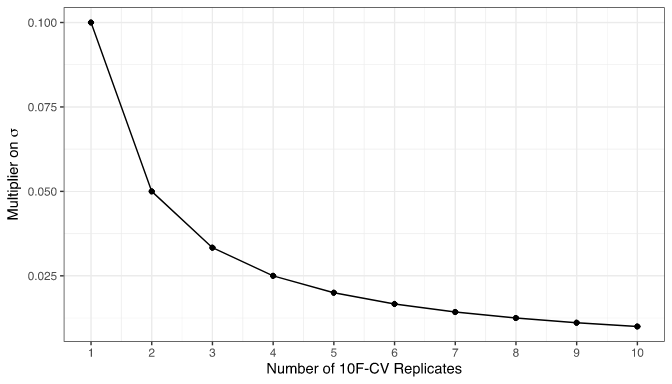
So in that case, you're doing repeated cross-validation; at each cross-validation you divide your training sample in V=10 folds, but you repeat that any number of times. What do you gain by repeating more cross-validations? That's what appears on the figure: the y-axis reflects the error on the result, if you just run a 1-fold cross-validation you get the leftmost point, but if you re-run the whole 10-fold cross-validation procedure several times you can further decrease that error.
Then, an interesting exercise could be to try to repeat the 10-fold cross-validation several times, OR to change the number of folds (the number of subsets made from the training set). You could try that on the Ames data and see which one is more efficient.
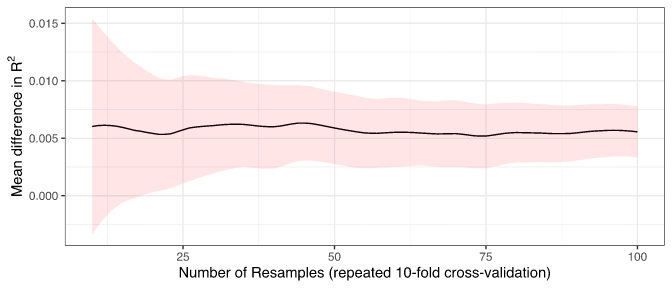
As to the figure from Chapter 11.3, this reflects something similar to chapter 10.2 (but they don't plot the same thing). The key sentence is this:
credible intervals with up to 100 resamples (generated from 10 repeats of 10-fold cross-validation)
So the corresponding command is:
vfold_cv(train, v = 10,repeat = 10)
Or rather, they repeated that command with the same value of train, the same v=10, but using repeat=1, then repeat=2, and so on until repeat=10. Since each repeat is already making 10 resamples (10 folds, and training the models 10 times on the other 9/10th folds), in total the models will have been trained 100 times on 100 different subsamples (each being a fold in a repeat).
And the interpretation is that the estimate of the parameter ("mean difference in R2") doesn't change too much with resamples, but the error/uncertainty on this estimate decreases in a way similar to the figure in 10.2: you gain a lot by repeating the 10-fold CV 3 times (i.e. 30 resamples), you don't gain much precision when going from 7 to 10 repeats of 10-fold CV, which is what you see in the figure from 10.2.