Exactly, ~3000 obs.
So I tried with a Kolmogorov–Smirnov test and even with a Lilliefors test, but result are still not even close from a normal distribution ... I don't know what to think.
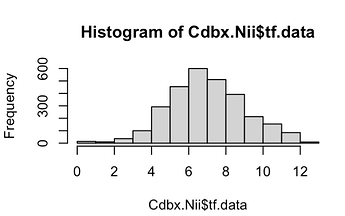
I made a few tests with ks.test() function. For remind, Cdbx.Nii is my transformed Nickel data, so it is almost normal, with this distribution:
> ks.test(Cdbx.Nii$tf.data, "pnorm",mean=mean(Cdbx.Nii$tf.data), sd=sd(Cdbx.Nii$tf.data))
One-sample Kolmogorov-Smirnov test
data: Cdbx.Nii$tf.data
D = 0.030362, p-value = 0.01007
alternative hypothesis: two-sided
I tried using others normal distribution (such as dnorm and qnorm) but p-value is < 2.2e-16.
Other example with a Lilliefors test:
> lillie.test(Cdbx.Nii$tf.data)
Lilliefors (Kolmogorov-Smirnov) normality test
data: Cdbx.Nii$tf.data
D = 0.030362, p-value = 2.126e-06