Trying to fit non linear regression and get the equation that describes the regression.

[eltef97]

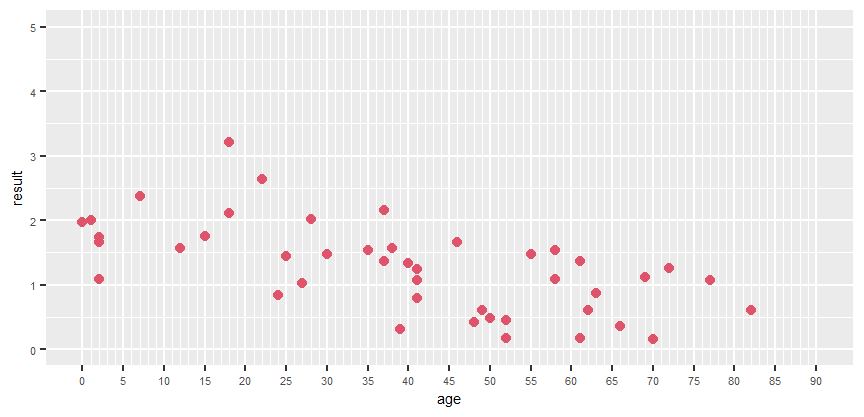
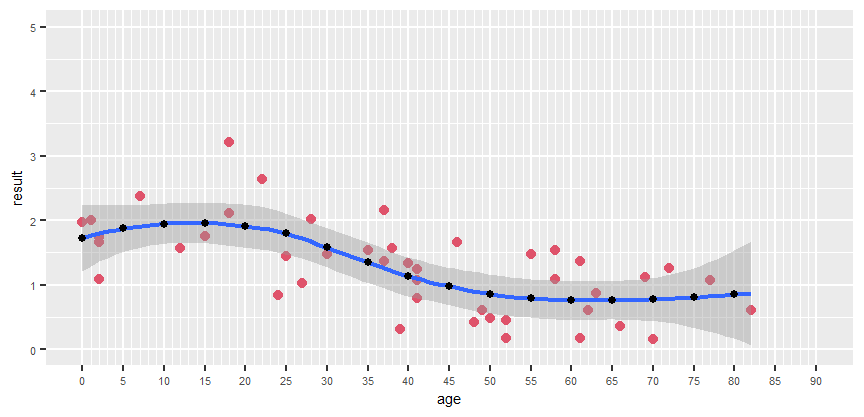
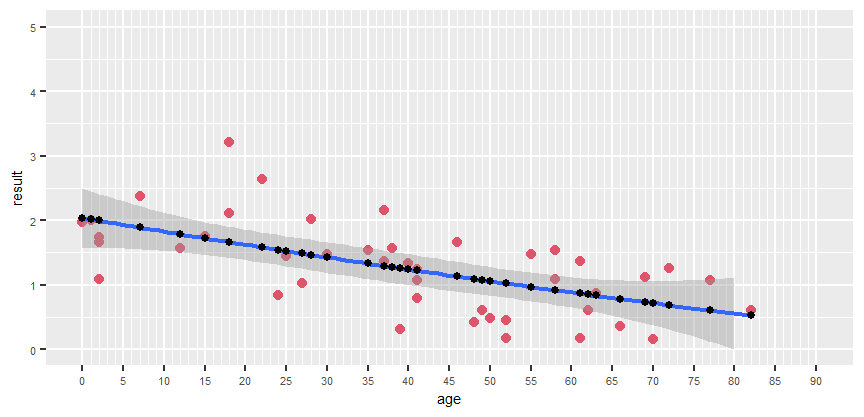
Hello. I'm having a bit of trouble with a visualisation, and i'm about as far from an expert as it gets when it comes to R. Any help would be much apreciated.

I have a set of data (3 actually) from experiments. Each has a set of values, and the ages of the experimental subjects. I have written a bit of code to help me visualise it in ggplot, and fit linear regression line. What is imporant, is that the x axis has to go from 0 to 90 showing each value even the ones for which i have no data. I probably should also note, that these values are averages, i actually have 3 values for each experiment, and i also wrote code to visualise in a boxplot dotplot form.

The problem is the following. I need to fit a non linear regression, and i need to know the equation for the regression line. This however seems to be difficult wihile maintaining the x axis as it is.

Here is my data and my code. Can anyone tell me what to do or how to get started? Thank you in advance!

library(ggplot2)
library(viridisLite)
library(tidyverse)
library(hrbrthemes)
library(viridis)
library(ggpubr)
library(nlme)

Fm_exp <- c(1.7434966, 1.0801409, 2.1167605, 3.2129330, 0.8309916, 2.0122389, 1.3666220, 1.3371467, 1.2490870, 1.6673520, 1.4810615, 1.0926890, 1.3596734, 0.6096441, 1.0759678)
H_1_exp <- c(1.9647631, 2.0084605, 1.5687817, 1.7500143, 2.6373049, 1.5306398, 2.1639198, 1.5670949, 1.0784589, 0.5986551, 0.1743043, 1.5402163, 0.8649401, 1.1173467, 1.2587116, 0.6119319)
T_1_exp <- c(1.6659381, 2.3747060, 1.4414554, 1.0302188, 1.4732338, 0.3131557, 0.7873363, 0.4274292, 0.4767390, 0.4514687, 0.1773119, 0.3509829, 0.1494075)

Ages_Hlty_Fm <- c(2, 2, 18, 18, 24, 28, 37, 40, 41, 46, 55, 58, 61, 62, 77)
Ages_Hlty_Ml <- c(0, 1, 12, 15, 22, 35, 37, 38, 41, 49, 52, 58, 63, 69, 72, 82)
Ages_Hlty_Mix <- c(2, 7, 25, 27, 30, 39, 41, 48, 50, 52, 61, 66, 70)

df_pre_1 <- data.frame(result=c(Fm_exp,H_1_exp,T_1_exp))
d_pre_2 <- c(Ages_Hlty_Fm,Ages_Hlty_Ml,Ages_Hlty_Mix)
df <- cbind(df_pre_1, age = factor(d_pre_2, levels = c(0:90)))

p <- ggplot(data = df, aes(x=age, y=result)) +
geom_point(data = df, aes(x=age, y=result), color="2", size=2) +
scale_x_discrete(drop = F) +
theme(text = element_text(size = 7)) +
ylim(0,5) +
p

[FJCC]

Would it work to make the x values numeric and use the breaks arguments to mark every integer?

Fm_exp <- c(1.7434966, 1.0801409, 2.1167605, 3.2129330, 0.8309916, 2.0122389, 1.3666220, 1.3371467, 1.2490870, 1.6673520, 1.4810615, 1.0926890, 1.3596734, 0.6096441, 1.0759678)
H_1_exp <- c(1.9647631, 2.0084605, 1.5687817, 1.7500143, 2.6373049, 1.5306398, 2.1639198, 1.5670949, 1.0784589, 0.5986551, 0.1743043, 1.5402163, 0.8649401, 1.1173467, 1.2587116, 0.6119319)
T_1_exp <- c(1.6659381, 2.3747060, 1.4414554, 1.0302188, 1.4732338, 0.3131557, 0.7873363, 0.4274292, 0.4767390, 0.4514687, 0.1773119, 0.3509829, 0.1494075)

Ages_Hlty_Fm <- c(2, 2, 18, 18, 24, 28, 37, 40, 41, 46, 55, 58, 61, 62, 77)
Ages_Hlty_Ml <- c(0, 1, 12, 15, 22, 35, 37, 38, 41, 49, 52, 58, 63, 69, 72, 82)
Ages_Hlty_Mix <- c(2, 7, 25, 27, 30, 39, 41, 48, 50, 52, 61, 66, 70)

df_pre_1 <- data.frame(result=c(Fm_exp,H_1_exp,T_1_exp))
d_pre_2 <- c(Ages_Hlty_Fm,Ages_Hlty_Ml,Ages_Hlty_Mix)
df <- cbind(df_pre_1, age = d_pre_2)

ggplot(data = df, aes(x=age, y=result)) +
  geom_point(data = df, aes(x=age, y=result), color="2", size=2) +
  scale_x_continuous(breaks = seq(0,90,5), limits = c(0,90),minor_breaks = seq(0,90)) +
  theme(text = element_text(size = 7)) +
  ylim(0,5) 

[eltef97]

Yes, that does work, using geom_smoothe, i do get a relatively good fitting. Thank you. I simply don't now how to get the equation, or modify the precision of what is fitted.

[FJCC]

Please show the code you are using to get the fit.

[eltef97]

library(stats)
library(ggplot2)
library(mgcv)

Fm_exp <- c(1.7434966, 1.0801409, 2.1167605, 3.2129330, 0.8309916, 2.0122389, 1.3666220, 1.3371467, 1.2490870, 1.6673520, 1.4810615, 1.0926890, 1.3596734, 0.6096441, 1.0759678)
H_1_exp <- c(1.9647631, 2.0084605, 1.5687817, 1.7500143, 2.6373049, 1.5306398, 2.1639198, 1.5670949, 1.0784589, 0.5986551, 0.1743043, 1.5402163, 0.8649401, 1.1173467, 1.2587116, 0.6119319)
T_1_exp <- c(1.6659381, 2.3747060, 1.4414554, 1.0302188, 1.4732338, 0.3131557, 0.7873363, 0.4274292, 0.4767390, 0.4514687, 0.1773119, 0.3509829, 0.1494075)

Ages_Hlty_Fm <- c(2, 2, 18, 18, 24, 28, 37, 40, 41, 46, 55, 58, 61, 62, 77)
Ages_Hlty_Ml <- c(0, 1, 12, 15, 22, 35, 37, 38, 41, 49, 52, 58, 63, 69, 72, 82)
Ages_Hlty_Mix <- c(2, 7, 25, 27, 30, 39, 41, 48, 50, 52, 61, 66, 70)

df_pre_1 <- data.frame(result=c(Fm_exp,H_1_exp,T_1_exp))
d_pre_2 <- c(Ages_Hlty_Fm,Ages_Hlty_Ml,Ages_Hlty_Mix)
df <- cbind(df_pre_1, age = d_pre_2)

ggplot(data = df, aes(x=age, y=result)) +
geom_point(data = df, aes(x=age, y=result), color="2", size=2) +
scale_x_continuous(breaks = seq(0,90,5), limits = c(0,90),minor_breaks = seq(0,90)) +
theme(text = element_text(size = 7)) +
ylim(0,3) +
geom_smooth(method = "loess", span = 0.73)

To clarify, my purpose here is to estimate age based on the experimental result. I thought the simplest and most accurate method would be to fit a function, and with any Y value solve for X.

[FJCC]

The loess method of regression does not yield a simple regression function. Wikipedia has an article that explains the method and it particularly mentions the lack of a regression function in the Disadvantages section: Local regression - Wikipedia.
Here is some code that uses geom_smooth with both the "loess" and "lm" methods, using a second order polynomial in the "lm" case. I picked second order as a simple case. I manually replicated what geom_smooth does in both cases. The lm fit does give you a function for the regression, though with your data it seems a linear fit would be just as useful.
The "wiggliness" of the loess fit can be increased by reducing the value of the span argument. Using 0.25 makes a distinct difference. I would hesitate to do that with these data.

library(ggplot2)
Fm_exp <- c(1.7434966, 1.0801409, 2.1167605, 3.2129330, 0.8309916, 2.0122389, 1.3666220, 1.3371467, 1.2490870, 1.6673520, 1.4810615, 1.0926890, 1.3596734, 0.6096441, 1.0759678)
H_1_exp <- c(1.9647631, 2.0084605, 1.5687817, 1.7500143, 2.6373049, 1.5306398, 2.1639198, 1.5670949, 1.0784589, 0.5986551, 0.1743043, 1.5402163, 0.8649401, 1.1173467, 1.2587116, 0.6119319)
T_1_exp <- c(1.6659381, 2.3747060, 1.4414554, 1.0302188, 1.4732338, 0.3131557, 0.7873363, 0.4274292, 0.4767390, 0.4514687, 0.1773119, 0.3509829, 0.1494075)

Ages_Hlty_Fm <- c(2, 2, 18, 18, 24, 28, 37, 40, 41, 46, 55, 58, 61, 62, 77)
Ages_Hlty_Ml <- c(0, 1, 12, 15, 22, 35, 37, 38, 41, 49, 52, 58, 63, 69, 72, 82)
Ages_Hlty_Mix <- c(2, 7, 25, 27, 30, 39, 41, 48, 50, 52, 61, 66, 70)

df_pre_1 <- data.frame(result=c(Fm_exp,H_1_exp,T_1_exp))
d_pre_2 <- c(Ages_Hlty_Fm,Ages_Hlty_Ml,Ages_Hlty_Mix)
df <- cbind(df_pre_1, age = d_pre_2) #factor(d_pre_2, levels = c(0:90))

#Manual LOESS fit and predicted values
FIT <- loess(result ~ age, data = df, span = 0.75)
LoessFit <- predict(FIT, newdata = data.frame(age = seq(0,80,5)))
LoessDF <- data.frame(age = seq(0,80,5), Fitted = LoessFit)

#Plot geom_smooth and points from manual LOESS fit
ggplot(data = df, aes(x=age, y=result)) +
  geom_point(color="2", size=2) +
  geom_smooth(formula = y~x, span = 0.75, method = "loess") +
  geom_point(aes(y = Fitted), data = LoessDF, color = "black") +
  scale_x_continuous(breaks = seq(0,90,5), limits = c(0,90),minor_breaks = seq(0,90)) +
  theme(text = element_text(size = 7)) +
  ylim(0,5) 

#Second order polynomial fit using either predict() or done manually
#The columns Fitted_poly and Fitted_poly2 are practically identical.
#The difference is due to limited precision in tyyping the manual coef.
Poly_Fit <- lm(result~poly(age,2, raw = TRUE), data = df)
Poly_Fit
df$Fitted_poly <- predict(Poly_Fit)
df$Fitted_poly2 <- 2.036 - 0.02142 * df$age + 3.678e-05 * (df$age)^2

ggplot(data = df, aes(x=age, y=result)) +
  geom_point(data = df, aes(x=age, y=result), color="2", size=2) +
  geom_smooth(formula = y~poly(x,2), method = "lm") +
  geom_point(aes(y = Fitted_poly), color = "black") +
  scale_x_continuous(breaks = seq(0,90,5), limits = c(0,90),minor_breaks = seq(0,90)) +
  theme(text = element_text(size = 7)) +
  ylim(0,5) 

[eltef97]

Thank you very much for all the help. I have other work to do today, but i will try it tomorrow and let you know how it went. Thanks again, i'm really out of my depth with this kind of thing.

[eltef97]

Hi. So i tried the code, and it seems to work well, i just think i'm probably misunderstanding something. If i use the predict function, i get Y values predicted. What i need is X values predicted. So if i input say 1, i get 1.76, which is the experimental value predicted for a 1 year old. Whereas what i want, is if i input 1 (the experimetnal value), i should get around 44 (the predicted age).

The reason a linear model is not optimal, is that i use this method for age determination. And as i get more and more data, the clearer it seems that the regression is not strictly linear, more sigmoid.

I'm sorry i'm asking for so much help, i'm sure inverting a predict function is trivial to most of you, but coding is very foreign to me.

[startz]

If you want to predict X values, regress X on Y rather than the other way around.

[Aaqib]

I think you are looking to get the equation thats working behind the scenes in case of geom_smooth, so basically you want the parameters found out by the fitted method so that you can use that on a new dataset, just like u get when using a simple lm() from which u can extract coefficients. I dont know if that works in case of a geom_smooth as the loess smoothing is a non-parametric method, and it doesn't have a simple equation like linear regression. It uses a local weighted regression to fit the data, and the degree of smoothness is controlled by the span parameter. u can predict however for the data not originally used as shown above by FJCC.