All of these work rather slick. I liked using mutate rather than cbind().
Here are data for timesteps 55, and 56.
transect <- structure(data.frame(Y = c(1000:0),
Z_55 = c(2201.3, 2204.7, 2201.3, 2204.7, 2201.3, 2204.6, 2201.3, 2204.6,
2201.3, 2204.6, 2201.4, 2204.6, 2201.5, 2204.6, 2201.6, 2204.7,
2201.8, 2204.8, 2202, 2204.9, 2202.2, 2204.5, 2202.5, 2204.7,
2202.9, 2205.1, 2203.3, 2205.3, 2203.7, 2205.3, 2204.2, 2203.7,
2204.7, 2203, 2205.2, 2201.2, 2199.5, 2196.5, 2199, 2197.1, 2202.7,
2196.3, 2191.5, 2179.7, 2165.3, 2161, 2168.4, 2156.7, 2164.4,
2138.4, 2109.8, 2086.5, 2046.4, 2049, 2067.8, 2051.6, 2076.9,
2080.5, 2113.5, 2092.8, 2082.1, 2049.2, 2004.2, 1965.7, 1898.6,
1905, 1914.7, 1940.1, 2000, 1990.2, 1990.2, 1950.8, 1898, 1852.6,
1774.3, 1793.6, 1825.9, 1834.4, 1890.9, 1874.2, 1867.2, 1823.7,
1762.9, 1713.7, 1606.9, 1618.3, 1557.1, 1595.3, 1655.5, 1639.7,
1686.3, 1635.9, 1583, 1521.6, 1417, 1455.3, 1518.5, 1512.4, 1582.1,
1566.5, 1606.8, 1528.1, 1528.3, 1443.5, 1384.9, 1355.5, 1286.2,
1230.9, 1118.2, 1164.5, 1229.7, 1209.3, 1276.6, 1226.8, 1204.1,
1151.6, 1073.1, 1004.9, 891.5, 935.5, 1009.7, 992.4, 1065.1,
1024.7, 1022.9, 969.5, 899.6, 848.7, 725.9, 755.1, 682.3, 711.7,
641.6, 671.1, 602.6, 632.8, 566.3, 597.3, 534.1, 564.1, 503.1,
530.8, 472.2, 492.9, 442.6, 488.2, 545.5, 539.7, 586.8, 564.9,
527.3, 527.2, 466.2, 501.6, 494.6, 484.6, 461.6, 466.6, 452.4,
442.5, 406.8, 406.8, 395.9, 386.8, 360.7, 362.4, 332.2, 313.4,
251.6, 289.6, 283.3, 270.4, 215.1, 262.6, 268.3, 271, 243.8,
232.4, 187.5, 212.9, 205.7, 196.5, 158.2, 188.4, 188, 186.2,
150.4, 173.1, 163.5, 158.6, 124.8, 146.3, 140.5, 134.4, 104.8,
124.4, 121.4, 116.9, 91.2, 107.8, 105.1, 103, 81.8, 95.4, 91.2,
89.4, 71.5, 82.9, 79.3, 77.8, 63, 72.1, 69.1, 67.8, 55.6, 63,
60.3, 59, 48.9, 51.9, 47.3, 44.5, 35.9, 36.9, 33.7, 33.7, 32.1,
31.7, 30.6, 30.5, 29.5, 29.4, 28.3, 28.2, 27.2, 27.1, 26.3, 26.2,
25.2, 25.3, 24.3, 24.4, 23.5, 23.8, 23.2, 23.4, 22.5, 22.9, 22.2,
22.8, 22.2, 22.7, 21.9, 22.4, 21.5, 22.3, 21.7, 22.4, 21.8, 23,
24.5, 23.7, 24.7, 23.7, 24.4, 23.6, 23.8, 24.1, 25.7, 24.5, 24.7,
24.7, 26.2, 25.3, 26.4, 25.7, 26.8, 26.6, 28.1, 27.6, 28.7, 29,
30.5, 29.9, 29.9, 31.2, 32.8, 33.4, 34.5, 35, 35.7, 36.1, 36.8,
37, 37.5, 37.9, 38.4, 39.1, 39.6, 40.4, 41, 41.8, 42.4, 43.3,
43.8, 44.8, 45.3, 46.7, 47.9, 48.4, 49.8, 49.8, 50.8, 51.7, 53.3,
54.7, 57, 58, 60, 60.5, 61.4, 62.1, 62.7, 62.9, 61.7, 64, 64,
66.9, 67.6, 71, 73, 74.1, 73.8, 72.4, 67.3, 69.8, 67.2, 74.3,
78, 81.1, 82.9, 84.4, 86, 85.8, 85.8, 87.5, 87.7, 89.6, 89.7,
91.6, 91.3, 94.1, 93.5, 97.8, 100.1, 102.8, 104.1, 104.5, 101.7,
105.1, 103.8, 107.3, 108.2, 111.1, 111.6, 115.8, 115, 119.7,
123, 125, 129.4, 132.1, 133.8, 135.9, 131.4, 140.5, 149.4, 148.9,
155, 155.6, 160.1, 160.2, 163.1, 161, 161.1, 160.7, 161.5, 162.2,
163.2, 166.1, 169, 173, 177.2, 177.9, 180.8, 175.7, 173.3, 175.7,
181.8, 181.2, 185.8, 185.4, 189.5, 189.8, 194, 195.5, 199.7,
200.8, 202.9, 203.5, 203.8, 205.6, 207.7, 209.1, 212.6, 211.6,
211, 209.8, 205, 208.3, 206.3, 210.4, 209.6, 209.6, 205.9, 208.6,
207.3, 211.8, 215.7, 216.9, 223.7, 220.3, 219.5, 228, 233.1,
245.1, 257.2, 257.5, 267.8, 268.5, 283.3, 289.2, 303.4, 299.4,
296.9, 290.5, 279.3, 281.2, 271.5, 280.6, 278.4, 286.6, 281.7,
294.4, 284.6, 300.9, 287.4, 313.1, 335.5, 340.7, 380.3, 371,
412.8, 390.4, 430.6, 375.8, 327.4, 353.1, 354.6, 394.7, 394.3,
464, 440.4, 504.9, 503.5, 568.1, 581.8, 654.3, 659.9, 719.1,
720.4, 766.6, 764.8, 806.7, 807.6, 850.3, 864.9, 916.5, 950,
1021, 1076.8, 1106.2, 1125.3, 1171, 1213.4, 1254.3, 1299.3, 1294.3,
1255.9, 1357.1, 1379.3, 1555, 1683.1, 1875.1, 2113.3, 2143, 2387.8,
2262.7, 2403, 2169.5, 2176.1, 1900.3, 1914.1, 1588.1, 1540.2,
1206.6, 1095.7, 781.7, 516, 410.1, 237.4, 252.8, 158.1, 307.4,
367.8, 323.2, 288, 230.5, 185.5, 116.8, 59.4, 24.2, 28.2, -26.3,
-43.9, -50.3, -76.1, -68.5, -108.1, -98.2, -126.1, -115.5, -128.1,
-117.6, -107.7, -125.2, -121.6, -140.1, -136.8, -188.2, -224.7,
-373.3, -514, -760.4, -1005.4, -1316.7, -1626.7, -1608.6, -1587.7,
-1533.1, -1472.6, -1457.7, -1428.4, -1423.9, -1406.9, -1399.5,
-1388.2, -1382.1, -1370.8, -1367.8, -1354.9, -1357.3, -1354.9,
-1345.5, -1335.4, -1320.9, -1307.3, -1302.7, -1305, -1288.8,
-1272.5, -1252.6, -1227.1, -1169.7, -1111.7, -1089.8, -1068.5,
-1058.8, -1049.8, -1038.9, -1032.2, -1020.3, -1012, -966.3, -930.5,
-821, -726.6, -667.1, -612.7, -520.8, -430, -271.8, -116.5, -347.9,
-577.9, -891.2, -1198.6, -1192.7, -1181, -1177.1, -1164.5, -1161.6,
-1149.3, -1149.3, -1151.5, -1133.4, -1126.6, -1110.1, -1102,
-1095.4, -1099.1, -1081.6, -1070, -1058.1, -1042.2, -1036.3,
-1024.7, -1022.1, -1016.5, -1006.4, -1000.5, -986.7, -977.4,
-968.9, -961, -952.3, -945.7, -932.8, -925.7, -907.3, -893.6,
-888.2, -880.1, -872.4, -857.6, -855.5, -851.4, -841, -834.4,
-820.9, -806, -803.6, -796.8, -786, -770.2, -768.2, -765.5, -752.1,
-738.2, -740.6, -746.1, -725, -707.1, -701.3, -687.8, -686.4,
-679, -673.3, -669.8, -654.6, -642.4, -639.1, -636.5, -626.9,
-622.8, -612.4, -599.9, -599.9, -595.2, -585.5, -576.3, -567,
-559.6, -553.3, -551.9, -540.8, -531.2, -520.4, -508, -507.5,
-505.1, -493.9, -480.3, -475.8, -471.3, -465.5, -458, -455.8,
-450.2, -442.1, -432.9, -429.7, -425.7, -419.3, -413.5, -409.3,
-407.6, -399.5, -391.2, -386.5, -379.9, -372.8, -365.8, -360.2,
-353.7, -347.7, -341.8, -337.4, -336, -327.7, -320.4, -315.3,
-308.6, -304.4, -298.5, -295, -288, -285.5, -281.1, -275.7, -268.7,
-265.2, -258, -254.9, -247.5, -245.2, -238.5, -235.8, -228.9,
-226, -218.8, -216.2, -209.2, -207, -202.4, -198.7, -193.2, -190.7,
-186.5, -181.4, -176.4, -174.1, -173.6, -167.3, -163.9, -162.9,
-166.6, -158.2, -155.8, -150.3, -149.5, -143, -141.1, -134, -128.1,
-124.2, -118.8, -115.5, -112.1, -108.3, -105.1, -101.5, -99.1,
-97.6, -98.8, -92.6, -87.9, -85.3, -82.9, -80.3, -80.5, -73.9,
-69.5, -67.2, -65.5, -65, -67.4, -60.7, -56.9, -53.7, -50.7,
-50.9, -48.4, -48.6, -44.2, -44.7, -40.3, -43.1, -43.2, -39.4,
-36.2, -31.5, -27.6, -26.2, -24.6, -25.4, -27.9, -23.5, -19.2,
-17.7, -13.5, -12.4, -9.7, -10.7, -8.8, -11.5, -13.4, -8.9, -4.5,
-2.5, 1.2, 2.5, 3.9, 5, 5.4, 7.6, 8.3, 9.9, 9.9, 13.2, 16.2,
14.5, 16, 12.7, 11.3, 17.1, 21.8, 24.5, 27.6, 29.3, 31.4, 32.8,
34.2, 32.3, 27.8, 31, 31.9, 34.1, 35.1, 38.6, 44.1, 43.2, 47.9,
45.1, 50.1, 37.4, 22, 42.4, 53.7, 54.2, 53.7, 53.6, 55.6, 54.2,
54.3, 57.4, 60.7, 60.6, 62.1, 53.7, 43, 53.9, 63.8, 63.5, 64.8,
53.1, 43.6, 53.4, 65.4, 65.5, 65.6, 65.6, 65.9, 64.3, 61.4, 64.9,
66.8, 55.6, 34.4, 49.2, 48.2, 59.3, 64, 65.3, 65.2, 56.6, 37.9,
44.8, 37.2, 55.3, 68, 68.5, 68.8, 69.2, 69.3, 66.2, 59.8, 66.4,
69.9, 70.1, 70.2, 61.7, 49.8, 54.9, 50.6, 56.7, 50.8, 63.5, 70.1,
69.8, 69.1, 67.5, 63.5, 67.8, 70.1, 65.5, 70.1, 65.5, 70, 69.7,
70, 66.2, 69.9, 66.4, 69.7, 66.4, 60.3, 66.1, 69.1, 68.5, 67.5,
56.9, 39.3, 49.5, 46.3, 56.2, 65.8, 62.1, 63.4, 61.9, 65.7, 63.5,
67.9, 67.9, 67.9, 67.3, 67.5, 67.2, 67.7, 63.3, 67.5, 62.8, 66.4,
58.9, 50.6, 58.4, 66.2, 66.5, 67.3, 66.7, 65.7, 66.2, 67.2, 60.6,
49.6, 56.6, 54.7, 62.3, 66.2, 61.5, 54.9, 61.4, 66, 65.7, 65.6,
65.2, 64.9, 58.1, 45.4, 57.6, 63.9, 63.5, 63.1, 62.8, 62.8, 62.3,
62, 55.2, 47.1, 53.1, 62),
Z_56 = c(2212.2, 2215.6, 2212.2, 2215.5, 2212.2, 2215.5, 2212.2, 2215.5,
2212.3, 2215.5, 2212.3, 2215.5, 2212.4, 2215.6, 2212.6, 2215.7,
2212.7, 2215.8, 2213, 2215.9, 2213.2, 2216.1, 2213.6, 2216.3,
2213.9, 2216.2, 2214.4, 2215.6, 2214.8, 2215.8, 2215.3, 2216.6,
2215.9, 2216.9, 2216.5, 2214.9, 2212.3, 2210.2, 2212.3, 2209.2,
2214.8, 2205.9, 2203.5, 2197.4, 2201.3, 2198.4, 2207.1, 2195,
2185.7, 2166.1, 2142.7, 2136.6, 2148.3, 2130.4, 2141, 2102.8,
2058.4, 2037.4, 1986.1, 2003, 2033.9, 2014.2, 2042.9, 2047.1,
2084.6, 2058.2, 2041.1, 2007.1, 1957, 1911.9, 1833.8, 1851.3,
1877.7, 1892.1, 1951.5, 1940, 1938.3, 1897.5, 1840.8, 1790.2,
1704, 1729.4, 1772.7, 1773.8, 1831.2, 1811.1, 1800, 1753.8, 1686.6,
1633.3, 1517.1, 1530.7, 1465.3, 1507.3, 1572.3, 1556.3, 1607.5,
1553.6, 1497.6, 1433, 1322.5, 1363.5, 1430.2, 1423, 1495.2, 1469.2,
1498.1, 1412.2, 1416.7, 1340.5, 1311.7, 1270, 1197.4, 1137.5,
1021.4, 1067.9, 1133.2, 1113, 1180.9, 1130.6, 1107.6, 1054.8,
975.7, 907.9, 795, 838.8, 912.5, 895.5, 967.7, 927.5, 925.3,
872.5, 803.1, 753.1, 632.1, 661.4, 590.4, 619.7, 551.8, 581,
515, 544.6, 481.1, 511.4, 451.4, 480.7, 423.6, 450.7, 397, 417.6,
373.1, 415, 466.3, 461.9, 504.1, 482.5, 446.4, 435.1, 359, 412,
415.1, 409.1, 387.1, 393.4, 378.6, 371.5, 336.5, 339.6, 327,
321.2, 294.4, 297.2, 268, 250.4, 194.5, 228.5, 223.2, 208.9,
160, 201.6, 208.5, 213.6, 190.2, 179.2, 138.3, 161.2, 155.7,
145.5, 111, 137.8, 139, 137.2, 104.5, 125.5, 117.5, 110.8, 80.8,
100, 97.8, 91.4, 66.2, 83, 82.1, 77, 55.6, 69.9, 69.1, 67.3,
49.7, 61.2, 58, 56.7, 42.1, 51.4, 48.3, 47, 34.9, 42.3, 39.9,
38.6, 28.5, 34.6, 32.8, 31.7, 23.5, 25.7, 22.3, 20.4, 14.8, 15.4,
12.9, 13, 11.5, 11.3, 10.4, 10.4, 9.6, 9.6, 8.7, 8.7, 7.9, 8,
7.4, 7.5, 6.7, 6.9, 6.1, 6.4, 5.7, 6.2, 5.7, 6.1, 5.4, 6.1, 5.6,
6.4, 6, 6.7, 6.1, 6.8, 6.1, 7.2, 6.8, 7.7, 7.4, 8.8, 10.5, 9.9,
11.1, 10.4, 11.4, 10.8, 11.2, 11.8, 13.6, 12.6, 13.1, 13.3, 15.1,
14.4, 15.7, 15.3, 16.6, 16.7, 18.5, 18.2, 19.6, 20, 21.9, 21.5,
21.8, 23.3, 25.2, 25.7, 26.3, 27.3, 27.9, 28.9, 29.7, 30.6, 31.3,
32, 32.8, 33.6, 34.5, 35.4, 36.3, 37.2, 38.2, 39.2, 40.2, 41.1,
42.3, 43.1, 44.2, 45.1, 46.5, 47, 48.7, 49.5, 51.7, 52.9, 55.8,
56.5, 58.8, 59.5, 61.2, 61.9, 62.9, 63.2, 62.6, 64.4, 64, 66.8,
66.9, 70.9, 72.7, 75.2, 75.9, 75.5, 71.7, 74.3, 72.1, 78.4, 81.6,
84.1, 84.8, 87.7, 89.6, 91.1, 92.5, 93.9, 94.9, 96.3, 97.2, 98.8,
99.3, 101.7, 101.9, 105.9, 108.9, 109.6, 109.3, 112, 111.4, 114.6,
113.9, 117.2, 118.7, 121.1, 122.5, 125.3, 125.2, 127.8, 127.9,
132.9, 137.9, 140.4, 142.7, 143.5, 138.9, 147.8, 155.6, 155.6,
162.4, 162.6, 168.4, 168.5, 173.3, 171.6, 174.5, 174.1, 175.9,
176.3, 177.8, 179.2, 181.2, 184.7, 188.7, 190, 193.4, 189.8,
188.8, 190, 194, 193.4, 196.7, 196.5, 200.4, 201.2, 206.2, 207.2,
211.8, 213.4, 216.8, 217.1, 218.3, 219.2, 221.5, 222.4, 225.8,
225.3, 225.6, 224.6, 221.4, 223.6, 222.2, 225.1, 224.4, 224.8,
222.5, 224.5, 223.8, 226.5, 228.5, 230, 235.2, 232.3, 231.6,
238.3, 242.6, 252.7, 262.3, 264, 273.2, 273.7, 286.2, 290.9,
303.8, 301.4, 301.5, 296.3, 289.5, 288.5, 280.5, 286.6, 284,
292.6, 292.8, 301.2, 294.9, 306.5, 297, 316.5, 332.4, 335.3,
360.6, 354.5, 383.3, 367.8, 396.3, 360.6, 330.4, 351.3, 354.3,
371, 356.9, 401.6, 371.4, 419.3, 408, 465.7, 462.6, 544.6, 533.4,
617, 613.5, 687.2, 692.7, 751.4, 760.4, 808, 824.8, 873, 899.9,
962.5, 1008.5, 1019.1, 1022.4, 1058.3, 1092.6, 1128.1, 1166,
1151.6, 1096.7, 1197.7, 1217, 1335.9, 1383.8, 1591.5, 1812.5,
1820.1, 2023.9, 1915.6, 2063.8, 1797.8, 1804.3, 1469.9, 1498,
1118.4, 1126.4, 751.9, 708, 413.2, 197.4, 186.6, 132.4, 139.5,
125.6, 188.5, 218.9, 187.1, 165.4, 127, 97.5, 57.3, 23.5, -6.1,
0.6, -54.6, -73, -80.2, -106.8, -99.9, -140.3, -131.2, -159.8,
-150, -163.4, -153.6, -144.5, -162.7, -159.9, -179.1, -176.6,
-228.7, -266, -394.4, -514.8, -720.4, -924.5, -1194.8, -1463.8,
-1425.6, -1384.7, -1330.6, -1270.8, -1256.5, -1227.9, -1224,
-1207.5, -1200.7, -1190.1, -1184.6, -1173.9, -1171.4, -1159.1,
-1162, -1160.1, -1151.3, -1141.8, -1106.7, -1072.5, -1027, -988.1,
-930.6, -873, -832.9, -787.2, -729.8, -672.2, -650.7, -629.9,
-578.5, -527.7, -434.2, -344.6, -249.6, -158.4, 12.3, 173.1,
336.2, 476.9, 310.8, 128, 88.8, 38.7, -66.1, -178.6, -411.4,
-641.3, -956.7, -1264.4, -1265.2, -1265.5, -1249.9, -1233.1,
-1228.9, -1218.7, -1213.1, -1210, -1198.6, -1191, -1178.2, -1169,
-1158.7, -1156.8, -1149.1, -1149.4, -1127.7, -1106.4, -1100.6,
-1089.5, -1079.6, -1069.2, -1063.2, -1063.7, -1048.8, -1038.4,
-1030.6, -1022.6, -1014.4, -1006.2, -994.5, -985, -967.3, -950.8,
-946.2, -937.7, -931, -919.1, -915.2, -911.1, -900, -892.6, -878.8,
-862, -861.1, -854.5, -848.5, -841.5, -831.6, -825.8, -810.6,
-796.3, -792.9, -789.1, -774.7, -760, -754.2, -740.9, -739.5,
-730.5, -726.3, -721.7, -708.7, -694, -696.7, -702.3, -682, -673.5,
-662.2, -654.1, -649.3, -642.8, -634, -624.4, -612.2, -600.8,
-592.7, -584.3, -580.1, -572.4, -562.3, -549, -549.9, -548.4,
-537, -523.6, -518.4, -514.3, -507.5, -499.4, -497.2, -492.1,
-485.9, -481.1, -474.1, -467.4, -461.3, -455.4, -446.8, -438.7,
-432.3, -424.8, -417.9, -410.7, -406.6, -404.7, -395.9, -387.7,
-381.9, -374.5, -369.4, -363.1, -358.7, -351.2, -349.1, -344.8,
-337.8, -329.1, -325, -317, -312.3, -303.3, -301.2, -294.8, -291.5,
-283.9, -280.4, -272.5, -269.3, -261.6, -258.7, -253.6, -249.2,
-243, -239.9, -235.1, -229.4, -223.7, -220.8, -219.7, -212.8,
-208.7, -207.1, -210.2, -201.2, -198.2, -192.1, -190.7, -183.6,
-181.2, -173.4, -167, -162.5, -156.6, -152.7, -148.7, -144.3,
-140.6, -136.5, -133.5, -131.4, -132.1, -125.4, -120.2, -117.1,
-114.1, -111, -110.7, -103.6, -98.7, -95.9, -93.7, -92.7, -94.6,
-87.4, -83.2, -79.5, -76, -75.8, -72.8, -72.5, -67.7, -67.7,
-62.9, -65.2, -64.9, -60.7, -57, -51.9, -47.6, -45.7, -43.8,
-44.1, -46.3, -41.5, -36.8, -34.9, -30.3, -28.8, -25.8, -26.4,
-24.1, -26.4, -28, -23.1, -18.4, -16, -12, -10.4, -8.6, -7.1,
-6.5, -4, -2.9, -1.1, -0.7, 1.8, 4, 2.9, 4.1, 2.1, 1.7, 5.7,
8.8, 11.2, 13.5, 16, 17.8, 20.3, 20.9, 18.9, 11.6, 16.7, 16.3,
20.7, 20.9, 27.4, 33.6, 33.4, 39, 36.4, 41.8, 31.6, 18.5, 36.6,
46.5, 47.3, 46.3, 47.2, 48.1, 49.4, 50.8, 53.9, 56.6, 57.4, 59.1,
51.8, 42.1, 52.6, 61.5, 61.8, 63.1, 52.3, 43.6, 53.5, 65.7, 65.9,
66.2, 66.3, 66.8, 65.2, 62.5, 66.1, 68.2, 57, 35.9, 50.9, 49.9,
61.2, 66, 67.4, 67.4, 58.8, 40.3, 47.3, 39.8, 57.9, 70.7, 71.3,
71.7, 72.2, 72.4, 69.3, 63, 69.7, 73.2, 73.5, 73.6, 65.2, 53.4,
58.6, 54.3, 60.5, 54.6, 67.3, 74, 73.8, 73.2, 71.6, 67.7, 72,
74.3, 69.8, 74.4, 69.9, 74.5, 74.2, 74.5, 70.8, 74.5, 71, 74.4,
71.1, 65, 70.8, 73.8, 73.3, 72.3, 61.7, 44.2, 54.3, 51.2, 61.1,
70.7, 67, 68.4, 66.9, 70.7, 68.5, 72.9, 73, 72.9, 72.4, 72.5,
72.3, 72.8, 68.5, 72.6, 68, 71.6, 64.1, 55.7, 63.6, 71.4, 71.7,
72.5, 71.9, 70.9, 71.4, 72.4, 65.8, 54.8, 61.9, 59.9, 67.5, 71.4,
66.8, 60.2, 66.6, 71.2, 70.9, 70.6, 70.4, 70.2, 63.4, 50.7, 62.8,
69.1, 68.7, 68.3, 68.1, 68.1, 67.5, 67.2, 60.5, 52.3, 58.3, 67.3
)))
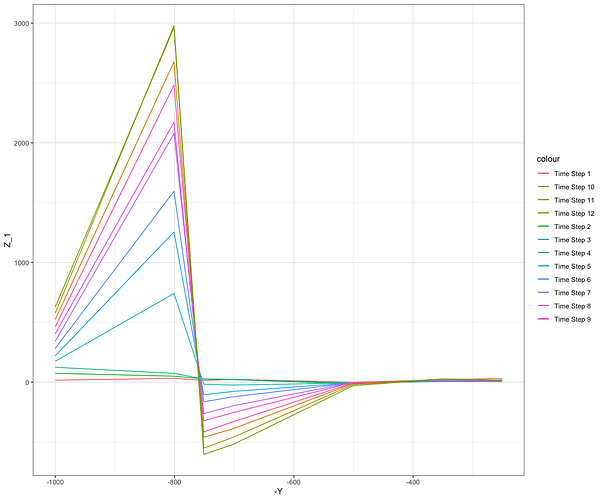
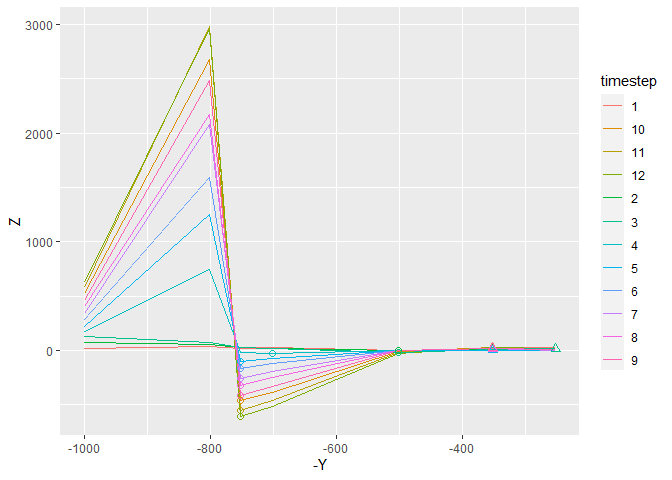
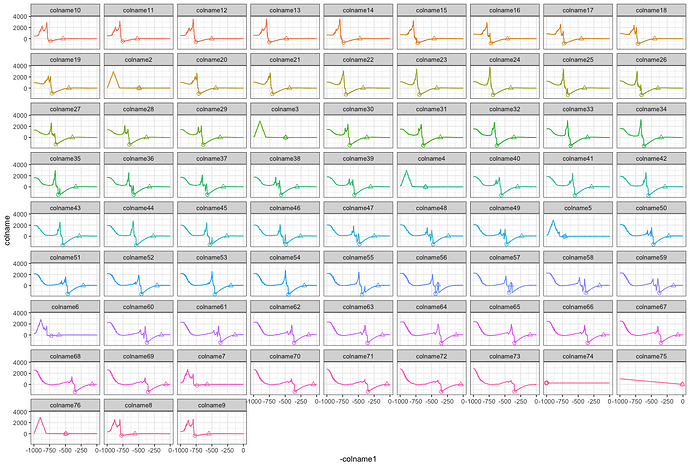
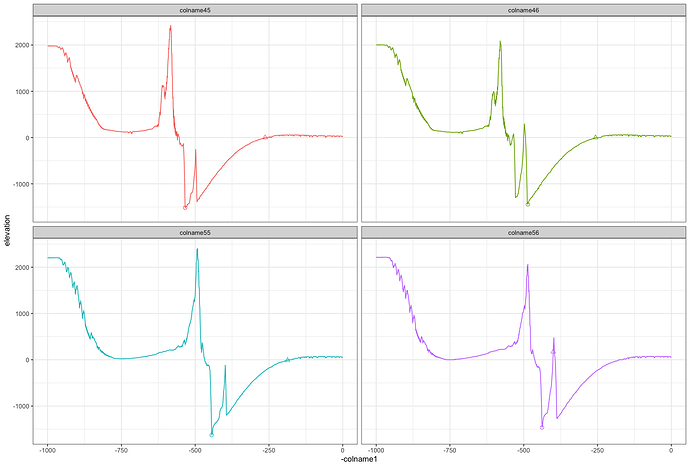
Essentially, my goal is that when second mountain (the peak in trough, ~ at 450-300 in plot 55 & 56 and ~550 - 400 in plots 45 & 46 on the Y-axis)grows above sea-level, the point of interest indicated by the circle will shift to the right of the second mountain. The point of interest indicated by the triangle will stay in the same place. This happens from plot 45 - 46.
In plots 55 - 56 the point of interest marked by the triangle jumps and the circle does not. In cases like 45, 46 and all others aside from 55 - 56, the min() logic was all that was needed to move the circle from one side of the mountain to the other. I believe the way you had the placement of Y_sea_level chosen depends upon the placement of Y_lowest_point, correct?