Should categorical and ordinal variables be converted to factors if their values are already numeric?

[karansehgal1988]

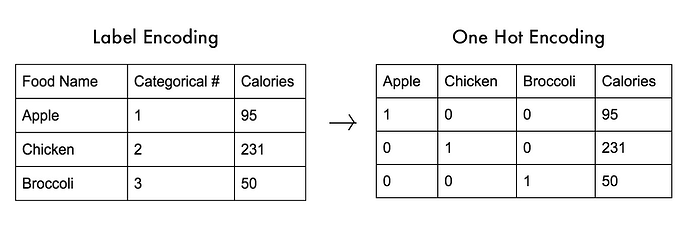
If the the categorical data is already given in numeric variable for like 1,2,3,4..... Then should we convert it into factor variable or should we convert it into dummy variable. What about the ordinal variables, do we need to convert them to factor variable for ordering them in right fashion before doing regression model ?

[pieterjanvc]

Hi,

Working with categorical and ordinal values in regression models is always a bit more complex than just numeric values.

Categorical variables
What you have to do is convert the categories to a one-hot vector, meaning that every category becomes a separate column in your data and then you set the column with the correct variable to 1 and all others to 0

Luckily, the glm function in R does that automatically when it detects a factor:

test = data.frame(z = sample(0:1, 50, replace = T), 
                  x = runif(50), 
                  y = sample(as.factor(1:5), 50, replace = T))
glm(z ~ x + y, data = test)

Call:  glm(formula = z ~ x + y, data = test)

Coefficients:
(Intercept)            x           y2           y3           y4           y5  
    0.19753      0.08841      0.46226      0.35903      0.12559      0.32568  

Degrees of Freedom: 49 Total (i.e. Null);  44 Residual
Null Deviance:	    12.48 
Residual Deviance: 11.28 	AIC: 81.42

Note how the categorical variable y (having 5 levels) becomes 4 different variables in the formula (the fifth one is all others set to 0)

If your categorical data is in numeric format, you have to make sure it's interpreted as a factor, or the glm will treat it as a numeric value (and don't create separate categories):

test = data.frame(z = sample(0:1, 50, replace = T), 
                  x = runif(50), 
                  y = sample(1:5, 50, replace = T))

Call:  glm(formula = z ~ x + y, data = test)

Coefficients:
(Intercept)            x            y  
    0.35930      0.35035      0.00695  

Degrees of Freedom: 49 Total (i.e. Null);  47 Residual
Null Deviance:	    12.42 
Residual Deviance: 11.93 	AIC: 78.26

So this is NOT what you want in case y is categorical

Ordinal variables
These variables have order, but the distance between them is not known, so it's between numeric and categorical. Again, you can specify a variable to be ordinal, an glm will make sure to take care of the rest:

test = data.frame(z = sample(0:1, 50, replace = T), 
                  x = runif(50), 
                  y = factor(sample(as.factor(1:5), 50, replace = T),
                             levels = as.factor(1:5), ordered = T))
glm(z ~ x + y, data = test)

Call:  glm(formula = z ~ x + y, data = test)

Coefficients:
(Intercept)            x          y.L          y.Q          y.C          y^4  
    0.42706     -0.05750     -0.08133     -0.28840      0.20110     -0.07878  

Degrees of Freedom: 49 Total (i.e. Null);  44 Residual
Null Deviance:	    12 
Residual Deviance: 10.76 	AIC: 79.07

Note that again the different ordinal values are split into separate columns, but now each one is represented by a polynomial function (again n - 1 functions). L, Q and C stand for Linear, Quadratic and Cubed respectively, 4 is a 4th degree polynomial and so on...

Hope this helps
PJ

[karansehgal1988]

Hi,

1. Regarding Ordinal Variables, we need to specify the order of the levels and why glm creates polynomial functions like L, Q, C and so on.... is that right to get created ? Will there not be any effect on the model.

2. Ordinal Variables when converted to Ordered factor variables in R and if some of the levels are insignificant in this ordered factor variable after we run the glm or lm function then how can we eliminate them from the glm or lm function?

3. Nominal Variables when converted to factor variables in R and if some of the levels are insignificant in this factor variable after we run the glm or lm function then how can we eliminate them from the glm or lm function?

Thanks,
Karan Sehgal