Residuals assumptions in glmm not verified! Help

[Alicem]

0

I am trying out GLMMs models to test whether two categorical variables (species and sex) and their interaction (sex + species + sex*species= fixed factors) influence certain acoustic parameters (response variable) of some vocalisations. My response variables are continuous numerical positive, such as the Fundamental frequency or duration of vocalizations. So, I'm trying different glmms for every acoustic parameter I have. My model has the ID as random factor, and the context of emission of vocalizations as another fixed variable. For each individual I have more than one observation, meaning that each individual vocalized more than once.

My response variables don't have a normal distribution, some of them are very asymmetrical, and one of them has two central humps. I have tried for example with the fundamental frequency, I've done a logarithmic transformation and used gamma, gaussian or inverse.gaussian with various link functions (log, inverse, identity), but when I check the assumptions (normality and homogeneity of residuals) these are not verified.

The general model setting is:

full_F <- glmer(Fundam_freq ~ Sex + Breed + Sex*Breed + 
             Context + (1 | Cat_ID), data = data, family = ?(link = "?"))

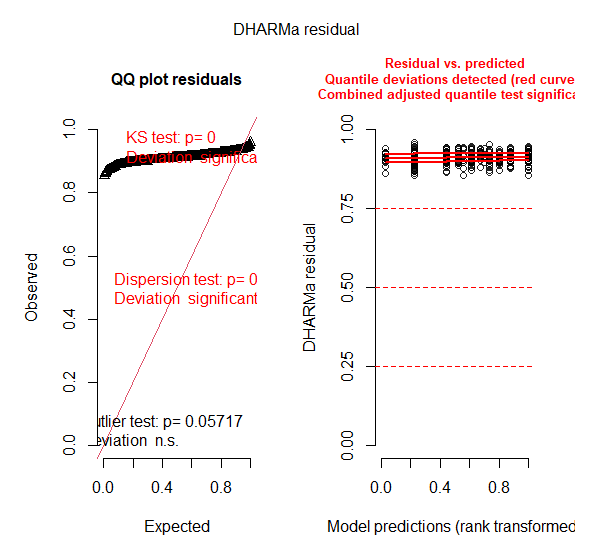
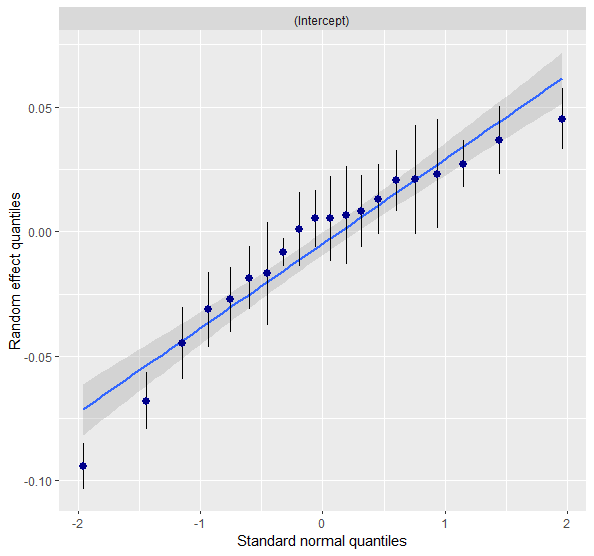
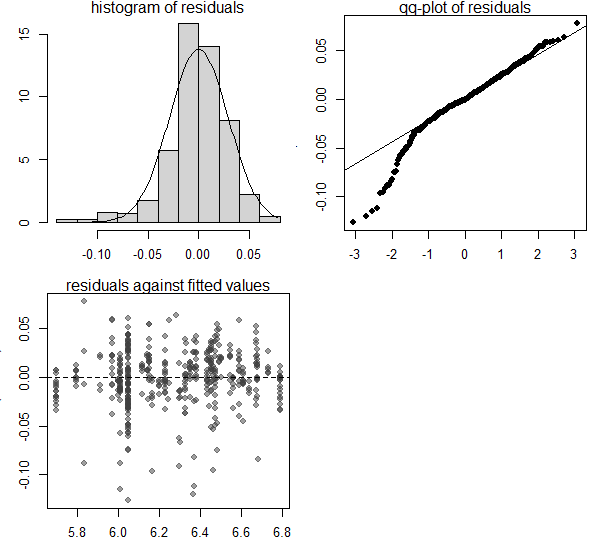
EXAMPLE WITH family=Gamma(link = "log") after having log-transformed + 1 the response variable. Here I attach images of checking residuals assumptions

1. Checking assumptions:

DHARMa::simulateResiduals(fittedModel = full_F, plot = T)

2. Checking assumptions with:

sjPlot::plot_model(full_F, type = "diag")

3. Checking assumptions with:

diagnostics.plot(full_F)

Which families and link functions do you recommend? Is there something I should do before run the glmm? (obviously, I transformed the Sex, Breed and Context into factors before run the model)

Thank you very much!

[mcneills]

You don't need Sex + Breed + SexBreed, as SexBreed includes the main effects of Sex and Breed, so Sex*Breed will do. Or alternatively, if you want to show main effects, use Sex + Breed + Sex:Breed, where the latter indicates an interaction.

Two humps? Not sure what to do there... You might need to break down the problem a little more.

When you say you do a logarithmic transformation with a gamma, I'm not sure if you mean that you fit the glmer() after doing the transformation. If so, that's not correct. You ought to do something like:

full_F <- glmer(Fundam_freq ~ Sex*Breed + Context + (1 | Cat_ID), data = data, family = Gamma(link = log))

Using the gamma family will use a log-transformation for the response, and you don't need to apply any transformation. Again, I'm not sure if that's what you actually did as it was not clear.

I don't use DHARMa::simulateResiduals() so I cannot help there.

The QQ plot of residuals suggests poor fitting at the bottom end of the range, which is unfortunately not uncommon. Having said that, you'd have to ask whether it's important to fit the upper or lower end of the range (or both). You might be able to get away with the model, but accept poor prediction of small values. Unfortunately, there are not many options in glmer() itself to help you, but you could try a transformation to improve fitting of small values, although I can't think offhand what would work best.

Stephen