Removing Outliers 3 SD away from mean of monoexponetial function in R

[zmcclean]

Hello,

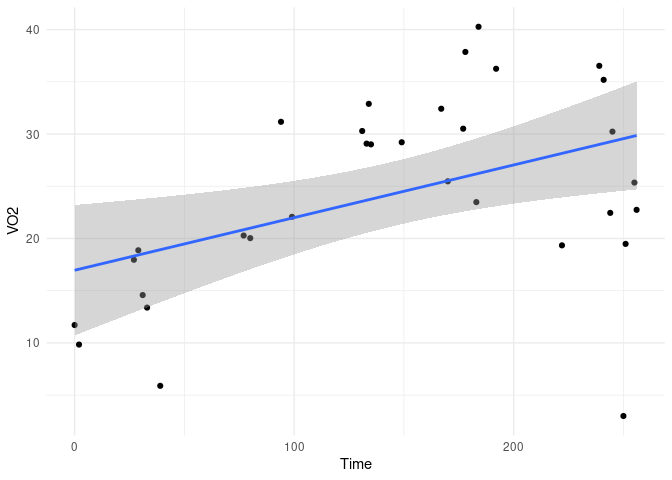
I have a large data set that analyzes exercising subjects' oxygen consumption over time (x= Time, y = VO2). This data fits a monoexponential function.

Here is a brief, sample data frame:

'''

 VO2 <- c(11.71,9.84,17.96,18.87,14.58,13.38,5.89,20.28,20.03,31.17,22.07,30.29,29.08,32.89,29.01,29.21,32.42,25.47,30.51,37.86,23.48,40.27,36.25,19.34,36.53,35.19,22.45,30.23,3,19.48,25.35,22.74)
 Time <- c(0,2,27,29,31,33,39,77,80,94,99,131,133,134,135,149,167,170,177,178,183,184,192,222,239,241,244,245,250,251,255,256)
 DF <- data.frame(VO2,Time)

'''

My primary question is the following:

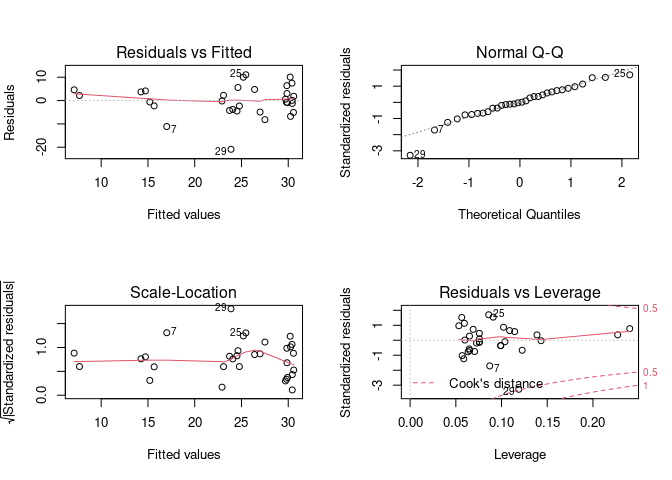
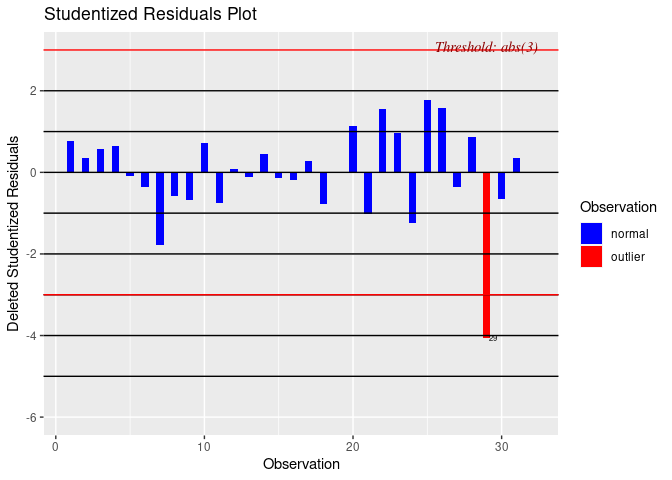
This data can be messy at points and needs to be cleaned. Using R, how do I remove outliers that occur +/- 3 standard deviations from the mean of a monoexponential function? Each data set I clean will be slightly different, so I would like R to fit some monoexponential function to the data and remove (replace with NA) all the outlying values. I then can continue manipulating the data to achieve my goal.

So far, I have this (unsuccessful) code to fit a function to the above data. Not only does it not fit well, but I am also unable to create a smooth function.

'''

 fit <- lm(VO2~poly(Time,2,raw=TRUE))
 xx <- seq(1,250, length=32)
 plot(Time,VO2,pch=19,ylim=c(0,50))+
 lines(xx, predict(fit, data.frame(DF=xx)), col="red")

'''

Thank you for the comments and valuable feedback. As I continue to learn and research, I will add to this post with successful/less successful attempts at the code for this process. Thank you for your knowledge, assistance and understanding.

[technocrat]

A reprex with only a handful of data would help, along with the code you are using for the single-variable exponential function (“monoexponental” seems to be a term mainly used in medical research). Add one line with an obvious outlier.

[zmcclean]

Thank you for your assistance so far on this. I have updated the question and hopefully have provided some additionally helpful details. Thank you for your time on this!

[startz]

Try

notOutlier <- abs(fit$residuals) < 3*(summary(fit)$sigma )

newVO2 <- VO2[notOutlier]
newTime <- Time[notOutlier]

Having said that, I don't understand why your fitted line doesn't look like a parabola. I'd be curious if someone could explain.

[technocrat]

Removing outliers is something of a dark art. It's hard to know where between reducing the data to only two points—to get a perfect fit—and removing obvious aberrant observations lies. This may get you started, using the three Studentized rule

library(ggplot2)
library(olsrr)
#> 
#> Attaching package: 'olsrr'
#> The following object is masked from 'package:datasets':
#> 
#>     rivers
DF <- data.frame(
  VO2 <- c(11.71, 9.84, 17.96, 18.87, 14.58, 13.38, 5.89, 20.28, 20.03, 31.17, 22.07, 30.29, 29.08, 32.89, 29.01, 29.21, 32.42, 25.47, 30.51, 37.86, 23.48, 40.27, 36.25, 19.34, 36.53, 35.19, 22.45, 30.23, 3, 19.48, 25.35, 22.74),
  Time <- c(0, 2, 27, 29, 31, 33, 39, 77, 80, 94, 99, 131, 133, 134, 135, 149, 167, 170, 177, 178, 183, 184, 192, 222, 239, 241, 244, 245, 250, 251, 255, 256)
)

fit <- lm(VO2~poly(Time,2,raw=TRUE))
summary(fit)
#> 
#> Call:
#> lm(formula = VO2 ~ poly(Time, 2, raw = TRUE))
#> 
#> Residuals:
#>      Min       1Q   Median       3Q      Max 
#> -20.8789  -3.9053  -0.0492   4.2572  11.0601 
#> 
#> Coefficients:
#>                              Estimate Std. Error t value Pr(>|t|)    
#> (Intercept)                 7.1052030  3.3286196   2.135 0.041375 *  
#> poly(Time, 2, raw = TRUE)1  0.2885680  0.0569580   5.066 2.11e-05 ***
#> poly(Time, 2, raw = TRUE)2 -0.0008859  0.0002049  -4.324 0.000165 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 6.791 on 29 degrees of freedom
#> Multiple R-squared:  0.5146, Adjusted R-squared:  0.4811 
#> F-statistic: 15.37 on 2 and 29 DF,  p-value: 2.81e-05

ggplot(DF,aes(Time,VO2)) + 
  geom_point() +
  geom_smooth(method = "lm") +
  theme_minimal()
#> `geom_smooth()` using formula 'y ~ x'

par(mfrow = c(2,2))
plot(fit)

ols_plot_resid_stud(fit) + theme_minimal()