Predictive capacities of Generalized Linear Models and significance

[Worg]

I have the following data

str(data)
'data.frame':   768 obs. of  5 variables:
 $ PIANTA     : chr  "C-1-R1-1" "C-1-R1-1" "C-1-R1-2" "C-1-R1-2" ...
 $ Trattamento: Factor w/ 4 levels "Controllo","Lidar",..: 1 1 1 1 1 1 1 1 1 1 ...
 $ Blocco     : Factor w/ 2 levels "1","2": 1 1 1 1 1 1 1 1 1 1 ...
 $ Replica    : chr  "R1" "R1" "R1" "R1" ...
 $ Risposta   : num  0 1 0 1 0 3 2 3 2 4 ...

I have a total of 768 observations. I would like to test whether the treatment (Trattamento) has a significant effect respect to my response variable (Risposta) and include the possible role of a blocking factor (Blocco). The response variable is numeric (ranging from 0 to 9) and assumes the value 0 for more than 400 observations.

Therefore I opted to use a negative binomial regression model using the following R code:

Call:
glm.nb(formula = Risposta ~ Trattamento + Blocco, data = data, 
    init.theta = 0.545484172, link = log)

Coefficients:
                    Estimate Std. Error z value Pr(>|z|)    
(Intercept)          0.26016    0.13268   1.961 0.049904 *  
TrattamentoLidar    -0.60387    0.17507  -3.449 0.000562 ***
TrattamentoRecupero -0.86591    0.18135  -4.775  1.8e-06 ***
TrattamentoStandard -0.35299    0.17027  -2.073 0.038159 *  
Blocco2             -0.03355    0.12671  -0.265 0.791162    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for Negative Binomial(0.5455) family taken to be 1)

    Null deviance: 677.61  on 767  degrees of freedom
Residual deviance: 651.46  on 763  degrees of freedom
AIC: 1916

Number of Fisher Scoring iterations: 1


              Theta:  0.5455 
          Std. Err.:  0.0654 

 2 x log-likelihood:  -1903.9550

I see that all treatments are significant with respect to the intercept (control) and that the block has no significant effect. I wanted to test the predictive capacities of the model and I have used the following code:

predicted <- predict(model1, type = "response")

predictions <- data.frame(Osservato = data$Risposta, Predetto = predicted)

plot(predictions$Osservato, predictions$Predetto, 
     xlab = "Observed", ylab = "Predicted",
     main = "")

abline(a = 0, b = 1, col = "red")

legend("topleft", legend = "Linea di riferimento", col = "red", lty = 1)

I obtain the following graph of predicted versus observed:

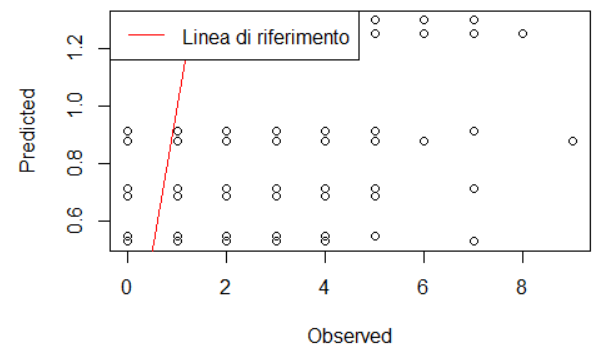
From the graph, it seems that the model is not good for predicting the values of my response variable. Given that, and considering that predicting values is not the scope of my study, can I still rely on the significance values obtained by the model?