Points of intersection of a curved line and a straight line

General
1

Hi I am currently tackling on how to find points of intersection on R studio, including a plot of the functions on the same plot. As you can see I have wrote out the constants and the simultaneous equation that needs to be solved to find theta, in order to find the value for 'k' and struggling on how to attempt this. Any help would be much appreciated!

#Constants given
L<-1.210^(-8)
u0<-1.610^(-19)23210^(-3)
m_star<-9.10910^(-31)
hbar<-(6.6310^(-34))/(2*pi)

me<-0.0679.10910^(-31)
mh<-0.59.10910^(-31)

#Equation for theta (unknown value is k)
theta<-(kL)/2
theta0<-sqrt(((m_star)(u0)(L^(2)))/(2(hbar^(2))))

#Simultaneous equations to solve
y<-theta
y<-theta0*cos(theta)

2

See the FAQ: How to do a minimal reproducible example reprex for beginners. Could you reframe the question along the following lines?

# constants
L <- 1.210^(-8)
u0 <- 1.610^(-19) * 23210^(-3)
m_star <- 9.10910^(-31)
hbar <- (6.6310^(-34)) / (2 * pi)
me <- 0.0679 * 10910^(-31)
mh <- 0.59 * 10910^(-31)
theta0 <- sqrt(((m_star) * (u0) * (L^(2))) / (2 * (hbar^(2))))

generate_theta <- function(k) (k*L)/2

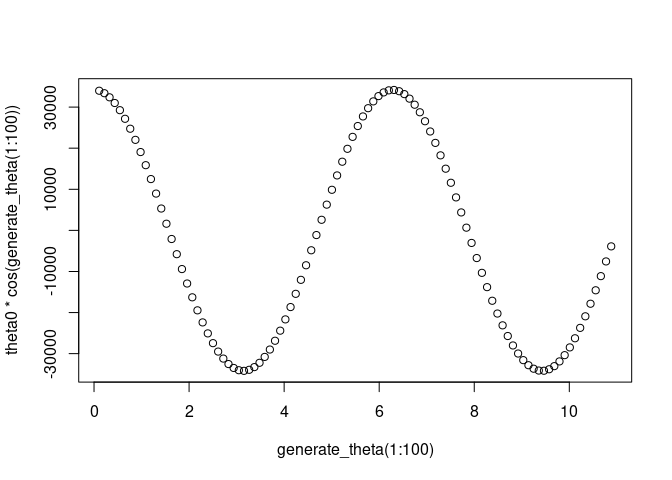
plot(generate_theta(1:100),theta0*cos(generate_theta(1:100)))

3

Hi, from generating the two functions I will need to find where y=theta and y=theta0*cos(theta)
to intersect on the plot and print the result

4

Also, some of the constants keep messing up when I post it here ill give you the list.

  1. there should be a '*' in between 1.2 and 10 for L, 1.6 and 10 for u0, 9.109 and 10 for m_star
  2. the equation for theta0, ''me'' should replace ''m_star''

the plot came out as below without changing any of the code you have wrote
Rplot

Similarly I need to almost create a graph like this
**

image
image872×488 34.6 KB
**

5

Cut, paste into your answer and edit this as required

L <- 1.210^(-8)
u0 <- 1.610^(-19) * 23210^(-3)
m_star <- 9.10910^(-31)
hbar <- (6.6310^(-34)) / (2 * pi)
me <- 0.0679 * 10910^(-31)
mh <- 0.59 * 10910^(-31)
theta0 <- sqrt(((m_star) * (u0) * (L^(2))) / (2 * (hbar^(2))))

Then m_star is not used?

You should recheck, cutting and pasting the code.

6

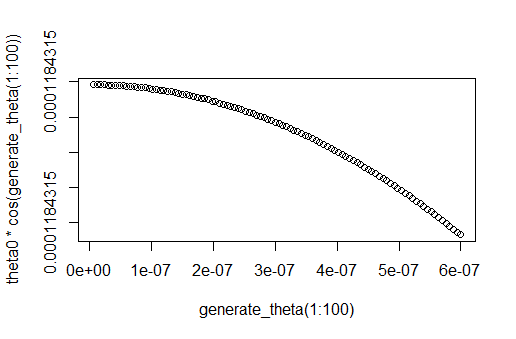
With the data, this will be difficult because the axes differ by 44 orders or magnitude

suppressPackageStartupMessages({
  library(ggplot2)
})

# constants
L <- 1.210^(-8)
u0 <- 1.610^(-19) * 23210^(-3)
m_star <- 9.10910^(-31)
hbar <- (6.6310^(-34)) / (2 * pi)
me <- 0.0679 * 10910^(-31)
mh <- 0.59 * 10910^(-31)
theta0 <- sqrt(((m_star) * (u0) * (L^(2))) / (2 * (hbar^(2))))

generate_theta <- function(k) (k*L)/2

runs <- seq(1,100)

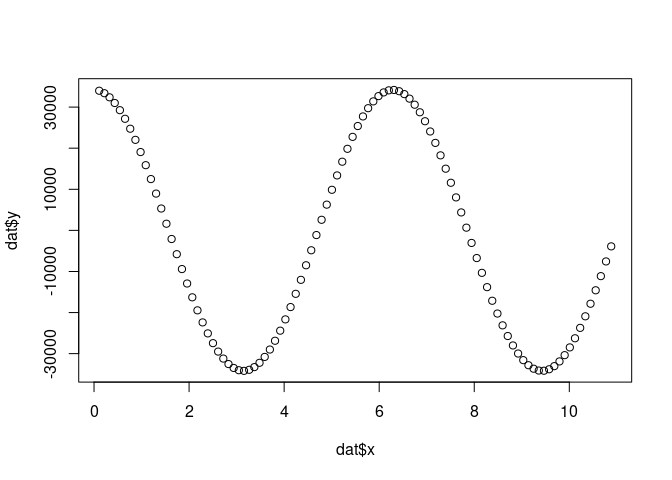
dat <- data.frame(x = generate_theta(runs),y = theta0*cos(generate_theta(runs)))

plot(dat$x,dat$y)


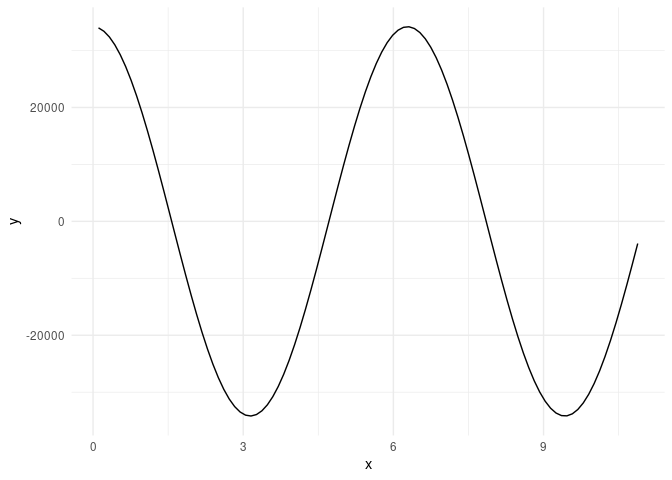
p <- ggplot(dat)
p + geom_line(aes(x,y)) +
    theme_minimal()


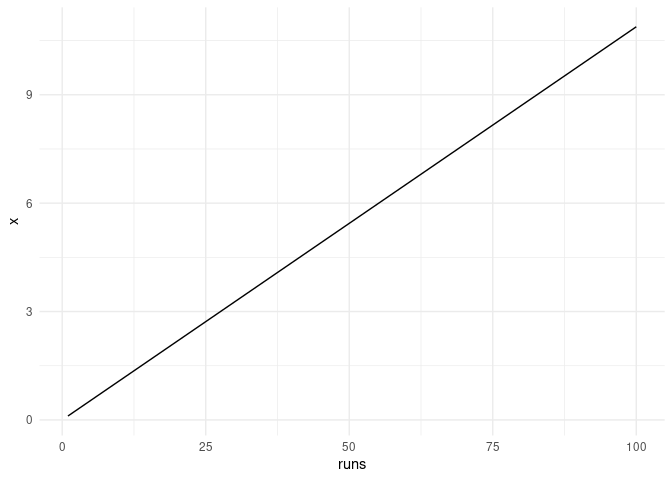
p + geom_line(aes(runs,x)) +
  theme_minimal()