I am working with the R programming language.
I tried to plot the Likelihood Function of a Normal Distribution:
library(plotly)
y <- rnorm(5,5,5)
my_function <- function(x1,x2) {
n = 20
a = n/2*log(2*pi)
b = n/2*log(x2^2)
c = 1/(2*x2^2)
d = sum ((y-x1)^2)
return (a + b + c* d)
}
input_1 <- seq(1, 10,0.1)
input_2 <- seq(1, 10,0.1)
z <- outer(input_1, input_2, my_function)
plot_ly(x = input_1, y = input_2, z = z) %>% add_surface()
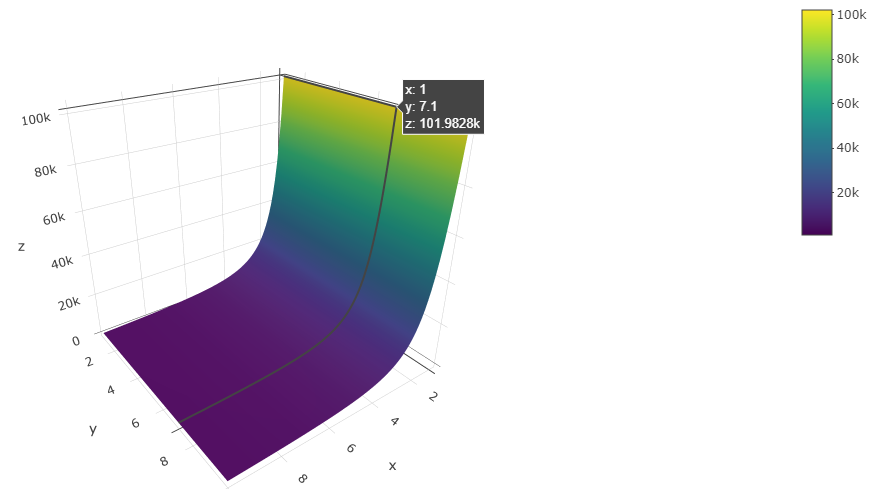
As we can see here, there some values on this graph that are close to 100,000:
However, over the range at which this function was evaluated, the function can never take such a large value. For example, if I were to evaluate this function at the same point that appears in the above picture, I get a value that is nowhere close to 100,000
my_function(1, 7.1)
[1] 59.94714
Have I plotted this function correctly? Why does the value in the picture not match with the value I get from manually evaluating the function? Can someone please explain why this is happening and what I can do to fix this problem?
Thanks!
Note:
- From a mathematics and statistics perspective, I don't think it is possible for the Likelihood Function of a Normal Distribution (for a small dataset generated from a Normal Distribution of mean = 5 and standard deviation = 5) could take such large values (Likelihood function - Wikipedia)
- I think the problem in this question is related to the
outer()function - I don't think the correct values of the function are being calculated via theouter()function (e.g. take for instance the discrepancy between 59.9 vs 120,000)