Play with least squares regression - Shiny Contest Submission

Conferences & Events Contests
1

Play with least squares regression

Authors: Tomas Capretto

Abstract: This application lets you explore how least squares fit works in simple linear regression. You can add points, fit the regression, and explore the contribution of each point to the squared error via an associated square in the plot.

Full Description:

Introduction

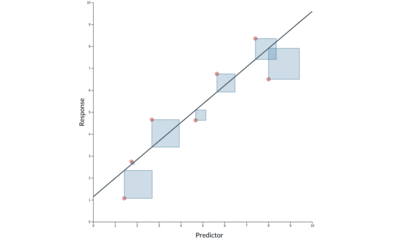
The objective of this application is to enable people to explore how least
squares fit works in simple linear regression. This method minimizes the sum
of the squared differences between each point and the estimation given by the
line. While it is hard to mentally visualize squared distances, it is quite
easy to compare squares. So this app lets you add points, fit linear
regressions, manipulate the parameters of the linear regression, and explore
the contribution of each point to the squared error via the associated square
in the plot.

Basic usage

The easiest way to start playing by clicking on the plot area. This will
add a point in the position of the cursor. A linear regression fit together
with a square that represents the contribution of the point to the sum of
squares.

  • Add random points adds 5 random points to the plot.
  • Shake points shakes all the existing points in the plot, mostly for fun.
  • Set Least Squares Fit lets you fit a regression line using Least Squares
    method. This can be used after manually tuning parameter estimates.
  • Parameter estimates represent the intercept and slope in the equation
    of the line. They are updated as points are modified but you can manipulate
    them manually.
  • Clear plot deletes all the points, squares, and line from the plot.

Finally, the sum of squares is shown below. Do you think you can
get a smaller error than least squares method?! Well, have a try and play!

Keywords: regression, least-squares, r2d3, shiny.semantic
Shiny app: https://tomicapretto.shinyapps.io/LeastSquaresRegression/
Repo: GitHub - tomicapretto/playwithregression: A Shiny application to play with simple linear regression fit via Least Squares method
RStudio Cloud: Posit Cloud

Thumbnail:
image

Full image: