NMDS point hidden behind another point

[dlrlanders]

Hi everyone,
I couldn't see a similar post on the forum so I haven't quoted another query/post here.

I am having some difficulty with an NMDS plot that I have created. I have six transects along with a rugosity reading and abundance data for each, as follows:

Transect	Rugosity	Acanthastrea_brevis	Acanthastrea_ishigakiensis	Acropora_digitifera	Acropora_divaricata	Acropora_gemmifera	Acropora_latistella
ARM018	0.606218508	0	0	0	100	0	100
ARM0115	0.615192661	25	100	50	0	0	0
ARM068	0.413580544	0	0	0	0	0	0
ARM0615	0.53388867	0	0	0	0	0	0
ARM078	0.700824123	0	0	0	0	100	0
ARM0715	0.768103537	75	0	50	0	0	0

Table 1. A sample of my data (you can see that ARM078 and ARM0715 have different data)


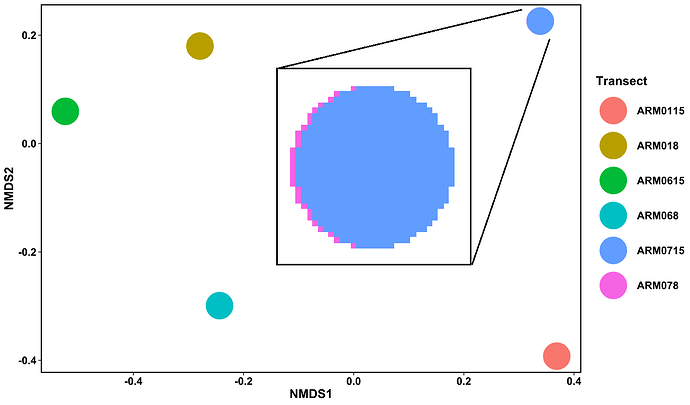
My issue is that I have 6 transects, but only 5 are showing on the NMDS plot. After some digging around to see I had generated the NMDS wrong I realised that a point could be hidden behind another so I altered the aesthetics of the plot to see if I could figure out where the missing point was. I noticed a faint pink line around the blue point:

Fig 1. My NMDS plot showing 5 points with a very zoomed in point ARM0715 (blue) showing a pink rim which could be hiding point ARM078

Non of the other points looks like this when zoomed in - they all have uniform colour. Changing the size and opacity of the points hasn't worked as the point is still hidden behind the other. Looking at Table 1 you can see that ARM078 and ARM0715 have different data so surely they shouldn't appear in exactly the same region?

My data has the shape 6 obs. of 51 variables.

Has anyone come across anything like this before? Or perhaps can think of a way for me to fix it? I though about maybe transposing the data and will try this next.

Any suggestions are very much appreciated. Thank you.

P.s. here is an outline of the nmds list object that I have generated in R:

Name	Type	Value
nmds	"list [36] (S3: metaMDS monoMDS)"	List of length 36
nobj	integer [1]	6
nfix	integer [1]	0
ndim	double [1]	2
ndis	integer [1]	15
ngrp	integer [1]	1
diss	double [15]	0.701 0.771 0.773 0.781 0.803 0.832 ...
iidx	integer [15]	6 4 4 3 5 5 ...
jidx	integer [15]	5 1 3 1 2 1 ...
xinit	double [12]	-0.229 0.336 -0.205 -0.491 0.298 0.292 ...
istart	integer [1]	1
isform	integer [1]	1
ities	integer [1]	1
iregn	integer [1]	1
iscal	integer [1]	1
maxits	integer [1]	200
sratmx	double [1]	0.999999
strmin	double [1]	1.00E-04
sfgrmn	double [1]	1.00E-07
dist	double [15]	0.000286 0.272546 0.454877 0.480353 0.619081 0.619261 ...
dhat	double [15]	0.000286 0.272546 0.454877 0.480353 0.619081 0.619221 ...
points	double [6 x 2]	-0.2790 0.3687 -0.2435 -0.5235 0.3385 0.3388 0.1799 -0.3923 -0.2991 0.0594 ...
stress	double [1]	7.60E-05
grstress	double [1]	7.60E-05
iters	integer [1]	11
icause	integer [1]	2
call	language	"metaMDS(comm = m_com, distance = ""bray"")"
model	character [1]	global
distmethod	character [1]	bray
distcall	character [1]	"'vegdist(x = comm, method = distance)'"
data	character [1]	wisconsin(sqrt(m_com))
distance	character [1]	bray
converged	double [1]	0
tries	double [1]	20
bestry	double [1]	0
engine	character [1]	monoMDS
species	double [49 x 2]	0.408 0.428 0.413 -0.324 0.393 -0.324 -0.049 -0.492 -0.155 0.226 0.283 0. ...

[technocrat]

A reprex (see the FAQ) will attract more answers because it won't be necessary to reverse engineer a data set and plot command that reproduces the problem. Without that you depend on the luck of the draw in someone seeing this who has run across the identical problem.

[dlrlanders]

Apologies - thank you for the advice.

In a roundabout way, I was simply asking for a reason(s) why would two points on an NMDS plot might appear on top on one another and how to fix this.

For anyone who is curious or for future reference, I just tried asking ChatGPT which has suggested the following:

"If two points appear on top of each other in an NMDS plot, it suggests that the dissimilarity (or similarity) values between those points are effectively the same. This could occur for a few reasons:

1. Data Integrity: If the data was not processed correctly or there are errors in the dataset, it could lead to artificially identical dissimilarity values between certain points.
2. Metric Properties: The choice of dissimilarity or similarity metric can impact how points are positioned in the NMDS plot. If a specific metric is used that tends to make points with similar characteristics collapse onto each other, this could lead to overlapping points.
3. High Dimensionality: NMDS reduces the dimensionality of the data while preserving pairwise dissimilarity or similarity relationships as closely as possible. However, in high-dimensional spaces, it becomes more challenging to accurately represent the relationships, potentially causing points to overlap.
4. Data Structure: If the data has a specific structure where certain groups of points are very similar to each other and dissimilar to points outside the group, it might lead to these points collapsing onto each other in the NMDS plot.
5. Noise and Variability: No dataset is entirely free from noise or variability. Even a small amount of noise can influence the dissimilarity calculations and lead to points clustering together in the NMDS plot.

To address this issue, you might want to consider the following steps:

• If possible, investigate the original data and the relationships between those points to gain a deeper understanding of why they are so similar.
• Consider whether it makes sense for those points to be so similar and whether any specific data preprocessing or transformation is needed.
• Double-check the dissimilarity calculations for accuracy.
• Try using different dissimilarity or similarity metrics to see if they yield different results."

I am just going back to see whether I can perform the individual dissimilarity calculations using the two points to find out their true measure of dissimilarity.