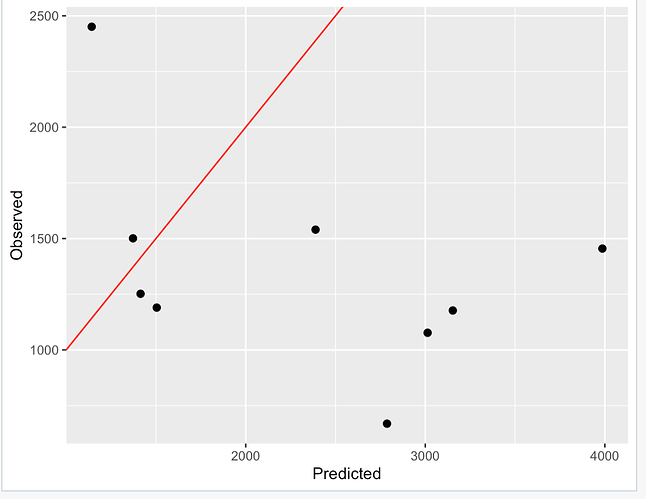
As @FJCC commented, you can use MSE/RMSE to evaluate the performance of your model. In your case, it seems that you are looking for a significant test at some levels, say 95%. In that case, you can use "confint" function to achieve that.
To answer your queries, try to follow the codes below;
df <- mtcars
df['price'] <- sample(400 : 2500, size = nrow(df)) # Add a column of price just as you did.
# Splitting data for train and test
ind <- sample(nrow(df), size = 0.7*nrow(df), replace = F) # We use 70% of the df in Training
df_Train <- df[ind, ]
df_Test <- df[-ind, ]
# Train/Develop the model. We use all predictors in df, with price as predictand/response
fit_model <- lm(price ~., data = df_Train) # Build the model
# Note that, not all variables can influence your response.
summary(fit_model) # See the summary.
#>
#> Call:
#> lm(formula = price ~ ., data = df_Train)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -893.6 -310.7 -106.2 463.0 929.8
#>
#> Coefficients: (1 not defined because of singularities)
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 20369.9266 18509.6209 1.101 0.295
#> mpg 43.1637 80.5942 0.536 0.603
#> cyl -13.6964 466.4630 -0.029 0.977
#> disp 0.4528 5.4551 0.083 0.935
#> hp -22.1046 15.1269 -1.461 0.172
#> drat -784.2134 767.5272 -1.022 0.329
#> wt 1032.8341 927.6895 1.113 0.289
#> qsec -983.6680 783.9803 -1.255 0.236
#> vs 2195.7889 1226.8170 1.790 0.101
#> am NA NA NA NA
#> gear -401.9742 1042.7835 -0.385 0.707
#> carb 179.6202 378.8715 0.474 0.645
#>
#> Residual standard error: 694.4 on 11 degrees of freedom
#> Multiple R-squared: 0.3338, Adjusted R-squared: -0.2719
#> F-statistic: 0.5511 on 10 and 11 DF, p-value: 0.8214
# You need predictors with at least one (1) star after column Pr(>|t|) from summary.
# In this case it seems all our predictors are insignificant, since no any star at the end from summary.
# Alternatively you can use the package "relaimpo" to calculate/identify the importances of your predictors
# Also you can see other informations from your fit model.
fit_model$coefficients
#> (Intercept) mpg cyl disp hp
#> 20369.9266334 43.1636595 -13.6964068 0.4527914 -22.1045852
#> drat wt qsec vs am
#> -784.2134301 1032.8341046 -983.6680210 2195.7889354 NA
#> gear carb
#> -401.9741836 179.6202151
fit_model$effects ; # etc Use fit_model$xxxxx to see other information
#> (Intercept) mpg cyl disp hp drat
#> -5994.77774 10.74388 407.84285 -50.38455 402.13553 280.52474
#> wt qsec vs gear carb
#> -570.41721 -168.51445 -1335.25978 56.75030 -329.23028 -699.83919
#>
#> 475.19803 556.15428 201.00593 -210.30365 759.28810 1303.91192
#>
#> -763.31647 110.00162 545.77770 1012.86774
# Also you can check the the confidence interval from your model
confint(fit_model)
#> 2.5 % 97.5 %
#> (Intercept) -20369.47434 61109.32760
#> mpg -134.22302 220.55034
#> cyl -1040.37465 1012.98183
#> disp -11.55385 12.45943
#> hp -55.39875 11.18958
#> drat -2473.52946 905.10259
#> wt -1008.99661 3074.66482
#> qsec -2709.19708 741.86104
#> vs -504.41701 4895.99488
#> am NA NA
#> gear -2697.12529 1893.17692
#> carb -654.27023 1013.51066
confint(fit_model, level = .95)
#> 2.5 % 97.5 %
#> (Intercept) -20369.47434 61109.32760
#> mpg -134.22302 220.55034
#> cyl -1040.37465 1012.98183
#> disp -11.55385 12.45943
#> hp -55.39875 11.18958
#> drat -2473.52946 905.10259
#> wt -1008.99661 3074.66482
#> qsec -2709.19708 741.86104
#> vs -504.41701 4895.99488
#> am NA NA
#> gear -2697.12529 1893.17692
#> carb -654.27023 1013.51066
# Type help(confint) of ??confint for help
# Test the model/Predicting
# You can use predict() from base-R package called "stats" which loads by deafult
pred_model <- predict(fit_model, newdata = df_Test) #
#> Warning in predict.lm(fit_model, newdata = df_Test): prediction from a rank-
#> deficient fit may be misleading
# Get the data for further analysis
df_anly <- data.frame(df_Test['price'], 'pred' = pred_model)
df_anly['Names'] <- rownames(df_anly)
reshape2::melt(df_anly, id = 'Names') |>
ggplot2::ggplot( aes( x = Names, y = value, group = variable, color = variable) ) +
geom_line(size = 1) + geom_point(size = 2)
# Let us assess the performance of our developed model using RMSE
rmse1 <- sqrt(mean((df_anly$pred - df_anly$price)**2))
print(rmse1)
#> [1] 1751.047
# Here I use the 'measures' package to calculate the RMSE
rmse2 <- measures::RMSE(truth = df_anly$price, response = df_anly$pred)
print(rmse2)
#> [1] 1751.047
Alternatively, you can use matrix multiplications for multiple predictors. Just see my response at nls fit function with summation - #2 by pe2ju. Here I post the workaround;
Suppose your data is in Matrix form and use Matrix Multiplications to perform the linear regressions. Suppose a data frame of 2 predictors/regressors and the parameters 'a' as a constant and coefficients B [b1 and b2] since we have 2 regressors. Then, you go smoothly as follows;
predic <- data.frame( 'Model_01' = rnorm(50, mean = 4.5, sd = 1.5 ),
'Model_02' = rnorm(50, mean = 3.5, sd = 1.2 ) )
predic2Mat <- as.matrix(predic, byrow = F)
predic2Mat <- cbind(rep(1, nrow(predic2Mat)), predic2Mat) # We add 1 for mutrix multiplications
pars <- c('a' = 2, 'b1' = 3.5, 'b2' = 1.8) # a = constant, b1 & b2 are coefficients from your model
new_pred <- predic2Mat %*% pars # Get the new predictions
For further useful elaborations on Linear Regression. Just follow these links;
https://rpubs.com/aaronsc32/regression-confidence-prediction-intervals#:~:text=To%20find%20the%20confidence%20interval,to%20output%20the%20mean%20interval