Hi all,
I would like to ask for your help in identifying the R square value (i.e., coefficient of determination) in this result. I am trying to compare the hypothesis model and competing model with the R square value, but I couldn't figure out where it is.
Thanks!
Sys.setenv(LANG = "En")
library(lavaan)
#> This is lavaan 0.6-7
#> lavaan is BETA software! Please report any bugs.
library(semPlot)
#> Registered S3 methods overwritten by 'huge':
#> method from
#> plot.sim BDgraph
#> print.sim BDgraph
#built in data
data(PoliticalDemocracy)
model <- '
# measurement model
ind60 =~ x1 + x2 + x3
dem60 =~ y1 + y2 + y3 + y4
dem65 =~ y5 + y6 + y7 + y8
# regressions
dem60 ~ ind60
dem65 ~ ind60 + dem60
# residual correlations
y1 ~~ y5
y2 ~~ y4 + y6
y3 ~~ y7
y4 ~~ y8
y6 ~~ y8
'
fit <- sem(model, data=PoliticalDemocracy)
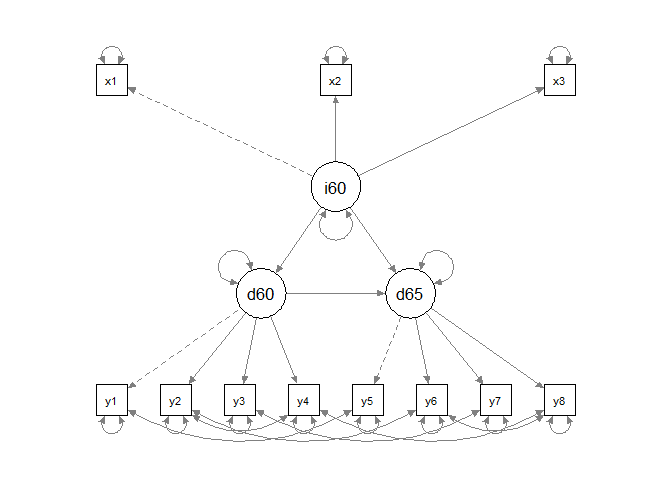
semPaths(fit)
summary(fit, standardized=TRUE, fit.measures=T)
#> lavaan 0.6-7 ended normally after 68 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of free parameters 31
#>
#> Number of observations 75
#>
#> Model Test User Model:
#>
#> Test statistic 38.125
#> Degrees of freedom 35
#> P-value (Chi-square) 0.329
#>
#> Model Test Baseline Model:
#>
#> Test statistic 730.654
#> Degrees of freedom 55
#> P-value 0.000
#>
#> User Model versus Baseline Model:
#>
#> Comparative Fit Index (CFI) 0.995
#> Tucker-Lewis Index (TLI) 0.993
#>
#> Loglikelihood and Information Criteria:
#>
#> Loglikelihood user model (H0) -1547.791
#> Loglikelihood unrestricted model (H1) -1528.728
#>
#> Akaike (AIC) 3157.582
#> Bayesian (BIC) 3229.424
#> Sample-size adjusted Bayesian (BIC) 3131.720
#>
#> Root Mean Square Error of Approximation:
#>
#> RMSEA 0.035
#> 90 Percent confidence interval - lower 0.000
#> 90 Percent confidence interval - upper 0.092
#> P-value RMSEA <= 0.05 0.611
#>
#> Standardized Root Mean Square Residual:
#>
#> SRMR 0.044
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Expected
#> Information saturated (h1) model Structured
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> ind60 =~
#> x1 1.000 0.670 0.920
#> x2 2.180 0.139 15.742 0.000 1.460 0.973
#> x3 1.819 0.152 11.967 0.000 1.218 0.872
#> dem60 =~
#> y1 1.000 2.223 0.850
#> y2 1.257 0.182 6.889 0.000 2.794 0.717
#> y3 1.058 0.151 6.987 0.000 2.351 0.722
#> y4 1.265 0.145 8.722 0.000 2.812 0.846
#> dem65 =~
#> y5 1.000 2.103 0.808
#> y6 1.186 0.169 7.024 0.000 2.493 0.746
#> y7 1.280 0.160 8.002 0.000 2.691 0.824
#> y8 1.266 0.158 8.007 0.000 2.662 0.828
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> dem60 ~
#> ind60 1.483 0.399 3.715 0.000 0.447 0.447
#> dem65 ~
#> ind60 0.572 0.221 2.586 0.010 0.182 0.182
#> dem60 0.837 0.098 8.514 0.000 0.885 0.885
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> .y1 ~~
#> .y5 0.624 0.358 1.741 0.082 0.624 0.296
#> .y2 ~~
#> .y4 1.313 0.702 1.871 0.061 1.313 0.273
#> .y6 2.153 0.734 2.934 0.003 2.153 0.356
#> .y3 ~~
#> .y7 0.795 0.608 1.308 0.191 0.795 0.191
#> .y4 ~~
#> .y8 0.348 0.442 0.787 0.431 0.348 0.109
#> .y6 ~~
#> .y8 1.356 0.568 2.386 0.017 1.356 0.338
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> .x1 0.082 0.019 4.184 0.000 0.082 0.154
#> .x2 0.120 0.070 1.718 0.086 0.120 0.053
#> .x3 0.467 0.090 5.177 0.000 0.467 0.239
#> .y1 1.891 0.444 4.256 0.000 1.891 0.277
#> .y2 7.373 1.374 5.366 0.000 7.373 0.486
#> .y3 5.067 0.952 5.324 0.000 5.067 0.478
#> .y4 3.148 0.739 4.261 0.000 3.148 0.285
#> .y5 2.351 0.480 4.895 0.000 2.351 0.347
#> .y6 4.954 0.914 5.419 0.000 4.954 0.443
#> .y7 3.431 0.713 4.814 0.000 3.431 0.322
#> .y8 3.254 0.695 4.685 0.000 3.254 0.315
#> ind60 0.448 0.087 5.173 0.000 1.000 1.000
#> .dem60 3.956 0.921 4.295 0.000 0.800 0.800
#> .dem65 0.172 0.215 0.803 0.422 0.039 0.039
Created on 2021-02-04 by the reprex package (v0.3.0)