Hey,
looking at the lavaan::sem output, is z-value the beta-coefficient? If not, how do I get to it?
Defined Parameters:
Estimate Std.Err z-value P(>|z|)
a1b -0.019 0.011 -1.703 0.088
a2b -0.034 0.017 -1.957 0.050
totalSOP 0.125 0.056 2.223 0.026
totalSPP -0.114 0.056 -2.024 0.043
indexModMedSPP -0.027 0.016 -1.646 0.100
indexModMedSOP 0.005 0.007 0.608 0.543
It is really difficult to read it like that and especially without being able to see the network. Able to post a reprex? FAQ: How to do a minimal reproducible example ( reprex ) for beginners
Hi,
actually I only need to know about the first line.
Estimate Std.Err z-value P(>|z|)
The results are secondary. I just need to know which line to report.
Your estimate should be your beta-coefficient. Z-value is not your beta-coefficient - this is the critical value telling you if this is a significant contributor to your DV as an IV. See the example below as printed from Lavaan:
## Latent Variables:
## Estimate Std.Err z-value P(>|z|)
## visual =~
## x1 1.000
## x2 0.554 0.100 5.554 0.000
## x3 0.729 0.109 6.685 0.000
## textual =~
## x4 1.000
## x5 1.113 0.065 17.014 0.000
## x6 0.926 0.055 16.703 0.000
## speed =~
## x7 1.000
## x8 1.180 0.165 7.152 0.000
## x9 1.082 0.151 7.155 0.000
OK, so just to avoid any further missunderstanding.
My estimate value is not the b value but the standardized beta coefficient?!
I calculated a path analysis with lavaan.
No, that is your beta coefficients...not standardised. It honestly helps if you do a proper reprex...Below you can see how to get standardised beta coefficients with standardizedSolution
library(lavaan)
#> This is lavaan 0.6-7
#> lavaan is BETA software! Please report any bugs.
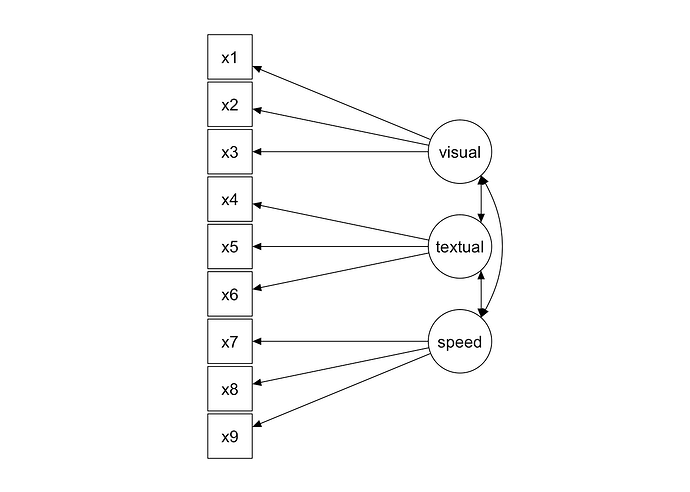
HS.model <- " visual =~ x1 + x2 + x3
textual =~ x4 + x5 + x6
speed =~ x7 + x8 + x9 "
fit <- cfa(HS.model, data = HolzingerSwineford1939)
standardizedSolution(fit, type = "std.all")
#> lhs op rhs est.std se z pvalue ci.lower ci.upper
#> 1 visual =~ x1 0.772 0.055 14.041 0 0.664 0.880
#> 2 visual =~ x2 0.424 0.060 7.105 0 0.307 0.540
#> 3 visual =~ x3 0.581 0.055 10.539 0 0.473 0.689
#> 4 textual =~ x4 0.852 0.023 37.776 0 0.807 0.896
#> 5 textual =~ x5 0.855 0.022 38.273 0 0.811 0.899
#> 6 textual =~ x6 0.838 0.023 35.881 0 0.792 0.884
#> 7 speed =~ x7 0.570 0.053 10.714 0 0.465 0.674
#> 8 speed =~ x8 0.723 0.051 14.309 0 0.624 0.822
#> 9 speed =~ x9 0.665 0.051 13.015 0 0.565 0.765
#> 10 x1 ~~ x1 0.404 0.085 4.763 0 0.238 0.571
#> 11 x2 ~~ x2 0.821 0.051 16.246 0 0.722 0.920
#> 12 x3 ~~ x3 0.662 0.064 10.334 0 0.537 0.788
#> 13 x4 ~~ x4 0.275 0.038 7.157 0 0.200 0.350
#> 14 x5 ~~ x5 0.269 0.038 7.037 0 0.194 0.344
#> 15 x6 ~~ x6 0.298 0.039 7.606 0 0.221 0.374
#> 16 x7 ~~ x7 0.676 0.061 11.160 0 0.557 0.794
#> 17 x8 ~~ x8 0.477 0.073 6.531 0 0.334 0.620
#> 18 x9 ~~ x9 0.558 0.068 8.208 0 0.425 0.691
#> 19 visual ~~ visual 1.000 0.000 NA NA 1.000 1.000
#> 20 textual ~~ textual 1.000 0.000 NA NA 1.000 1.000
#> 21 speed ~~ speed 1.000 0.000 NA NA 1.000 1.000
#> 22 visual ~~ textual 0.459 0.064 7.189 0 0.334 0.584
#> 23 visual ~~ speed 0.471 0.073 6.461 0 0.328 0.613
#> 24 textual ~~ speed 0.283 0.069 4.117 0 0.148 0.418
Created on 2020-10-14 by the reprex package (v0.3.0)
Have a read here too: https://psu-psychology.github.io/r-bootcamp-2018/talks/lavaan_tutorial.html#standardized-estimates
Ahh, I think I got it.
standardizedsolution() gives the same results as in parameterestimates(model, standardized=T), looking at std.all, right?
Is it possible that we also have a misunderstanding due to translation problems?
Namely, that my b is your beta and my beta your standardized beta coefficient?
See. This is exactly why it helps if you share code because then we can actually check it
library(lavaan)
#> This is lavaan 0.6-7
#> lavaan is BETA software! Please report any bugs.
HS.model <- " visual =~ x1 + x2 + x3
textual =~ x4 + x5 + x6
speed =~ x7 + x8 + x9 "
fit <- cfa(HS.model, data = HolzingerSwineford1939)
standardizedSolution(fit, type = "std.all")
#> lhs op rhs est.std se z pvalue ci.lower ci.upper
#> 1 visual =~ x1 0.772 0.055 14.041 0 0.664 0.880
#> 2 visual =~ x2 0.424 0.060 7.105 0 0.307 0.540
#> 3 visual =~ x3 0.581 0.055 10.539 0 0.473 0.689
#> 4 textual =~ x4 0.852 0.023 37.776 0 0.807 0.896
#> 5 textual =~ x5 0.855 0.022 38.273 0 0.811 0.899
#> 6 textual =~ x6 0.838 0.023 35.881 0 0.792 0.884
#> 7 speed =~ x7 0.570 0.053 10.714 0 0.465 0.674
#> 8 speed =~ x8 0.723 0.051 14.309 0 0.624 0.822
#> 9 speed =~ x9 0.665 0.051 13.015 0 0.565 0.765
#> 10 x1 ~~ x1 0.404 0.085 4.763 0 0.238 0.571
#> 11 x2 ~~ x2 0.821 0.051 16.246 0 0.722 0.920
#> 12 x3 ~~ x3 0.662 0.064 10.334 0 0.537 0.788
#> 13 x4 ~~ x4 0.275 0.038 7.157 0 0.200 0.350
#> 14 x5 ~~ x5 0.269 0.038 7.037 0 0.194 0.344
#> 15 x6 ~~ x6 0.298 0.039 7.606 0 0.221 0.374
#> 16 x7 ~~ x7 0.676 0.061 11.160 0 0.557 0.794
#> 17 x8 ~~ x8 0.477 0.073 6.531 0 0.334 0.620
#> 18 x9 ~~ x9 0.558 0.068 8.208 0 0.425 0.691
#> 19 visual ~~ visual 1.000 0.000 NA NA 1.000 1.000
#> 20 textual ~~ textual 1.000 0.000 NA NA 1.000 1.000
#> 21 speed ~~ speed 1.000 0.000 NA NA 1.000 1.000
#> 22 visual ~~ textual 0.459 0.064 7.189 0 0.334 0.584
#> 23 visual ~~ speed 0.471 0.073 6.461 0 0.328 0.613
#> 24 textual ~~ speed 0.283 0.069 4.117 0 0.148 0.418
HS.model <- ' visual =~ x1 + x2 + x3
textual =~ x4 + x5 + x6
speed =~ x7 + x8 + x9 '
fit <- cfa(HS.model, data=HolzingerSwineford1939)
parameterEstimates(fit, standardized=TRUE)
#> lhs op rhs est se z pvalue ci.lower ci.upper std.lv
#> 1 visual =~ x1 1.000 0.000 NA NA 1.000 1.000 0.900
#> 2 visual =~ x2 0.554 0.100 5.554 0 0.358 0.749 0.498
#> 3 visual =~ x3 0.729 0.109 6.685 0 0.516 0.943 0.656
#> 4 textual =~ x4 1.000 0.000 NA NA 1.000 1.000 0.990
#> 5 textual =~ x5 1.113 0.065 17.014 0 0.985 1.241 1.102
#> 6 textual =~ x6 0.926 0.055 16.703 0 0.817 1.035 0.917
#> 7 speed =~ x7 1.000 0.000 NA NA 1.000 1.000 0.619
#> 8 speed =~ x8 1.180 0.165 7.152 0 0.857 1.503 0.731
#> 9 speed =~ x9 1.082 0.151 7.155 0 0.785 1.378 0.670
#> 10 x1 ~~ x1 0.549 0.114 4.833 0 0.326 0.772 0.549
#> 11 x2 ~~ x2 1.134 0.102 11.146 0 0.934 1.333 1.134
#> 12 x3 ~~ x3 0.844 0.091 9.317 0 0.667 1.022 0.844
#> 13 x4 ~~ x4 0.371 0.048 7.779 0 0.278 0.465 0.371
#> 14 x5 ~~ x5 0.446 0.058 7.642 0 0.332 0.561 0.446
#> 15 x6 ~~ x6 0.356 0.043 8.277 0 0.272 0.441 0.356
#> 16 x7 ~~ x7 0.799 0.081 9.823 0 0.640 0.959 0.799
#> 17 x8 ~~ x8 0.488 0.074 6.573 0 0.342 0.633 0.488
#> 18 x9 ~~ x9 0.566 0.071 8.003 0 0.427 0.705 0.566
#> 19 visual ~~ visual 0.809 0.145 5.564 0 0.524 1.094 1.000
#> 20 textual ~~ textual 0.979 0.112 8.737 0 0.760 1.199 1.000
#> 21 speed ~~ speed 0.384 0.086 4.451 0 0.215 0.553 1.000
#> 22 visual ~~ textual 0.408 0.074 5.552 0 0.264 0.552 0.459
#> 23 visual ~~ speed 0.262 0.056 4.660 0 0.152 0.373 0.471
#> 24 textual ~~ speed 0.173 0.049 3.518 0 0.077 0.270 0.283
#> std.all std.nox
#> 1 0.772 0.772
#> 2 0.424 0.424
#> 3 0.581 0.581
#> 4 0.852 0.852
#> 5 0.855 0.855
#> 6 0.838 0.838
#> 7 0.570 0.570
#> 8 0.723 0.723
#> 9 0.665 0.665
#> 10 0.404 0.404
#> 11 0.821 0.821
#> 12 0.662 0.662
#> 13 0.275 0.275
#> 14 0.269 0.269
#> 15 0.298 0.298
#> 16 0.676 0.676
#> 17 0.477 0.477
#> 18 0.558 0.558
#> 19 1.000 1.000
#> 20 1.000 1.000
#> 21 1.000 1.000
#> 22 0.459 0.459
#> 23 0.471 0.471
#> 24 0.283 0.283
Created on 2020-10-14 by the reprex package (v0.3.0)
Look at the function as well it clearly says:
Logical. If TRUE, standardized estimates are added to the output. Note that SEs and tests are still based on unstandardized estimates. Use standardizedSolution to obtain SEs and test statistics for standardized estimates
So it looks as if std.all is the same in yours as what est.std is on the one I run. Once again - note the warning above ^
Give me a minuite I am already working on the reprex. 
datapasta::df_paste(head(data_JS2, 5))
#> Error in head(data_JS2, 5): Objekt 'data_JS2' nicht gefunden
data.frame(
JSz.MA = c(-0.140374517602763,
0.624666603332296,-1.67045675947288,1.38970772426735,-0.140374517602763),
SOPz.MA = c(0.914927426378375,
-0.260637479027238,1.11085491061264,0.718999942144106,0.523072457909837),
SPPz.MA = c(-0.773403836221116,
-0.923316731564509,-1.0732296269079,-0.0238393595041482,
0.275986431182639),
TPz.MA = c(-1.10152234808083,
0.664153180460502,0.958432435217391,-1.69008085759461,1.25271168997428),
SOPz.MAxTPz.MA = c(-1.00781300702786,
-0.173103210643148,1.06467937715167,-1.21516803882939,0.655258982727233),
SPPz.MAxTPz.MA = c(0.851921609689008,
-0.613223743840965,-1.02861808486479,0.040290445155277,0.345731428616774)
)
#> JSz.MA SOPz.MA SPPz.MA TPz.MA SOPz.MAxTPz.MA SPPz.MAxTPz.MA
#> 1 -0.1403745 0.9149274 -0.77340384 -1.1015223 -1.0078130 0.85192161
#> 2 0.6246666 -0.2606375 -0.92331673 0.6641532 -0.1731032 -0.61322374
#> 3 -1.6704568 1.1108549 -1.07322963 0.9584324 1.0646794 -1.02861808
#> 4 1.3897077 0.7189999 -0.02383936 -1.6900809 -1.2151680 0.04029045
#> 5 -0.1403745 0.5230725 0.27598643 1.2527117 0.6552590 0.34573143
Created on 2020-10-15 by the reprex package (v0.3.0)
Thank you!!!
The advantage of the standardizedsolution() are the standardized SEs, which I dont have using parameterestmimates().
PS, you didnt mean the reprex anymore but code, right? Sorry its getting late over here...
Most welcome 
Feel free to mark my previous post with code as the solution.
The default should always be standardizedsolution given most use cases and being able to fairly interpret the rest of your output based on that standardisation.
Reprex is as much data as it is code A reproduceable example just makes it easy to quickly talk about the same thing and output without any other assumptions. I made use of the example above as it is data saved in lavaan. So if you don't necessarily want to share data you can setup your problem via a "dummy" data set like I did above to make it easy to at least demonstrate where and what is different and then just translate it back to your original problem with your actual data.
OK, one more question before I can go to sleep...
Due to a high probability of multucollinearity I z-standardized my variables before I calculated my model estimates. Aren't my estimates automatically standardized beta coefficients because of that?
This topic was automatically closed 7 days after the last reply. New replies are no longer allowed.
If you have a query related to it or one of the replies, start a new topic and refer back with a link.