Kolmogorov–Smirnov normality test

[Amiira]

I have a sample size of 6362620, is it reliable to use Kolmogorov–Smirnov normality test on such large sample size and why? Can I have a reference paper for it too if possible. Thanks

[nirgrahamuk]

(https://www.bristol.ac.uk/cmm/media/research/ba-teaching-ebooks/pdf/Normality%20-%20Practical.pdf)

in short

1. larger samples are more sensitive to rejecting the null hypothesis; so the statistician must use their knowledge and skill to interpret the statistic

Significance will be strongly affected by the number of
observations and so only a small discrepancy from normality will be deemed significant for very large sample sizes as may be the case here
whilst very large discrepancies will be required to reject the null hypothesis for small sample sizes

2. often when we have large samples, the analysis we might want to do, dont rely heavily on normality requirements

It should also be remembered that many
parametric statistics are robust to non-normality when sample sizes are very large (employing the Central Limit Theorem), so the
implications of non-normality are primarily of interest is designs with smaller sample sizes

[jrkrideau]

As a non-statistician, I would interpret nirgrahamuk's answer to mean that unless you have strong reasons to suspect non-normality it is unlikely to be as issue. With an N that size anything is likely to be "significant" .

I would suggest plotting the data first. The Anscombe's quartet is a good object lesson.

[Amiira]

Thank you so much. It is very informative!

[Amiira]

Hello @nirgrahamuk, I was researching, but could not really find the name of the author who this:

Normality%20-%20Practical.pdf

Grateful if you could direct me to it. Thanks!

[Andrzej]

There is down below a link to good deliberations about that subject:
https://stats.stackexchange.com/questions/2492/is-normality-testing-essentially-useless

and here:
https://my.linkedin.com/posts/adrianolszewski_clinicaltrials-statistics-datascience-activity-6996402323140849664-7zgy?trk=public_profile_like_view

regards,

[Amiira]

Thank you very much @Andrzej

[Andrzej]

You are welcome,
There are up there in my first link some entended materials about what nirgrahamuk and jrkrideau explained in their posts.
Additionally you can have a look at this link by Prof. A. Field:
https://www.discoveringstatistics.com/repository/exploringdata.pdf

On page 6 and later you will find about normality assumption,
best

[Amiira]

Very instructive. It helps me a lot to get a better perspective of things.
Thanks for taking your time to send the links

[Amiira]

@Andrzej One thing is confusing me. According to the paper it says "The central limit theorem means that as sample size gets larger, the more normal the distribution becomes more normal"

I am working with a sample of around 6 million data. Does it mean that my data is supposed to be normal?
Because when I run a Q-Q plot on STATA, I get a skewed data with heavy tail:
Skewness:30.99
Kurtosis:1800

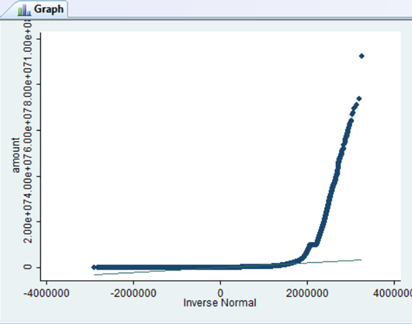
What I would like to add is that for my analysis, it is essential that I know if my data is heavy-tailed and/or skewed. The reason for that is because I have to choose a method to identify outlier
Standard boxplot by (Tukey,1977): Does not account for skewness & heaviness of tail
Adjusted boxplot by(Mia Hubert): Account only for skewness & not the underlying heaviness
Generalized boxplot by(Bruffaerts): Account for BOTH skewness & heaviness of tail>

So, as shown by the QQ plot and the numeric statistics using sample size=6 million, my data is skewed and heavy tailed. I don't really understand why CLT says "The central limit theorem means that as sample size gets larger, the more normal the distribution becomes more normal". Because as you can see my sample of 6 million is like the sample size is approaching infinity, so why is it not normal according to CLT?

Can someone please clarify. Thanks

[nirgrahamuk]

the central limit theorem is about sampling sub populations of your data and recording the means and forming a distribution from those measures; the distribution of those will be normal if you take many such samples ( under some assumptions); this says nothing about the normality of the underlying data that we record the sample means of (again, its about the distribution of the means we recorded).

[Amiira]

Ohh! I think I get it now. So, it means CLT does not relate to what I am doing as I am not sampling subpopulations. Correct?
Thank you @nirgrahamuk

[nirgrahamuk]

I have no idea,
a) what you are overall doing
b) what statistical approaches you wish to take towards that
so I have no way to say if its an issue for you or not...

[Amiira]

Is there a way in STATA to extract boxplot summary made by the command graph box. In R, I know we can, but I'm very new to STATA to it still.

[nirgrahamuk]

I have never used STATA, perhaps there are other forums for advice with that ?

[Amiira]

Ohh it's fine.

In RStudio, we can access the outliers in the variable "out". Is there a way that I can extract the number of outliers in the variable out?

I wanted to extract the total number of outliers in variable out.

[nirgrahamuk]

Use length() to see how many entries are in a variable.

[Amiira]

Can you provide me a link to a STATA forum?

[HanOostdijk]

I think this an intriguing question.
Not because you are asking this on a R forum.
But why do you expect that users of this forum are better equipped than you to search the internet?
Of course: we are good, but so good .... ?

https://www.statalist.org/