I'm working on a Bayesian model and stumbled upon some convergence problems. I am sure that I am making a silly mistake, as I have little formal background in Math. Still, I can't identify the problem so I cannot solve it.
Basically, I am sanity-checking the model by applying it to simulated data, so I can compare with "true" values, before I use actual data. My model was designed to be applied to experiments in Psychophysics. Basically, subjects are presented with a series of four physical properties (named x1, x2, x3, x4). Then, they produce a response that combines such properties. However, in this combination they will give more weight to some properties (e.g., A) than to others. The model should take the responses from the whole sample of participants (one response by participant), and estimate the four coefficients that weight the four observations (Psi1, Psi2, Psi3, and Psi4). To ensure you understand me, this is the program that simulates the data in R:
set.seed(40) #This makes the example reproducible...
psi <- runif(4, 0, 1) #This creates a random set of 4 coefficients between 0 and 1.
x <- c(20, 4, 2, 10) #Vector with the 4 physical properties to be learned
combinedX <- ((psi[1]*x[1])/((psi[1]*x[1])+(psi[2]*x[2]))) - ((psi[3]*x[3])/((psi[3]*x[3])+(psi[4]*x[4])))
#This combination rule is a weighted version of Cramer's Phi coefficient of association. Each property x (x[1], x[2], x[3], x[4]) is multiplied by the corresponding coefficient stored in the vector psi.
n <- 50 #I want to simulate 50 data
data <- rnorm(n, combinedX, 0.1) #And they are obtained from a normal distribution with mean combinedX.
I want now to submit these simulated data to a Bayesian model in JAGS that should take the data vector, and output an estimation of the four coefficients.
model{
psi1 ~ dbeta(1,1)
psi2 ~ dbeta(1,1)
psi3 ~ dbeta(1,1)
psi4 ~ dbeta(1,1)
predx <- ((psi1*x[1])/ ((psi1*x[1])+(psi2*x[2]))) - ((psi3*x[3])/((psi3*x[3])+(psi4*x[4])))
sigma <- exp(log_sigma)
log_sigma ~dunif(-10, 10)
for(i in 1:n){
data[i] ~ dnorm(predx, sigma)
}
}
So, basically, the model only assumes that data come from a normal distribution with mean "predx", which is obtained by combining the four Xs and the four psis.
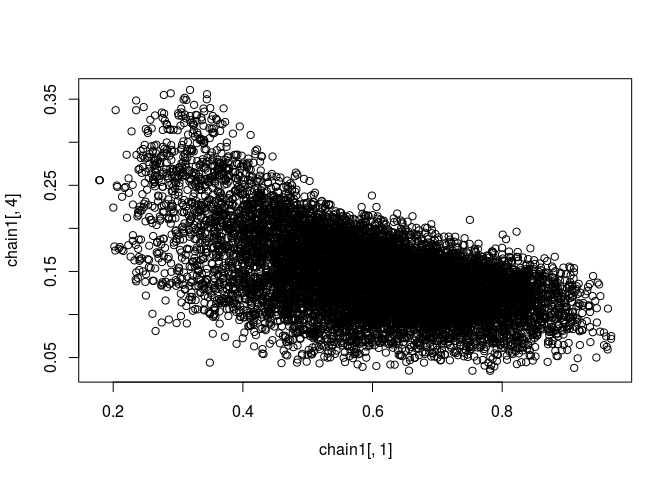
Good. When I run this model, I obtain nonsensical results most of the times, and often detect problems of convergence, chains that do not mix, extremely flat posteriors (maximal uncertainty), or estimations very different from the actual values...
I suspect two reasons for this behavior:
-Autocorrelation. But, how to solve it?
-The problem is ill-defined: we have too many free parameters (4) to be estimated from data.
Any idea as to what to do with this model?
Thank you in advance.