Is there an approach to modify a power law relationship to add a exponent to one of the logged variables?

[dougfir]

I'm working on a model based on a power law. From some research and videos, it looks like when I have a straight line after taking the log of an x and y variable, I can say I have a power law model.

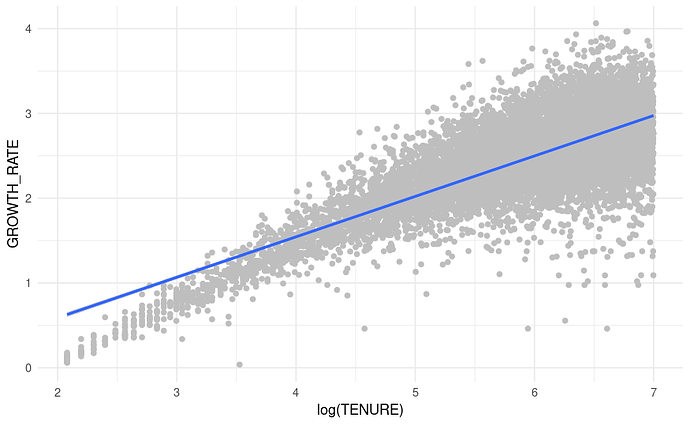
I have an almost straight line but it needs a little curvature of it's own to visually fit better. Here's a plot of log growth rate (Y axis is log even though the axis doesn't say that) and log(tenure) - I'm plotting log cumulative revenue growth for a cohort of customers:

plotd |>
  ggplot(aes(x = log(TENURE), y = GROWTH_RATE)) +
  geom_point(color = 'grey') +
  geom_smooth(method = 'lm', formula = 'y ~ x') +
  theme_minimal()

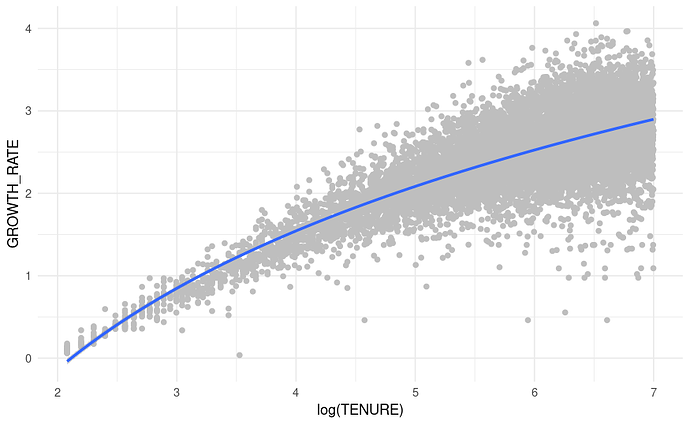
I noticed that if I double log the x axis tenure I get this visual. Since my aes() already takes log(x) , by adding formula = y ~ log(x) in geom_smooth I'm basically double logging (you can perhaps tell I discovered this by accident with a mistake in my r code):

plotd |>
  ggplot(aes(x = log(TENURE), y = GROWTH_RATE)) +
  geom_point(color = 'grey') +
  geom_smooth(method = 'lm', formula = 'y ~ log(x)') +
  theme_minimal()

Just visually, this line appears to fit better.

The geom_smooth fitted line is therefore the log(log(TENURE)) fitted against growth rate.

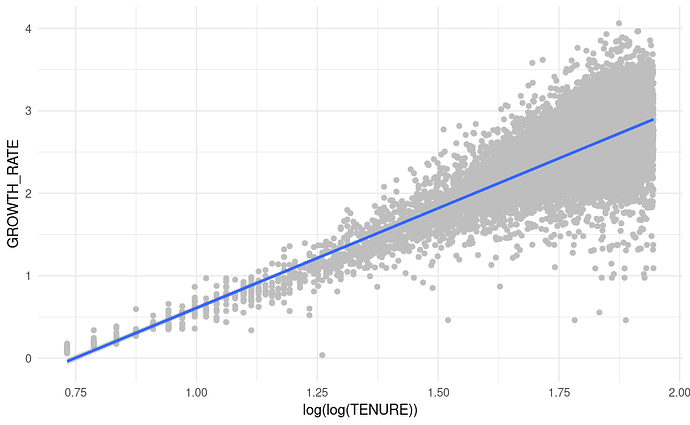
The same plot but taking the log(log(Tenure)) in the aes() from the start:

plotd |> 
  ggplot(aes(x = log(log(TENURE)), y = GROWTH_RATE)) +
  geom_point(color = 'grey') +
  geom_smooth(method = 'lm', formula = 'y ~ x') +
  theme_minimal()

THis indeed looks like a better relationshipt to model. What does this mean?! A log(log(x)) relationship? Do I have a power law relationship or something else? Can I use this newly found relationship to fit a model that would be expected to fit better than the power law model?

[nirgrahamuk]

putting aside the terminology, I'll answer the question. a log(log(x) relationship may be a better fit to data than a log(x) to y, the proof is in the statistics.

Here is an example where data with the relationship in question is artificially constructed. a spoilfactor is used to somewhat randomise the values, set it to zero for purity

set.seed(42)

spoilfactor <- 100 
# spoilfactor <- 0 

(exdf<- data.frame(y=(0:100)/25,
  x= exp(exp((0:100)/25))+rnorm(101,mean = 0,sd= spoilfactor)))


lm1 <- lm(y~log(x),data=exdf)
lm2 <- lm(y~log(log(x)),data=exdf)

summary(lm1)
summary(lm2)


summary(lm2)$r.squared
plot.new()
par(mfrow=c(2,1))
plot(lm1,1)
title(round(summary(lm1)$r.squared,2))
plot(lm2,1)
title(round(summary(lm2)$r.squared,2))

[dougfir]

OK, so using a log(log(x)) is a 'normal' thing to do?! I.e. it's not indicative of some other relationship with some redefined name? It's just a log(log(x)) model?