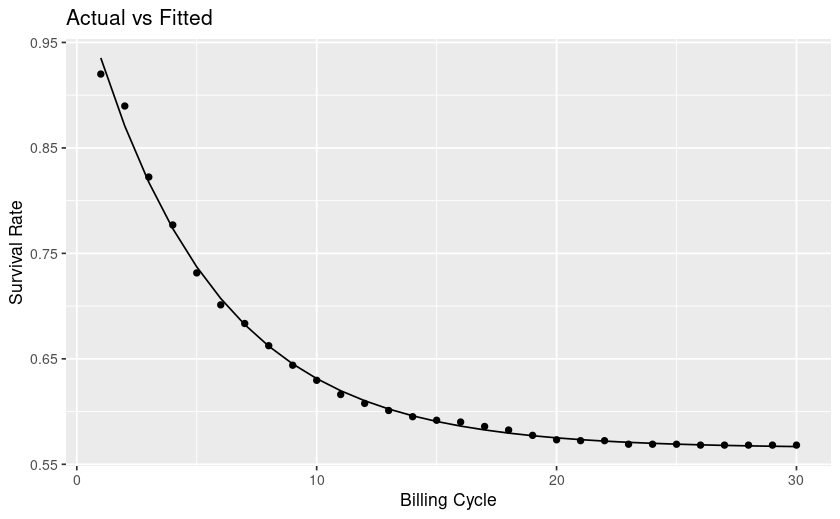
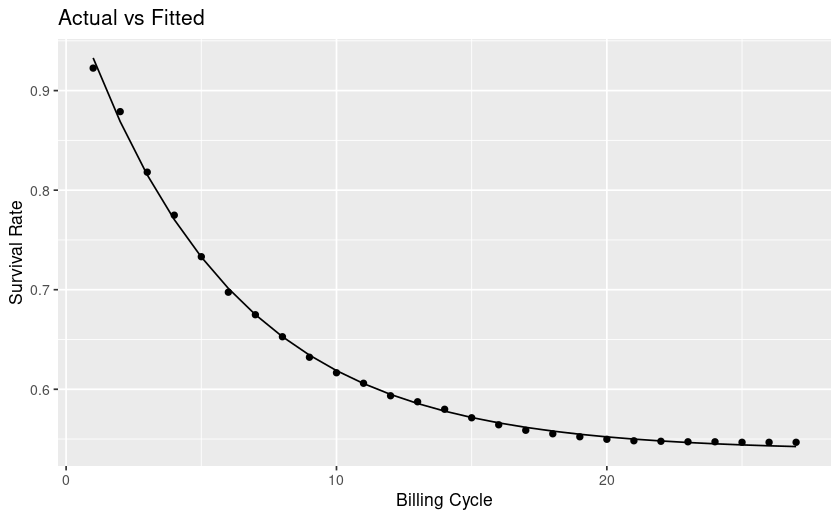
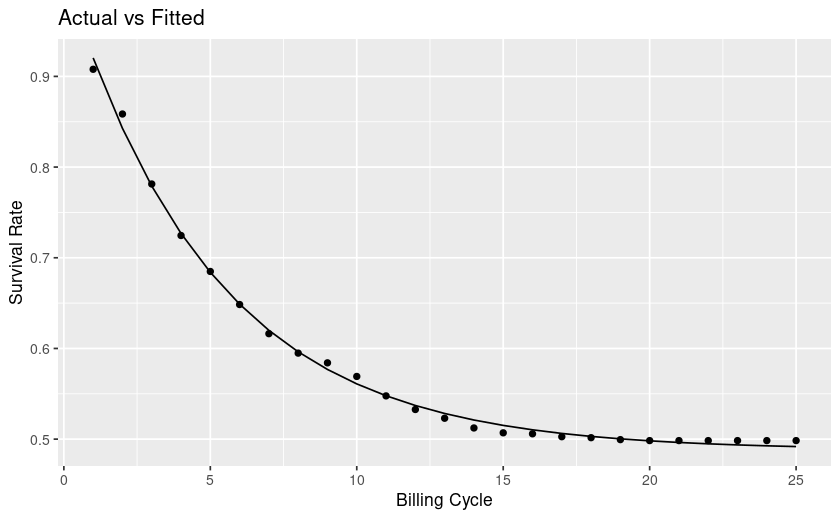
Context is a churn/survival analysis.
I have a Surv object, Kaplan Meier plot and an accompanying Weibul overlaid.
# create a survival object
surv_object <- Surv(time = rawd$billing_cycle, event = rawd$churned)
# fit it to kaplan meir
km_null <- survfit(surv_object ~ 1, data = rawd)
km_plan <- survfit(surv_object ~ plan_family, data = rawd)
# visualize
km_null_plot <- km_null %>% ggsurvplot(data = rawd, conf.int = F)
km_plan_plot <- km_plan %>% ggsurvplot(data = rawd, pval = T)
# weibul with function for overlay
wb <- rawd %>%
group_by(plan_period) %>% # dummy, all are 'Monthly'
nest %>%
mutate(WB = map(.x = data, ~ survreg(Surv(time = billing_cycle, event = churned) ~ 1, data = .x, dist = 'weibull'))) %>%
mutate(SurvWBDF = map(.x = WB, ~ data.frame(surv = seq(.99, .01, by = -.01), upper = NA, lower = NA, std.err = NA) %>%
mutate(time = predict(.x, type = "quantile", p = 1 - surv, newdata = data.frame(1)))))
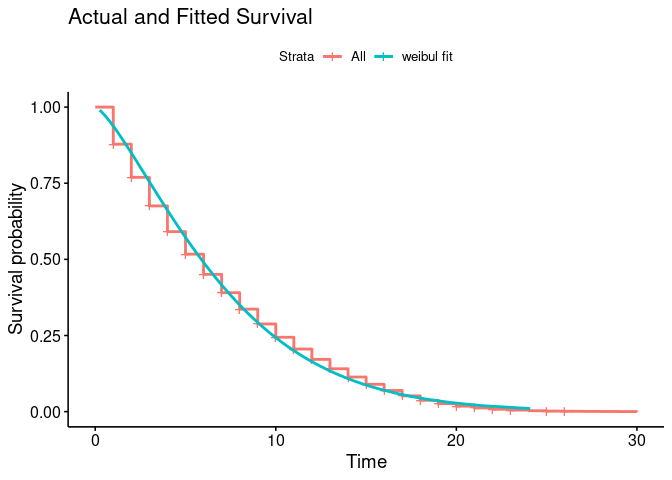
# plot actual and predicted overlay
km_null_plot$plot +
geom_line(data = wb$SurvWBDF[[1]], aes(time, surv, color = 'weibul fit'), size = 1) +
labs(title = "Actual and Fitted Survival")
Produces this plot:
The summary() of the model is:
Call:
survreg(formula = Surv(time = billing_cycle, event = churned) ~
1, data = .x, dist = "weibull")
Value Std. Error z p
(Intercept) 4.0953 0.0814 50.3 < 2e-16
Log(scale) -0.1647 0.0375 -4.4 1.1e-05
Scale= 0.848
Weibull distribution
Loglik(model)= -2538.3 Loglik(intercept only)= -2538.3
Number of Newton-Raphson Iterations: 11
n= 6261
From this I calculated shape or 'k' based on this post thus, where WB is my weibul fit:
Shape = map_dbl(.x = WB, ~ 1 / .x$scale)
Gives me 1.179 shape.
From searching online, e.g. wikipedia:
If the quantity X is a "time-to-failure", the Weibull distribution gives a distribution for which the failure rate is proportional to a power of time. The shape parameter, k
... is that power plus one, and so this parameter can be interpreted directly as follows:
A value of k<1
indicates that the failure rate decreases over time. This happens if there is significant "infant mortality", or defective items failing early and the failure rate decreasing over time as the defective items are weeded out of the population. In the context of the diffusion of innovations, this means negative word of mouth: the hazard function is a monotonically decreasing function of the proportion of adopters;
A value of k=1
indicates that the failure rate is constant over time. This might suggest random external events are causing mortality, or failure. The Weibull distribution reduces to an exponential distribution;
A value of k>1
indicates that the failure rate increases with time. This happens if there is an "aging" process, or parts that are more likely to fail as time goes on. In the context of the diffusion of innovations, this means positive word of mouth: the hazard function is a monotonically increasing function of the proportion of adopters. The function is first concave, then convex with an inflexion point at (e1/k−1)/e1/k,k>1
From looking at my plot my curve levels off, at future timepoints the rate of survival is mostly flat, whereas towards the left it's steep and thus churn is high. This interpretation is counter to the explanations I find online.
Have I misinterpreted, does my shape look correct for this curve? How can I interpret it? Do people churn more or less with time?