How to use Kelly Criterion to place an order in financial market

General
1

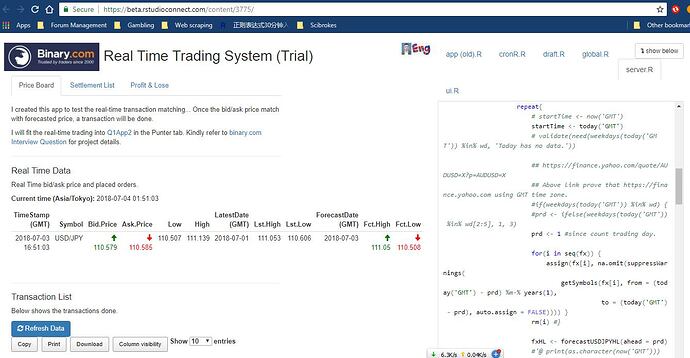
I tried to write a real-time trading system, however do not know how to fit a Kelly model into the system. The system will automatically calculate everyday 12AM while I want to add another function which is auto placed order with certain stakes (by applied Kelly criterion model) once got the calculated forecast price.

1340×697 114 KB

Source Code：Real Time Trading System (Trial)

Below coding is that I tried to use looping to calculate the data history, calculate the staking, profit & lose, and also bankroll.

...
...
...
  ## merge dataset
  fitm <- cbind(fit1, forClose = fit2$Point.Forecast) %>% tbl_df
  
  ## convert to probability.
  fitm %<>% mutate(ProbB = pnorm(Point.Forecast, mean = forClose, sd = sd(forClose)), 
                   ProbS = 1 - ProbB) #ProbS = pnorm(Point.Forecast, mean = forClose, sd = sd(forClose), lower.tail = FALSE)
  
  ## The garch staking models (Kelly criterion) P&L column.
  ## staking model and bankroll management.
  ## need to refer to Niko Martinen's fund management formula to maximise the stakes and profit base on Kelly models.
  ## https://github.com/scibrokes/betting-strategy-and-model-validation/blob/master/references/Creating%20a%20Profitable%20Betting%20Strategy%20for%20Football%20by%20Using%20Statistical%20Modelling.pdf
  #.... dynamic staking model need to adjusted based on updated bankroll but not portion of fixed USD100 per bet.
  fitm %<>% mutate(BR = .initialFundSize) %>% 
    #'@ mutate(Return.Back = ifelse(Prob > 0.5, Diff * Back * stakes, 0), 
    #'@        Return.Lay = ifelse(Prob < 0.5, -Diff * Lay * stakes, 0))
    mutate(fB = 2 * ProbB - 1, fS = 2 * ProbS - 1, 
           EUB = ProbB * log(BR * (1 + fB)) + (1 - ProbB) * log(BR * (1 - fB)), 
           EUS = ProbS * log(BR * (1 + fS)) + (1 - ProbS) * log(BR * (1 - fS)), 
           #'@ Edge = ifelse(f > 0, EUB, EUS), #For f > 0 need to buy and f <= 0 need to sell.
           #need to study on the risk management on "predicted profit" and "real profit".
           Edge = ifelse(fB > 0, EUB, ifelse(fS > 0, EUS, 0)), 
           PF = ifelse(Point.Forecast >= USDJPY.Low & 
                         Point.Forecast <= USDJPY.High, 
                       Point.Forecast, 0), #if forecasted place-bet price doesn't existing within Hi-Lo price, then the buying action is not stand. Assume there has no web bandwith delay.
           FC = ifelse(forClose >= USDJPY.Low & forClose <= USDJPY.High, 
                       forClose, USDJPY.Close), #if forecasted settle price doesn't existing within Hi-Lo price, then the closing action at closing price. Assume there has no web bandwith delay.
           #'@ Diff = round(forClose - USDJPY.Close, 2),
           ##forecasted closed price minus real close price.
           
           Buy = ifelse(PF > 0 & FC > PF, 1, 0), ##buy action
           Sell = ifelse(PF > 0 & FC < PF, 1, 0), ##sell action
           BuyS = Edge * Buy * (forClose - PF), 
           SellS = Edge * Sell * (PF - forClose), 
           Profit = BuyS + SellS, Bal = BR + Profit)
  
  #'@ fitm %>% dplyr::select(Point.Forecast, forClose, Prob, BR, f, EU, Edge, PF, FC, Buy, Sell, SP, Bal)
  #'@ fitm %>% dplyr::select(ProbB, ProbS, BR, fB, fS, EUB, EUS, Edge, PF, USDJPY.Open, FC, Buy, Sell, BuyS, SellS, Profit, Bal) %>% filter(PF > 0, FC > 0)
  
  ## The garch staking models (Kelly criterion) Adjusted Banl-roll and Balance column.
  for(i in seq(2, nrow(fitm))) {
    fitm$BR[i] = fitm$Bal[i - 1]
    fitm$fB[i] = 2 * fitm$ProbB[i] - 1
    fitm$fS[i] = 2 * fitm$ProbS[i] - 1
    fitm$EUB[i] = fitm$ProbB[i] * log(fitm$BR[i] * (1 + fitm$fB[i])) + 
      (1 - fitm$ProbB[i]) * log(fitm$BR[i] * (1 - fitm$fB[i]))
    fitm$EUS[i] = fitm$ProbS[i] * log(fitm$BR[i] * (1 + fitm$fS[i])) + 
      (1 - fitm$ProbS[i]) * log(fitm$BR[i] * (1 - fitm$fS[i]))
    fitm$Edge[i] = ifelse(fitm$fB[i] > 0, fitm$EUB[i], 
                          ifelse(fitm$fS[i] > 0, fitm$EUS[i], 0)) #For f > 0 need to buy and f <= 0 need to sell.
    #need to study on the risk management on "predicted profit" and "real profit".
    
    fitm$BuyS[i] = fitm$Edge[i] * fitm$Buy[i] * (fitm$forClose[i] - fitm$PF[i])
    fitm$SellS[i] = fitm$Edge[i] * fitm$Sell[i] * (fitm$PF[i] - fitm$forClose[i])
    fitm$Profit[i] = fitm$BuyS[i] + fitm$SellS[i]
    fitm$Bal[i] = fitm$BR[i] + fitm$Profit[i]
    #'@ if(fitm$Bal[i] <= 0) stop('All invested fund ruined!')
  }; rm(i)
  
  names(mbase) <- str_replace_all(names(mbase), '^(.*?)+\\.', nm)
  
  if(.filterBets == TRUE) {
    fitm %<>% filter(PF > 0, FC > 0)
  }
  
  fitm %<>% mutate(RR = Bal/BR)
  
  ## convert the log leverage value of fund size and profit into normal digital figure with exp().
  if(.fundLeverageLog == TRUE) fitm %<>% 
    mutate(BR = exp(BR), BuyS = exp(BuyS), SellS = exp(SellS), 
           Profit = exp(Profit), Bal = exp(Profit))
  
  return(fitm)

Source Code：simStakesGarch.R

Reference