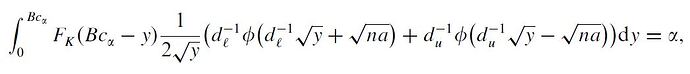Hi everyone,
I am the newcomer and trying to solve a math expression that have two variables, ca and y , and actually I only want to know the value of variable ca because the variable y will be integrated like the code below:
#---time start---#
ptm <- proc.time()
library(pracma)
U = 14; L = 7; d = (U-L)/2;
T = ( 3*U+L )/(3+1); # by 3Du = Dl
Du = U-T; Dl = T - L; d_star = min(Du,Dl);
du = d/Du; dl = d/Dl;
alpha = 0.05;
aLe = 0.05;
n = 100;
ksi_given = -3;
if (ksi_given <= 0){
sigma = fzero(function(x) aLe - (x^2)*( (dl^2*ksi_given^2+1)/d_star^2 ), c(0,0.5) )$x ;
mu = ksi_given*sigma + T;
B = n*( (dl*ksi_given)^2 + 1 )/aLe;
C = (dl*ksi_given)^2/(d_star/sigma)^2 + 1/(d_star/sigma)^2;
b = d_star/sigma;
}else{
sigma = fzero(function(x) aLe - (x^2)*( (du^2*ksi_given^2+1)/d_star^2 ), c(0,0.5) )$x ;
mu = ksi_given*sigma + T;
B = ( n*( (du*ksi_given)^2 + 1 ) )/aLe;
C = (du*ksi_given)^2/(d_star/sigma)^2 + 1/(d_star/sigma)^2;
b = d_star/sigma;
}
fun = function(ca,y) { pchisq( B*ca-y, n-1)* ( 1/ (2*sqrt(y)) )* ( (dl^-1)*normpdf( (dl^-1)*sqrt(y) + sqrt(n*ksi_given) ) + (du^-1)*normpdf( (du^-1)*sqrt(y) - sqrt(n*ksi_given) ) ) };
fun2 = function(ca) alpha - integrate(fun(ca,y),lower = 0.0001,upper = B*ca);
c = linspace(1e-4,0.1,100);
for (i in 1:numel(c)){
fc(i) = fun2(c(i));
}
plot(c,fc)
ca = fzero(function(ca) fun2, aLe);
About the expression that I will use fzero() to solve, it is created by these steps:
- There is an originally expression fun which has two variables, ca and y.
- I will use integrate() to integrate fun about the variable y, and then get the fun2 .
Finally, I will try to use fzero() to solve the value of ca in fun2 like my last line of code.
Unfortunately, R return the error message like this:
Error in pchisq(B * ca - y, n - 1) : argument "y" is missing, with no default
I have also tried this modifying code
ca = fzero(function(ca) alpha - integrate({ pchisq( B*ca-y, n-1)* ( 1/ (2*sqrt(y)) )* ( (dl^-1)*normpdf( (dl^-1)*sqrt(y) + sqrt(n)*(ksi_given) ) + (du^-1)*normpdf( (du^-1)*sqrt(y) - sqrt(n)*(ksi_given) ) ) },lower = 0.0001,upper = B*ca), aLe);
but it doesn't work.
Does anyone can give me some advice about my problem to correctly get the value of ca?
Does it mean pchisq() could not using variables as its parameters? or I have misunderstand the usage of function() or integrate() or fzero()?
Hope you can give me some advice! Thanks!