How to plot a Random walk in 2D ?

[Kevser_Cifci]

Hello!

I'm trying to write a code on a random walk in 2d. This random walk is biased: the probability to choose the next step (vertex) depends on the number of time the walker has already chosen this vertex.

Next_step = function(i,j,Grille){
  
    l = nrow(Grille)
    prob = rep(NA,4)
  
    prob[1] = Grille[i+1,j]/(Grille[i,j-1]+Grille[i,j+1]+Grille[i-1,j]+Grille[i+1,j])
    prob[2] = Grille[i,j+1]/(Grille[i,j-1]+Grille[i,j+1]+Grille[i-1,j]+Grille[i+1,j])
    prob[3] = Grille[i,j-1]/(Grille[i,j-1]+Grille[i,j+1]+Grille[i-1,j]+Grille[i+1,j])
    prob[4] = Grille[i-1,j]/(Grille[i,j-1]+Grille[i,j+1]+Grille[i-1,j]+Grille[i+1,j])
    next_step = sample(1:4, 1,replace = TRUE, prob = prob)
  

    if (next_step == 1) { # en bas
      i = i+1
    } else if (next_step == 2) {  # à droite 
      j = j+1
    } else if (next_step == 3) { # à gauche
      j= j-1
    } else if (next_step == 4) { # en haut 
      i = i-1
    }
  return(c(i,j))
}


RW_2d = function(nRow,nCol,pas){
  
  #nRow = 6
  #nCol = 6
  
  Grille = matrix(1, nrow = nRow+2, ncol = nCol+2)
  Grille[c(1,nRow+2),] = 0
  Grille[,c(1,nRow+2)]=0
  
  axe_x = rep(NA,pas)
  axe_y = rep(NA,pas)
  d = rep(NA,2)
  
  axe_x[1] = sample(1:nRow,1)
  axe_y[1] = sample(1:nCol,1)
  Grille[axe_x[1],axe_y[1]] = Grille[axe_x[1],axe_y[1]]+1
  for (i in 2:pas){ 
    d[1:2]= Next_step(axe_x[i-1],axe_y[i-1],Grille) 
    axe_x[i]=d[1] 
    axe_y[i]=d[2] 
    Grille[d[1],d[2]] = Grille[d[1],d[2]]+1
  }
  plot(axe_x,axe_y,type = 'l')
  return(Grille)
}

I want to plot this with colors like in this image but I don't know how?

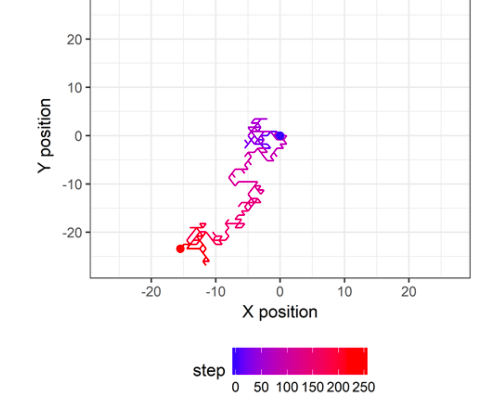
Does anyone have an idea?

Moreover, how can I represent the number of passages by each vertex with "heat map" or another function?

Thank you !

[AlexisW]

For plotting, the best is to have the function RW_2d() return the data, rather than plotting inside the function. So I changed the last two rows from

plot(axe_x,axe_y,type = 'l')
return(Grille)

To just

return(list(path = data.frame(step = seq_along(axe_x), x = axe_x, y = axe_y),
              Grille = Grille))

So now I can run the function:

res <- RW_2d(50,50,250)

This is a list containing, first, a data.frame with the path followed. We can use it to plot. I couldn't figure out how to plot the colors properly with base graphics (though I'm sure it's possible), but it's easy enough using {ggplot2} (needs to be installed):

res_path <- res$path
ggplot(res_path) +
  theme_classic() +
  geom_path(aes(x = x, y = y, color = step)) +
  scale_color_steps(low = "blue",
                    high = "red")

And for the grid:

image(res$Grille)

Or a potentially better-looking representation:

pheatmap::pheatmap(res$Grille,
                   cluster_rows = FALSE,
                   cluster_cols = FALSE)

(requires the package {pheatmap})

[Kevser_Cifci]

thank you this is very helpful !