Hello
I want to get results with below codes that is based on Spearman rank correlation. Could someone kindly help me to modify them for Spearman rank correlation. The results with below codes used Pearson correlation. Thanks
library("PerformanceAnalytics")
mydata<- read.csv("Correlation.csv", TRUE, ",")
mydata[,sapply(mydata,is.numeric)]
data=mydata[,sapply(mydata,is.numeric)]
my_data=as.matrix(data)
chart.Correlation(my_data, histogram = TRUE, pch = 19)
You can use the cor() function from the stats package.
cor_result <- cor(x, y, method = "spearman")
You can specify what to do if you have missing data using the "use" argument.
Thanks for the comments. Can you kindly insert this line into my codes?
That's hard to do since I don't have a reprex of your dataset (the PerformanceAnalytics package doesn't have access to "Correlation.csv"). However, from what I can see, you want to do a correlation matrix, not just a correlation of two variables? If so, you may want to check out this blog post regarding correlation tests, matrices and visualizations.
https://rstudio-pubs-static.s3.amazonaws.com/240657_5157ff98e8204c358b2118fa69162e18.html
I have several variables and that's why I couldn't find the solution. Here is a link to my data if you want.
https://drive.google.com/file/d/1Gj5IllOIu7PbSp09Mya4rkp1dj8taGMX/view?usp=sharing
Hi Umar,
I tried the example for function chart.Correlation(), it seems that the option parameter 'method = ...' does not work! So, all in all only correlation calcualtion based on 'pearson' is possible. I think it's may a bug in the function. I will see how the code works... 
Best regards
Adam
If that is the case; can we modify the codes of PCA that is also based on Pearson to Spearman rank correlation.
library("FactoMineR")
library("factoextra")
mydata<- read.csv("Correlation.csv", TRUE, ",")
mydata[is.na(mydata)]=0
attach(mydata)
X=cbind (AMBI, BENTX, Chl.a, Diversity, DO, M.AMBI, Temp, TOC, TUBI)
summary(X)
cor(X)
res.pca <- princomp(X, scores=TRUE, cor=TRUE)
summary(res.pca)
fviz_pca_var(res.pca, col.var="contrib",
gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"),
repel = TRUE, # Avoid text overlapping
axes = c(1, 2) # choose PCs to plot
)
Could you please turn this into a self-contained REPRoducible EXample (reprex)? A reprex makes it much easier for others to understand your issue and figure out how to help.
If you've never heard of a reprex before, you might want to start by reading this FAQ:
As Andrés mentioned before, please, try to use 'reprex ' (FAQ ) in future. It's a cool tool to post your questions to the R-communtiy. It helps us to help you! 
Based on your first request a possible solution in a reprex
library(PerformanceAnalytics)
data(managers)
head(managers[,1:4], n = 10)
#> HAM1 HAM2 HAM3 HAM4
#> 1996-01-31 0.0074 NA 0.0349 0.0222
#> 1996-02-29 0.0193 NA 0.0351 0.0195
#> 1996-03-31 0.0155 NA 0.0258 -0.0098
#> 1996-04-30 -0.0091 NA 0.0449 0.0236
#> 1996-05-31 0.0076 NA 0.0353 0.0028
#> 1996-06-30 -0.0039 NA -0.0303 -0.0019
#> 1996-07-31 -0.0231 NA -0.0337 -0.0446
#> 1996-08-31 0.0395 -0.0001 0.0461 0.0351
#> 1996-09-30 0.0147 0.1002 0.0653 0.0757
#> 1996-10-31 0.0288 0.0338 0.0395 -0.0180
#modified function chart.Correlation2(...)
chart.Correlation2 <- function (R, histogram = TRUE, method = NULL, ...){
x = checkData(R, method = "matrix")
if (is.null(method)) #modified
method = 'pearson'
use.method <- method #added
panel.cor <- function(x, y, digits = 2, prefix = "", use = "pairwise.complete.obs",
method = use.method, cex.cor, ...) { #modified
usr <- par("usr")
on.exit(par(usr))
par(usr = c(0, 1, 0, 1))
r <- cor(x, y, use = use, method = method)
txt <- format(c(r, 0.123456789), digits = digits)[1]
txt <- paste(prefix, txt, sep = "")
if (missing(cex.cor))
cex <- 0.8/strwidth(txt)
test <- cor.test(as.numeric(x), as.numeric(y), method = method)
Signif <- symnum(test$p.value, corr = FALSE, na = FALSE,
cutpoints = c(0, 0.001, 0.01, 0.05, 0.1, 1), symbols = c("***",
"**", "*", ".", " "))
text(0.5, 0.5, txt, cex = cex * (abs(r) + 0.3)/1.3)
text(0.8, 0.8, Signif, cex = cex, col = 2)
}
f <- function(t) {
dnorm(t, mean = mean(x), sd = sd.xts(x))
}
dotargs <- list(...)
dotargs$method <- NULL
rm(method)
hist.panel = function(x, ... = NULL) {
par(new = TRUE)
hist(x, col = "light gray", probability = TRUE, axes = FALSE,
main = "", breaks = "FD")
lines(density(x, na.rm = TRUE), col = "red", lwd = 1)
rug(x)
}
if (histogram)
pairs(x, gap = 0, lower.panel = panel.smooth, upper.panel = panel.cor,
diag.panel = hist.panel)
else pairs(x, gap = 0, lower.panel = panel.smooth, upper.panel = panel.cor)
}
#if method option not set default is 'pearson'
chart.Correlation2(managers[,1:4], histogram=TRUE, pch="19")
chart.Correlation2(managers[,1:4], histogram=TRUE, pch="19", method = 'spearman')
#> Warning in cor.test.default(as.numeric(x), as.numeric(y), method = method):
#> Cannot compute exact p-value with ties
Created on 2019-03-15 by the reprex package (v0.2.1)
It's not an answer to your question, but can you please tell why do you want to use spearman instead of pearson?
princomp can take the correlation matrix as an argument. So, I suppose you can modify your suitably by making correlation matrix before doing PCA. Check below:
dataset <- iris[, -5]
correlation_matrix_pearson <- cor(x = dataset,
method = "pearson")
correlation_matrix_spearman <- cor(x = dataset,
method = "spearman")
PCA_pearson <- princomp(covmat = correlation_matrix_pearson)
PCA_spearman <- princomp(covmat = correlation_matrix_spearman)
PCA_pearson
#> Call:
#> princomp(covmat = correlation_matrix_pearson)
#>
#> Standard deviations:
#> Comp.1 Comp.2 Comp.3 Comp.4
#> 1.7083611 0.9560494 0.3830886 0.1439265
#>
#> 4 variables and NA observations.
PCA_spearman
#> Call:
#> princomp(covmat = correlation_matrix_spearman)
#>
#> Standard deviations:
#> Comp.1 Comp.2 Comp.3 Comp.4
#> 1.6955947 0.9531051 0.4034624 0.2318784
#>
#> 4 variables and NA observations.
Created on 2019-03-15 by the reprex package (v0.2.1)
Thanks. But still the results are in Pearson not in Spearman. Also, the PCA graph changes from circular shape to open square shape.
Thanks dear Adam Skubala. I try to edit my above-mentioned codes but it gives error.
Best regards,
Umar
The edited codes are:
library("FactoMineR")
library("factoextra")
mydata<- read.csv("Correlation.csv", TRUE, ",")
mydata[is.na(mydata)]=0
attach(mydata)
X=cbind (AMBI, BENTX, Chl.a, Diversity, DO, M.AMBI, Temp, TOC, TUBI)
summary(X)
cor(X)
correlation_matrix_spearman <- cor(x = X,
method = "spearman")
res.pca <- princomp(x = correlation_matrix_spearman)
summary(res.pca)
fviz_pca_var(res.pca, col.var="contrib",
gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"),
repel = TRUE, # Avoid text overlapping
axes = c(1, 2) # choose PCs to plot
)
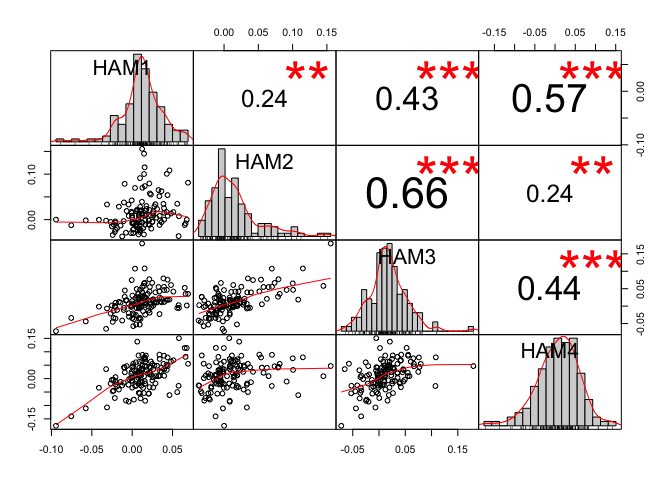
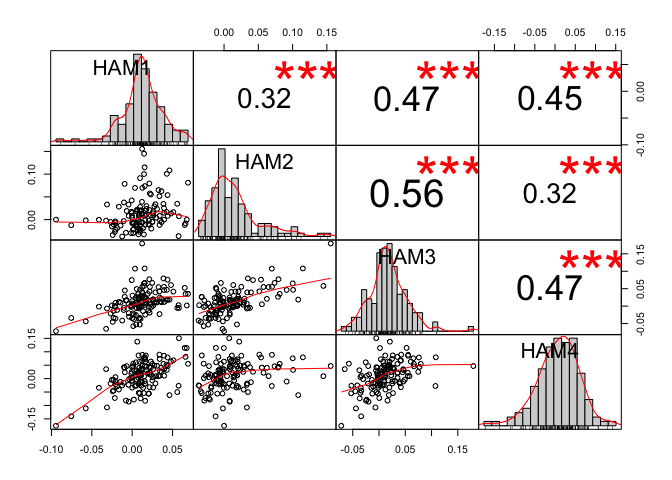
Based on your dataset, I get the following:
library(package = "factoextra")
#> Loading required package: ggplot2
#> Welcome! Related Books: `Practical Guide To Cluster Analysis in R` at https://goo.gl/13EFCZ
dataset <- data.frame(Diversity = c(0.389838802, 1.459984531, 1.30710657, 0.695594724,
-1.138940812, -2.514842465, 0.695594724,
0.389838802, -0.374551005, 0.542716763, -0.374551005,
-0.068795083, -0.833184889, 0.848472686, -1.444696735,
0.848472686, 0.848472686, -0.068795083, -0.527428967,
-0.680306928),
AMBI = c(1.799252377, 0.777842731, 1.092122622, -0.793556725,
-0.872126698, 2.584952105, -1.029266644,
1.170692595, -0.164996943, -1.029266644, -0.243566916,
-0.714986753, -0.400706861, -0.243566916, -0.007856997,
-0.400706861, -0.243566916, 0.306422894, -0.714986753,
-0.872126698),
M_AMBI = c(-0.026636154, -0.026636154, 1.038809999, 1.038809999,
-1.624805383, -2.690251535, 0.506086922,
-0.55935923, -0.026636154, 0.506086922, 1.571533075, 0.506086922,
-0.55935923, 0.506086922, -1.092082306, 1.038809999,
0.506086922, -0.55935923, -0.026636154, -0.026636154),
TUBI = c(-0.46236525, -0.995863616, 0.426798692, 0.960297058,
-0.640198039, -1.529361981, 1.138129846,
0.604631481, 1.138129846, 1.315962635, 0.604631481, 0.782464269,
-0.284532462, -1.70719477, -1.70719477, 0.960297058,
0.071133115, -0.995863616, 0.604631481, -0.284532462),
BENTX = c(-1.658481729, -2.28432389, -1.479669682, -0.585609451,
1.023698965, 1.023698965, 1.023698965, 1.023698965,
0.219044757, 1.023698965, -0.675015474, -0.227985359,
1.023698965, 0.129638734, -0.138579336, 0.397856803,
-0.496203428, -0.406797405, 1.023698965, 0.04023271),
Temp = c(-3.601227684, 0.037718227, 0.037718227, 0.037718227,
0.037718227, -1.257107112, -1.257107112,
0.359072828, 0.359072828, 0.359072828, 0.359072828, 0.573067567,
0.573067567, 0.573067567, 0.573067567, 0.489348348,
0.489348348, 0.489348348, 0.489348348, 0.27861403),
DO = c(2.259516253, 2.259516253, 2.259516253, -0.311202851,
-0.311202851, 0.15011693, 0.15011693, -0.565351111,
-0.565351111, -0.565351111, -0.565351111,
-0.535109028, -0.535109028, -0.535109028, -0.535109028,
-0.504959428, -0.504959428, -0.504959428, -0.504959428,
-0.034698648),
TOC = c(1.075677765, 0.13235778, 1.583710696, -0.530378823,
1.152747528, 2.1278838, -1.097452336, 0.943481828,
0.199056672, -0.781167058, 0.360638279, -0.958518701,
-0.612067376, -0.004827845, -0.612067376, -1.193115427,
-1.193115427, 0.605099292, -1.193115427,
-0.004827845),
Chl_a = c(-0.096498665, -0.096498665, -0.096498665, -0.502949312,
-0.502949312, -0.160138841, -0.160138841,
-0.258498143, -0.258498143, -0.258498143, -0.258498143,
-0.771710385, -0.771710385, -0.771710385, -0.771710385,
1.824941493, 1.824941493, 1.824941493, 1.824941493,
-1.563259561))
correlation_matrix_pearson <- cor(x = dataset,
method = "pearson")
correlation_matrix_spearman <- cor(x = dataset,
method = "spearman")
PCA_pearson <- princomp(covmat = correlation_matrix_pearson)
PCA_spearman <- princomp(covmat = correlation_matrix_spearman)
PCA_pearson
#> Call:
#> princomp(covmat = correlation_matrix_pearson)
#>
#> Standard deviations:
#> Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7
#> 1.8208966 1.5987484 1.0082677 0.9331524 0.7267676 0.5200717 0.4542649
#> Comp.8 Comp.9
#> 0.4032037 0.2708624
#>
#> 9 variables and NA observations.
PCA_spearman
#> Call:
#> princomp(covmat = correlation_matrix_spearman)
#>
#> Standard deviations:
#> Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7
#> 1.6668773 1.5778042 1.1403007 0.9679142 0.8827371 0.5872683 0.4126256
#> Comp.8 Comp.9
#> 0.3576338 0.2695174
#>
#> 9 variables and NA observations.
plot(x = PCA_pearson)
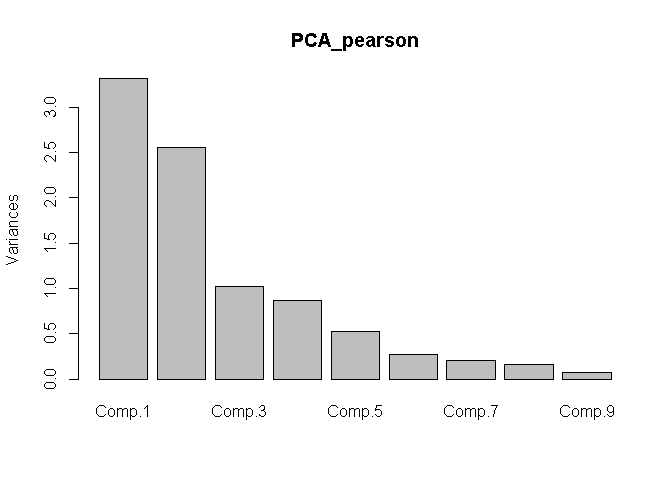
plot(x = PCA_spearman)
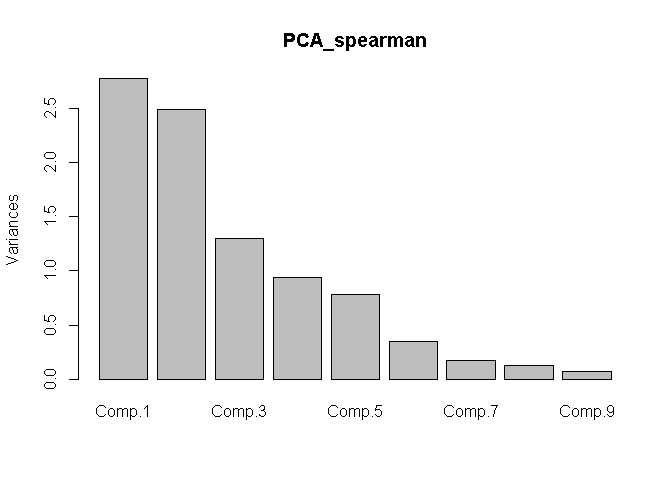
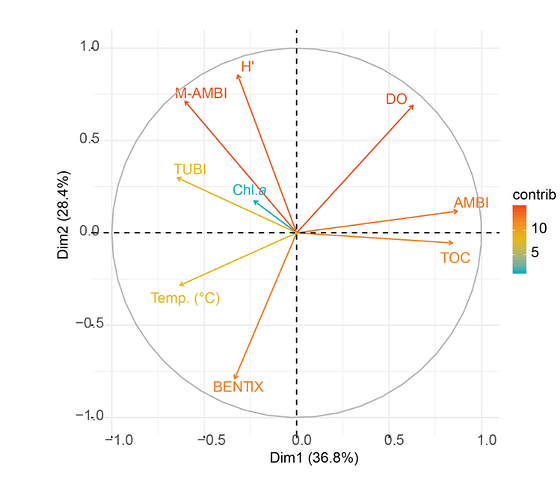
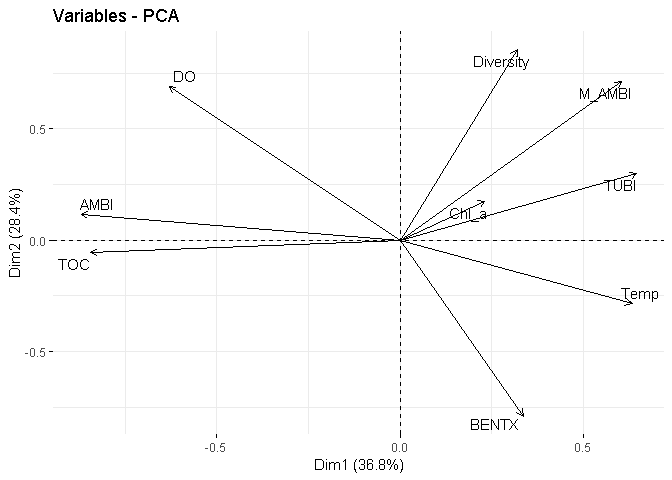
fviz_pca_var(X = PCA_pearson,
repel = TRUE)
fviz_pca_var(X = PCA_spearman,
repel = TRUE)
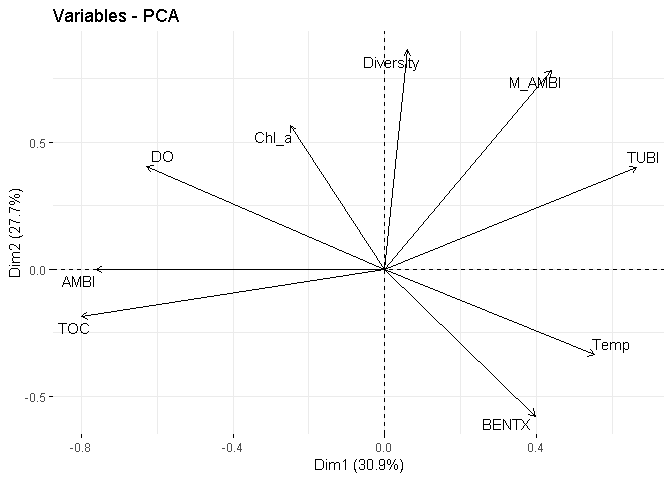
Created on 2019-03-15 by the reprex package (v0.2.1)
Thanks Anirban Ray. It works 
This topic was automatically closed 7 days after the last reply. New replies are no longer allowed.
If you have a query related to it or one of the replies, start a new topic and refer back with a link.