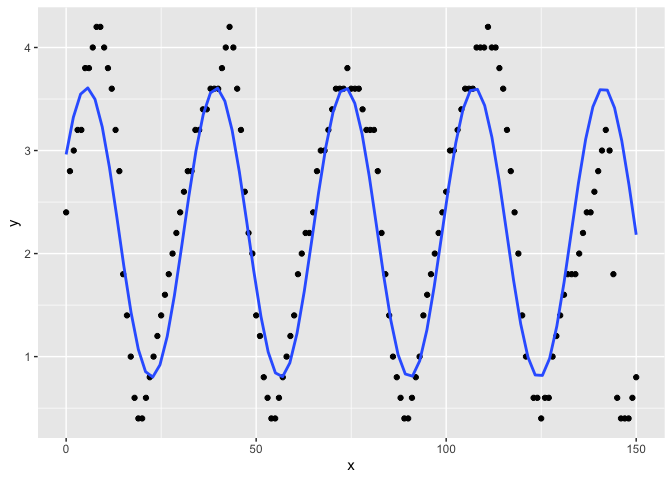
Hi, I am learning R as a Physics student on university. We were given data to plot and calculate a phase difference of 2 data points. The code for one of these data points is shown below (Sorry its very long). I would like to know how to approximate a curve for these data points, usually we're told to plot a linear model which is very easy to do, but for a curve like this I am struggling. Any kind of help will be appreciated!
x<-c(0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150)
y<-c(2.4,2.8,3.0,3.2,3.2,3.8,3.8,4.0,4.2,4.2,4.0,3.8,3.6,3.2,2.8,1.8,1.4,1.0,0.6,0.4,0.4,0.6,0.8,1.0,1.2,1.4,1.6,1.8,2.0,2.2,2.4,2.6,2.8,2.8,3.2,3.2,3.4,3.4,3.6,3.6,3.6,3.8,4.0,4.2,4.0,3.6,3.2,2.6,2.2,2.0,1.4,1.2,0.8,0.6,0.4,0.4,0.6,0.8,1.0,1.2,1.4,1.8,2.0,2.2,2.2,2.4,2.8,3.0,3.0,3.2,3.4,3.6,3.6,3.6,3.8,3.6,3.6,3.6,3.4,3.2,3.2,3.2,2.8,2.2,1.8,1.4,1.0,0.8,0.6,0.4,0.4,0.6,0.8,1.0,1.4,1.6,1.8,2.0,2.2,2.4,2.6,3.0,3.0,3.2,3.4,3.6,3.6,3.6,4.0,4.0,4.0,4.2,4.0,4.0,3.8,3.6,3.2,2.8,2.4,2.0,1.4,1.0,0.6,0.6,0.4,0.6,0.6,1.0,1.2,1.4,1.6,1.8,1.8,1.8,2.0,2.2,2.4,2.4,2.6,2.8,3.0,3.2,3.0,1.8,0.6,0.4,0.4,0.4,0.6,0.8)
plot(x, y, main = 'Short Circuit Position vs Standing Wave Amplitude', xlab="Stadning Wave Position (cm)",
ylab="Amplitude (V)",
bty="l", cex=0.8, pch=16, ylim=c(0,5),
xlim=c(0,150))
y.error<-c(rep(0.2,times=150))
x.error<-c(rep(0.1,times=150))
segments(x, y-y.error, x, y+y.error)
segments(x-x.error, y, x+x.error, y)