I think that the data is insufficient to do more than simulate very vague predictions of possible s-curves.
a lot more data would be required to pick curves of best fit.
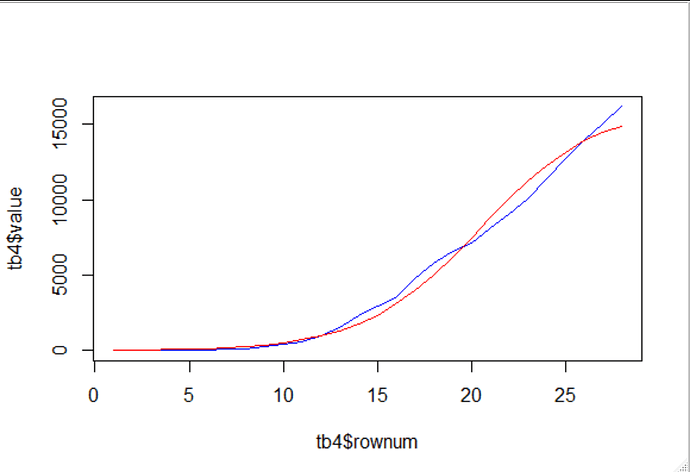
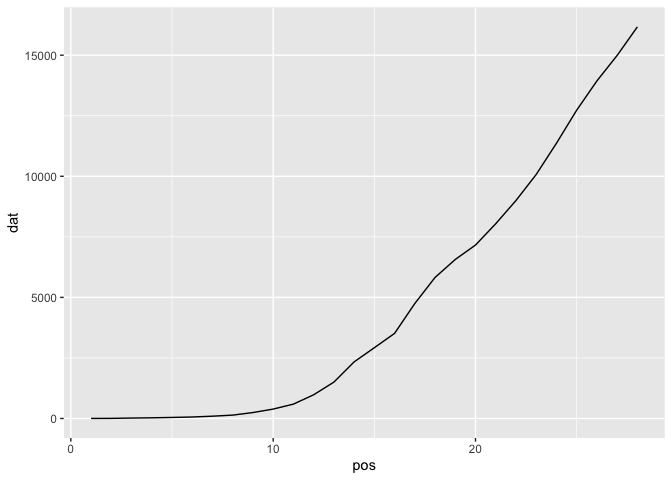
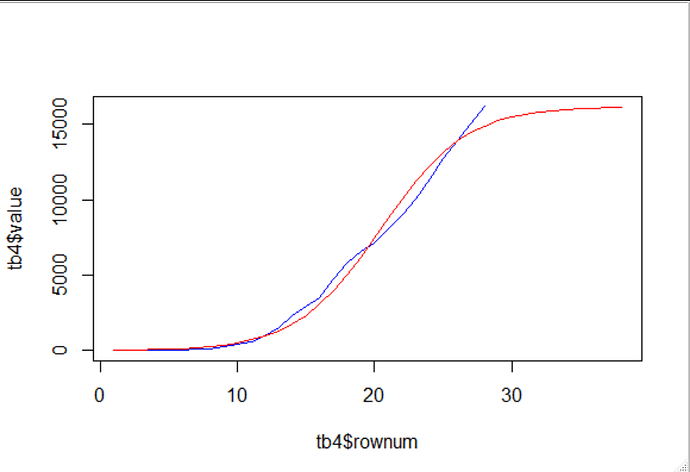
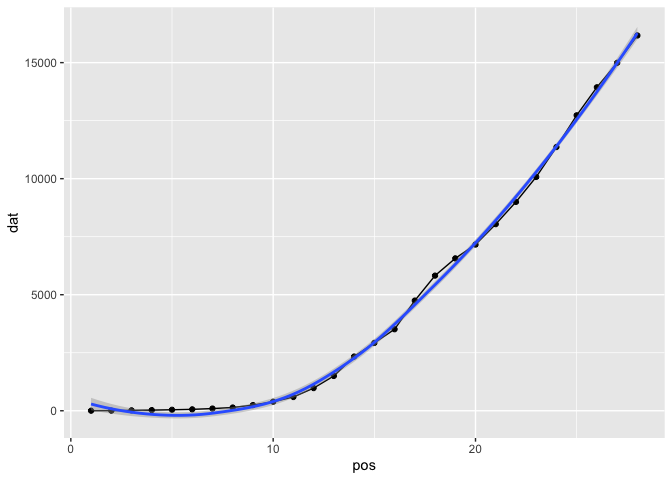
What I'm about to present, is probably flawed, and I'd appreciate help with corrections. I figure that the data presented is very very early in any possible s curve. i.e. theres no sight yet of the inflexion point, so a huge range of possible s-curves can be fit. It seems to me that the fact that only the early portion of an s - curve has been provided can be achieved by dividing linearly the sample values, by some factor that represents how small of a portion of an s-curve has been presented. Then we can try to fit scurves on the early data points, and see the sorts of curves that can fit well for that.
library(tidyverse)
library(purrr)
tb <- tibble::tribble(
~ value,
2,
5,
18,
28,
43,
61,
95,
139,
245,
388,
593,
978,
1501,
2336,
2922,
3513,
4747,
5823,
6566,
7161,
8042,
9000,
10075,
11364,
12729,
13938,
14991,
16169
) %>% mutate(
rownum = row_number()
)
opt_func <- function(param_to_opt) {
tb2 <- mutate(tb,
value2 = value / (param_to_opt * max(value))
)
model <- glm(value2 ~ rownum, family = binomial(link = "logit"),weights=log(tb2$rownum), data = tb2)
return( sqrt(mean(model$residuals^2)))
}
ser <- 1:1000 * 10000
rmse <- map_dbl(ser , ~opt_func(.))
min_index <- which(rmse==min(rmse))
ser[[min_index]]
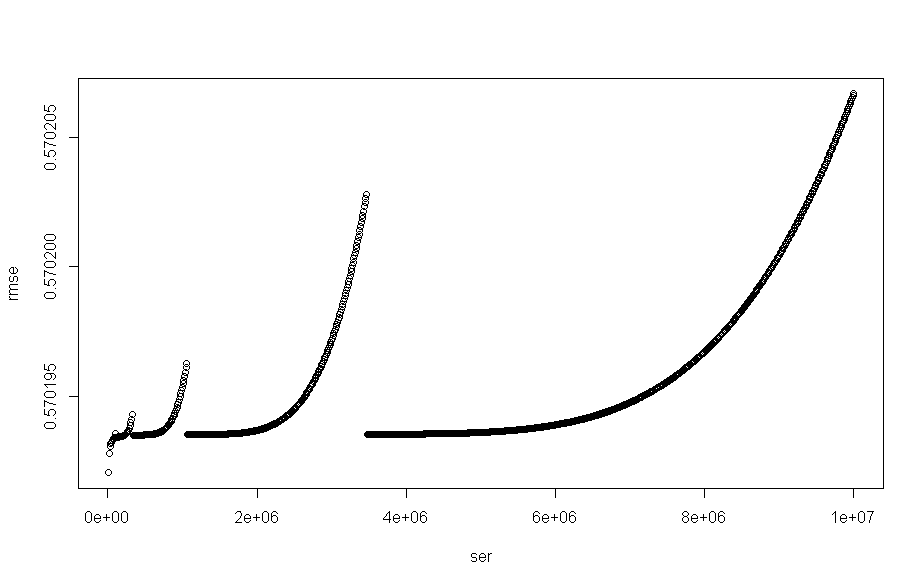
plot(x = ser,y=rmse)
rmse[rmse> 0.570192 -0.000001 & rmse <0.570192 +0.000001]
#only 2 values
rmse[rmse> 0.570192 -0.000002 & rmse <0.570192 +0.000002]
#477 values
rmse[rmse> 0.570192 -0.0000015 & rmse <0.570192 +0.0000015]
#43 values ' so will plot 43 'most likey' s curves from the 1000 trialled.
parms_to_plot <- which(rmse> 0.570192 -0.0000015 & rmse <0.570192 +0.0000015)
extrude_length <- 150
new_prediction <- function(chosen_parm)
{
tb2 <- mutate(tb,
rownum = row_number(),
value2 = value / (chosen_parm * max(value))
)
model <- glm(value2 ~ rownum, family = binomial(link = "logit"),weights = log(tb2$rownum), data = tb2)
mtr <- max(tb2$rownum) + 1
tb2_extended <- union_all(tb2,
data.frame(value=rep(NA_real_,extrude_length),
rownum=mtr:(mtr+extrude_length -1),
value2=rep(NA_real_,extrude_length)))
fitted.results <- predict(model,
newdata=tb2_extended,type='response')
tb3 <- cbind(tb2_extended,fitted.results)
tb4 <- mutate(tb3,
rescaled_prediction = fitted.results * chosen_parm *max(value,na.rm = TRUE))
select(tb4,
rescaled_prediction)
}
extruded_plots <- map_dfc(ser[parms_to_plot],
~new_prediction(.))
mtr <- max(tb$rownum) + 1
tb2_extended <- union_all(tb,
data.frame(value=rep(NA_real_,extrude_length),
rownum=mtr:(mtr+extrude_length -1)))
data_to_plot<-bind_cols(tb2_extended,extruded_plots)
library(plotly)
p<- plot_ly(data=data_to_plot,
type="scatter",
mode="lines",
x=~rownum,
y=~value,
line= list(
color="#0000FFFF"))
additional_line_names <- setdiff(names(data_to_plot),
c("value","rownum"))
add_next_trace <- function(name)
{
p<<-p %>% add_trace(y=as.formula(paste0("~",name)),
line= list(
color="#FF000044",
dash = 'dash')
)
}
walk(additional_line_names,
add_next_trace
)
p_close <- p %>% layout(xaxis = list(range = c(1, 40)),
yaxis = list(range = c(0,60000)))
pfull <- p
in the above i have plot() of the root mean square error , rmse that looks like
I then try to find some number of values that are towards the minima of that.
I settle on bounds which represent the 43 smallest values.
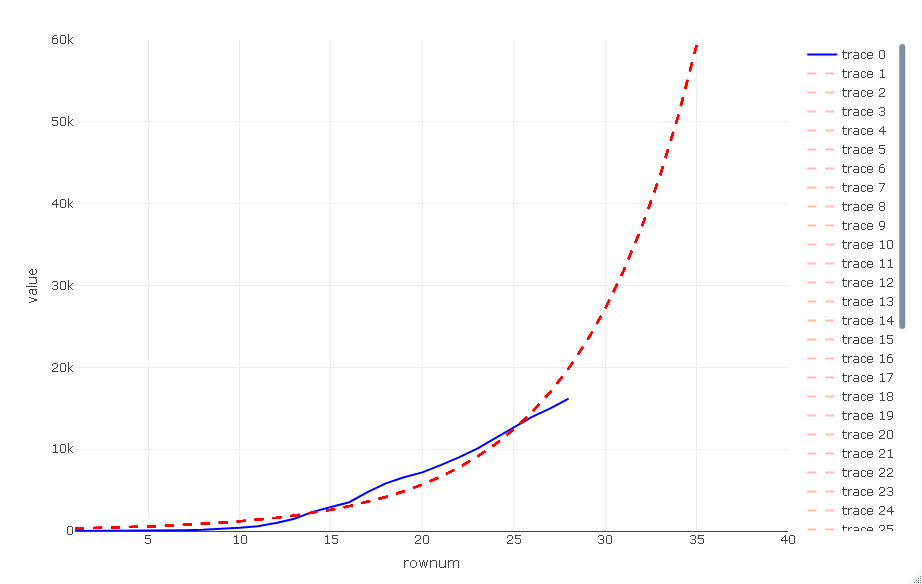
and I plot them.
there is a zoomed in view
p_close
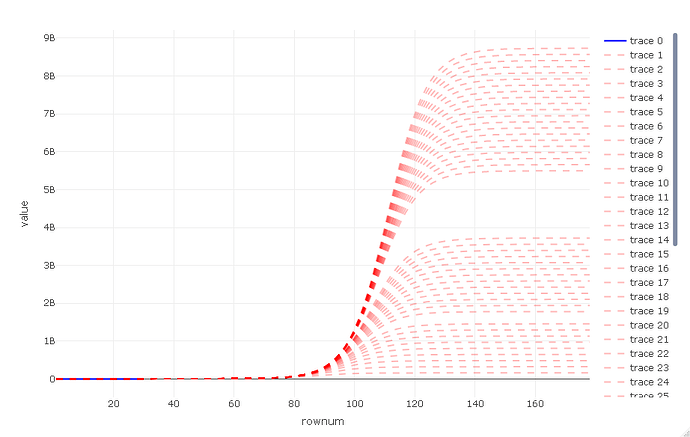
and a zoomed out view
p_full
As can be seen here, there is a range from about 2% of earth population to over 100% , worrying :-/
I wouldn't trust these results to give any insight... but it was interesting to think about abstractly.