help with categorical regression

General
1

Hi, I am currently trying to run a linear regression on a dataset relating to pedestrian behavior, however all of my variables are categorical! I have used the ifelse function to isolate levels of these variables which I 'think' has worked. I was wondering if someone with a bit more knowledge could give me some guidance.

My 'Signal' variable is divided into 4 levels and 'Sex' is divided into male and female so this is what I did:

both_red <- ifelse(cleaned_data_3$Signal == 'R/R', 1,0)
red_green <- ifelse(cleaned_data_3$Signal == 'R/G', 1,0)
green_red <- ifelse(cleaned_data_3$Signal == 'G/R', 1,0)
male <- ifelse(cleaned_data_3$Sex == 'Male',1,0)
df <- data.frame(male3 = male3,
both_red = both_red,
red_green = red_green)
model_Hyp1 <- lm(formula = both_red + red_green ~ male, data = df)
summary(model_Hyp1)

I was testing the hypothesis that males are more likely to initiate a road crossing on the red signal, have I done this linear regression correctly?

2

The syntax is fine, but the choice of model isn't.

lm relies on the response variable being able to take continuous values. When the response variable is binary (here, lights are in the both_red or the red_green state), logistic regression with the glm() function is indicated, but not if all variables are discrete, in which case the default family argument must be replaced with poisson(link = "log").

But the problem you've chosen is only whether there is an association between road crossing on the red signal (1/0) and assignment to male gender (1/0).

library(BayesFactor)
#> Loading required package: coda
#> Loading required package: Matrix
#> ************
#> Welcome to BayesFactor 0.9.12-4.4. If you have questions, please contact Richard Morey (richarddmorey@gmail.com).
#> 
#> Type BFManual() to open the manual.
#> ************
library(DescTools)
library(lsr)
data("PhdPubs", package = "vcdExtra")
# pretend it's the crossing data
pedxing <- PhdPubs[2:3]
colnames(pedxing) <- c("jwalk","male")
pedxing$jwalk <- as.factor(pedxing$jwalk)
pedxing$male <- as.factor(pedxing$male)
head(pedxing)
#>   jwalk male
#> 1     0    1
#> 2     1    0
#> 3     1    0
#> 4     0    1
#> 5     1    0
#> 6     1    1
(tab <- table(pedxing))
#>      male
#> jwalk   0   1
#>     0 113 381
#>     1 196 225
GTest(table(tab))
#> 
#>  Log likelihood ratio (G-test) goodness of fit test
#> 
#> data:  table(tab)
#> G = 0, X-squared df = 3, p-value = 1
Assocs(tab)
#>                        estimate  lwr.ci  upr.ci
#> Contingency Coeff.       0.2421       -       -
#> Cramer V                 0.2496  0.1848  0.3144
#> Kendall Tau-b           -0.2496 -0.3128 -0.1863
#> Goodman Kruskal Gamma   -0.4920 -0.5997 -0.3843
#> Stuart Tau-c            -0.2353 -0.2953 -0.1753
#> Somers D C|R            -0.2368 -0.2972 -0.1765
#> Somers D R|C            -0.2630 -0.3319 -0.1941
#> Pearson Correlation     -0.2496 -0.3094 -0.1878
#> Spearman Correlation    -0.2496 -0.3094 -0.1878
#> Lambda C|R               0.0000  0.0000  0.0000
#> Lambda R|C               0.1971  0.1238  0.2705
#> Lambda sym               0.1137  0.0704  0.1570
#> Uncertainty Coeff. C|R   0.0490  0.0241  0.0739
#> Uncertainty Coeff. R|C   0.0454  0.0223  0.0686
#> Uncertainty Coeff. sym   0.0471  0.0232  0.0711
#> Mutual Information       0.0452       -       -
crosstab <- xtabs(~ jwalk + male, pedxing)
PlotMosaic(crosstab)


associationTest(~jwalk + male, pedxing)
#> 
#>      Chi-square test of categorical association
#> 
#> Variables:   jwalk, male 
#> 
#> Hypotheses: 
#>    null:        variables are independent of one another
#>    alternative: some contingency exists between variables
#> 
#> Observed contingency table:
#>      male
#> jwalk   0   1
#>     0 113 381
#>     1 196 225
#> 
#> Expected contingency table under the null hypothesis:
#>      male
#> jwalk   0   1
#>     0 167 327
#>     1 142 279
#> 
#> Test results: 
#>    X-squared statistic:  55.938 
#>    degrees of freedom:  1 
#>    p-value:  <.001 
#> 
#> Other information: 
#>    estimated effect size (Cramer's v):  0.247 
#>    Yates' continuity correction has been applied
contingencyTableBF(crosstab, sampleType = "jointMulti")
#> Bayes factor analysis
#> --------------
#> [1] Non-indep. (a=1) : 311517421789 ±0%
#> 
#> Against denominator:
#>   Null, independence, a = 1 
#> ---
#> Bayes factor type: BFcontingencyTable, joint multinomial
contingencyTableBF(crosstab, sampleType = "poisson")
#> Bayes factor analysis
#> --------------
#> [1] Non-indep. (a=1) : 414904596594 ±0%
#> 
#> Against denominator:
#>   Null, independence, a = 1 
#> ---
#> Bayes factor type: BFcontingencyTable, poisson
contingencyTableBF(crosstab, sampleType = "indepMulti", fixedMargin="rows")
#> Bayes factor analysis
#> --------------
#> [1] Non-indep. (a=1) : 209230723321 ±0%
#> 
#> Against denominator:
#>   Null, independence, a = 1 
#> ---
#> Bayes factor type: BFcontingencyTable, independent multinomial
contingencyTableBF(crosstab, sampleType = "hypergeom")
#> Bayes factor analysis
#> --------------
#> [1] Non-indep. (a=1) : 153916769244 ±0%
#> 
#> Against denominator:
#>   Null, independence, a = 1 
#> ---
#> Bayes factor type: BFcontingencyTable, hypergeometric

Created on 2023-04-07 with reprex v2.0.2

Under each these tests, the null hypothesis is that the variables are independent, and the alternative hypothesis is that they are not. Under each of the tests, we fail to accept the NULL, which is evidence for the alternative. That is, if the data represented what they purport to represent, there is strong evidence of an association between crossing against the light and malehood.

To go beyond this more is needed. For example, data be required to answer the question

At a randomly selected street crossing what is the probability of observing a male crossing on the red signal?

might require data on how many intersections, how many have signals, how signal cycles per day, how many pedestrian males and what is the distribution of crossings per signal cycle over the course of the observation period.

2 Likes
3

I appreciate the reply! In the entire dataset, I have the variables: age (3 levels), signal type (4 levels), gender (2 levels), following (2 levels), hesitation (2 levels), phone distraction (2 levels), and music distraction (2 levels). I'm trying to use a statistical test and was advised to use either a linear or logistical regression. I have a variety of different hypotheses relating to different levels of each variable i.e. use of mobile phone and headphones = greater chance of crossing red signal due to distraction. I'm a little stumped as to how to appropriately test these and whether the approach I took was correct.

4

Let me gently disagree with @technocrat here. (Boy, that doesn't happen very often.)

@technocrat's suggestion to use a logistic regression is a good idea, but there's nothing necessarily wrong with using a linear regression when the dependent variable has only two values. This is what is called a linear probability model. Here is one reference, https://www.econometrics-with-r.org/11-1-binary-dependent-variables-and-the-linear-probability-model.html.

The advantage of the linear probability model is that it is easier to interpret, although there are also some disadvantages. My recommendation would be to go with @technocrat's suggestion, but the linear regression is not "wrong."

2 Likes
6

So with my hypotheses varying in specific levels, in terms of a report would it be normal to breakdown my collected results and analyse them on an individual hypothesis basis rather than assessing the interaction between all variables on each other??

7

@technocrat i attempted the poisson model but i kept getting further errors. I thought I'd provide a bit more detail.

This is my dataset, but ignore the traffic density and children column as they are of no use.

Sex Age Phone Music Children FamAll CrowdAll Following Signal Traffic Hesitation
0 Elderly 1 1 0 0 1 0 R/R Low 1
0 Elderly 0 1 0 0 1 1 R/R Low 0
0 Elderly 1 0 0 0 0 1 G/G Low 1
0 Elderly 0 0 0 0 0 1 G/G Medium 0
0 Middle 1 1 0 0 3 1 R/R Medium 0
0 Middle 1 1 0 0 4 0 R/R Medium 0
0 Middle 0 0 0 1 5 0 G/G Medium 1
0 Middle 1 0 0 0 1 0 R/R Medium 0
0 Middle 0 0 0 1 1 0 R/R Low 0
0 Middle 0 1 0 0 1 1 R/R Low 1
0 Middle 0 0 0 0 0 1 R/R Low 0
0 Middle 1 0 0 0 1 0 G/G Medium 0
0 Middle 1 0 0 1 2 0 R/G High 0
0 Middle 0 0 0 1 0 1 R/R Low 0
0 Middle 0 1 0 0 1 1 R/R Medium 0
0 Middle 0 1 0 0 2 0 G/G Medium 1
0 Middle 1 1 0 0 3 0 R/R Medium 0
0 Middle 0 0 0 1 1 1 R/R Medium 0
0 Middle 0 0 0 1 0 0 G/G Medium 1
0 Middle 1 0 0 0 0 1 G/G Low 1
0 Middle 0 0 0 2 1 0 G/R Low 0
0 Middle 1 0 0 0 13 0 G/G Low 0
0 Middle 0 0 0 2 0 1 R/R Medium 0
0 Middle 0 0 0 1 1 0 G/G Low 0
0 Middle 0 1 0 0 1 0 R/G Medium 1
0 Middle 0 0 0 0 1 1 R/R Low 0
0 Middle 0 1 0 1 0 0 R/R Medium 1
0 Middle 0 1 0 0 1 1 R/R Low 0
0 Youth 1 0 0 0 1 0 G/R Medium 0
0 Youth 0 0 0 1 1 0 G/G Low 0
0 Youth 0 0 0 0 1 1 G/G Low 0
0 Youth 0 1 0 0 2 0 R/R Low 1
0 Youth 1 0 1 0 1 1 G/G Low 0
0 Youth 1 1 0 1 0 1 G/G Low 0
0 Youth 1 0 0 0 0 0 G/G Low 0
0 Youth 1 0 0 1 1 G/G Medium 0
0 Youth 0 0 1 0 1 0 G/G Low 1
0 Youth 0 1 0 0 0 1 G/G Low 1
0 Youth 1 0 0 0 1 1 R/R None 0
0 Youth 0 0 0 0 0 1 G/G Low 0
0 Youth 1 1 0 0 1 0 G/R Low 1
0 Youth 0 1 0 0 3 0 G/G Low 1
0 Youth 1 0 0 0 3 0 R/G Medium 0
0 Youth 0 0 1 1 0 0 G/G Medium 0
0 Youth 0 1 0 0 2 1 R/R Medium 0
0 Youth 0 0 0 0 1 0 R/G Low 0
0 Youth 1 0 0 1 0 0 G/G Low 0
0 Youth 1 0 0 0 1 0 R/R Medium 1
0 Youth 1 0 0 0 2 0 R/R Medium 1
0 Youth 0 1 0 0 0 0 G/G High 1
0 Youth 0 0 0 1 0 1 G/G Medium 0
0 Youth 0 0 0 1 1 0 G/G High 0
0 Youth 0 1 0 0 1 0 G/G Medium 1
0 Youth 1 0 0 0 1 0 G/G Medium 1
0 Youth 0 0 0 1 0 1 R/R Medium 0
0 Youth 0 1 0 0 1 1 R/R Medium 0
0 Youth 0 1 0 0 0 0 G/G Low 0
0 Youth 0 0 0 3 0 1 G/G Medium 0
0 Youth 1 0 0 1 0 0 G/G Medium 0
0 Youth 0 0 0 0 0 0 G/G Medium 1
0 Youth 0 0 1 0 1 1 R/R Medium 0
0 Youth 0 0 0 1 0 0 G/G Medium 0
1 Elderly 0 0 0 0 0 1 R/R Low 0
1 Elderly 0 1 0 0 2 1 G/G Medium 0
1 Elderly 1 0 0 0 1 0 G/G Low 1
1 Elderly 1 0 0 0 0 0 G/R Medium 0
1 Elderly 0 0 0 0 2 0 G/R Medium 0
1 Elderly 1 1 0 0 4 0 G/G Medium 1
1 Elderly 1 1 0 1 4 1 R/R Medium 0
1 Elderly 1 1 0 0 0 1 G/G None 0
1 Middle 0 0 0 0 2 0 R/R Medium 0
1 Middle 0 0 0 0 2 0 R/R Medium 1
1 Middle 0 1 0 0 1 1 G/G Medium 0
1 Middle 0 0 0 0 6 1 R/R Medium 0
1 Middle 0 0 0 1 3 0 R/R Medium 1
1 Middle 0 0 0 1 1 0 R/R Low 0
1 Middle 1 0 0 0 1 1 R/G Medium 1
1 Middle 1 0 0 1 1 0 R/G Low 0
1 Middle 1 0 0 0 1 0 R/R Low 0
1 Middle 0 0 0 0 0 0 R/R Medium 0
1 Middle 0 0 0 1 1 1 R/R Medium 0
1 Middle 0 0 0 0 0 1 R/G Low 1
1 Middle 0 0 0 1 1 0 R/R Low 0
1 Middle 1 0 0 0 1 0 R/R Medium 0
1 Middle 0 1 0 0 1 1 G/G Low 0
1 Middle 0 0 0 0 1 0 G/G Medium 1
1 Middle 0 1 0 0 1 1 G/R Medium 0
1 Middle 1 0 0 1 0 0 R/R Medium 0
1 Middle 0 0 0 0 1 1 R/R Low 1
1 Middle 0 0 0 1 2 1 R/R Medium 0
1 Middle 0 0 0 2 0 0 R/R Low 0
1 Middle 1 1 0 0 2 0 R/R Medium 0
1 Middle 1 1 0 0 2 0 G/G Low 0
1 Middle 0 0 0 0 2 0 G/G Medium 0
1 Middle 0 1 0 0 3 1 R/G Medium 0
1 Middle 0 0 1 0 0 1 G/G Low 0
1 Middle 1 0 0 0 1 0 G/G Medium 1
1 Middle 0 1 0 0 3 1 R/R Medium 0
1 Middle 0 1 0 2 1 0 G/G Low 1
1 Middle 0 0 0 1 3 1 G/G Medium 1
1 Middle 0 1 0 0 1 0 R/R Medium 1
1 Middle 1 1 0 0 1 1 R/R High 0
1 Youth 0 1 0 0 3 0 R/R Medium 0
1 Youth 1 0 0 0 0 1 R/R High 0
1 Youth 0 1 0 0 1 1 R/G Low 0
1 Youth 0 1 0 0 1 1 R/R Medium 1
1 Youth 0 1 0 0 1 1 G/G Medium 0
1 Youth 1 0 0 1 0 0 G/R Medium 1
1 Youth 0 0 0 1 0 1 G/G Low 0
1 Youth 1 0 0 4 2 0 R/R Low 0
1 Youth 1 1 0 0 1 0 R/G Low 0
1 Youth 0 1 0 0 1 1 G/G Low 1
1 Youth 0 0 0 1 1 0 R/R Low 1
1 Youth 0 1 0 0 1 1 G/G Low 0
1 Youth 1 1 0 0 2 1 G/G Low 0
1 Youth 0 1 0 0 1 0 R/G Low 1
1 Youth 0 0 0 1 0 1 R/R Medium 0
1 Youth 1 0 0 0 1 0 G/G Low 0
1 Youth 0 1 0 0 0 1 R/R None 0
1 Youth 0 1 0 0 1 1 R/R Medium 0
1 Youth 1 1 0 0 0 1 R/R Medium 0
1 Youth 0 0 0 0 3 0 G/R Medium 1
1 Youth 1 1 0 0 3 1 R/R High 0
1 Youth 1 1 0 0 1 1 R/R Medium 1
1 Youth 1 0 0 0 2 0 G/G Medium 0
1 Youth 0 1 0 0 1 1 R/G Medium 0
1 Youth 0 1 0 0 1 1 G/G Medium 1
1 Youth 0 1 0 0 1 1 R/R Medium 0
1 Youth 1 0 0 0 0 1 R/G Medium 0
1 Youth 0 0 0 1 1 0 R/G Medium 0
1 Youth 0 0 0 0 1 0 R/G Medium 0
1 Youth 0 0 0 0 3 0 G/R Low 1
1 Youth 0 0 0 0 4 1 R/R Medium 1
1 Youth 0 1 0 0 2 0 G/G Medium 1
1 Youth 1 0 0 1 1 1 R/G Medium 0
1 Youth 0 1 0 0 1 0 R/G High 0
1 Youth 0 0 0 0 1 0 G/G Medium 0
1 Youth 0 0 0 0 0 1 R/R Medium 0
1 Youth 0 0 0 0 0 1 R/R Low 0
1 Youth 0 1 0 0 1 1 R/R Medium 1
1 Youth 0 1 0 0 1 1 G/G Medium 0
1 Youth 0 0 0 0 1 1 R/R Low 0

The hypotheses and corresponding script are:

  • Youth and middle aged more likely to cross while interacting with music and/or mobile phones

middle <- ifelse(cleaned_data_3$Age == 'Middle', 1,0)

df <- data.frame(Phone = Phone,
music = music,
youth = youth,
middle = middle)
model_Hyp7 <- glm(Phone + Music ~ middle + youth)
summary(model_Hyp7)

  • Individuals using mobile phones and/or music more likely to cross on and/or end at red light

df <- data.frame(Phone = Phone,
both_red = both_red,
green_red = green_red,
Music = Music)
model_Hyp6 <- lm(both_red + green_red ~ Phone + Music)
summary(model_Hyp6)

  • Individuals more likely to cross on red light if crowd size is 0

crowdAll <- cleaned_data_4$CrowdAll
df3 <- data.frame(crowdAll == crowdAll)
model_Hyp5 <- lm(both_red ~ crowdAll, data = df3)
summary(model_Hyp5)

  • females more likely to hesitate and wait for green light

female <- ifelse(cleaned_data_4$Sex =='Female', 1,0)
both_green <- ifelse(cleaned_data_4$Signal == 'G/G', 1,0)
df2 <- data.frame(female = female,
both_green = both_green,
red_green = red_green,
green_red = green_red)
model_Hyp4 <- lm(both_green ~ female, data = df2)
summary(model_Hyp4)

  • Compliance will be observed when risk taking behaviours take place during red light

follow <- ifelse(cleaned_data_3$Following == 'Followed', 1,0)
df <- data.frame(follow = follow,
both_red = both_red)

model_Hyp33 <- lm(follow ~ both_red, data = df)
summary(model_Hyp33)

  • Younger citizens more likely to hesitate and wait for red light

df <- data.frame (both_red = both_red,
hesitation = hesitation,
youth)
youth <- ifelse (cleaned_data_4$Age == 'Youth', 1,0)
hesitation <- ifelse (cleaned_data_4$Hesitation == 'Yes', 1,0)

model_Hyp22 <- lm(both_red + hesitation ~ youth, data = df)
summary(model_Hyp22)

  • Males more likely to take risk and cross on red light

both_red <- ifelse(cleaned_data_4$Signal == 'R/R', 1,0)
red_green <- ifelse(cleaned_data_4$Signal == 'R/G', 1,0)
green_red <- ifelse(cleaned_data_4$Signal == 'G/R', 1,0)
male <- ifelse(cleaned_data_4$Sex == '1',1,0)
df <- data.frame(male = male,
both_red = both_red,
red_green = red_green,
green_red = green_red)
model_Hyp1 <- lm(formula = both_red + red_green ~ male, data = df)
summary(model_Hyp1)

If you did get this far then thank you. I am almost certain the way I've gone about this is probably incorrect and convoluted so any guidance and advice are more than appreciated.

2 Likes
8

Since you made it nice and easy I ran the last estimate you posted, getting.

Call:
lm(formula = both_red + red_green ~ male, data = df)

Residuals:
    Min      1Q  Median      3Q     Max 
-0.6250 -0.4516  0.3750  0.3750  0.5484 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  0.45161    0.06268   7.205 3.29e-11 ***
male         0.17339    0.08351   2.076   0.0397 *  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.4936 on 140 degrees of freedom
Multiple R-squared:  0.02987,	Adjusted R-squared:  0.02294 
F-statistic: 4.311 on 1 and 140 DF,  p-value: 0.0397

The interpretation is that women have a 45 percent probability of crossing on red and that men have a 62 percent probability. And the difference is statistically significant at the usual levels.

But I suspect you knew that and that I'm missing your question.

1 Like
9

Cheers for the response! I was more asking if the formulas I made from the dataset for each of the hypotheses was done correctly. I’m essentially seeking advice from people more experienced in the field for either a bit of reassurance or advice if i’d done it wrong!

10

Looks good to me!

(Arguably, you should be calculating heteroskedasticity robust standard errors. May or may not be worth the effort depending on your use. It won't affect the estimated effects.)

11

It’s a final research project for a bachelors in psychology. Not going to lie that word could be a made up for all I’m aware!

12

I'm not in psychology, but I'd say you're doing pretty good!

If you want to get fancier (which you may not), you could do something like

lm(formula = both_red + red_green ~ male+crowdAll +male*crowdAll  , data = df)

To see if there is a difference between men's and women's response when there is a crowd.

13

Wolfgang Pauli (he of the Pauli Exclusion Principle) had a trenchant quote that applies

Das is nicht einmal falsch.

that I have to invoke. (The slam is against the idea, not @startz.) Not even the proponents of linear probability regression apply it to binary on binary situations.

14

This is a good discussion to continue @startz (my fellow Richard) because I've revisited the linear probability model (PLM). I first saw it a few years ago in an econometric's paper on gender discrimination in the financial industry and was not convinced by the authors' defense of the methodology.

The first example given in the cited text is one in which I had a lot of domain knowledge before 2009, so it serves as a good motivating example. The data to be analyzed concerns mortgage loan application approvals.

--------------------------------------------------------- 
Describe HMDA (data.frame):

data frame:	2380 obs. of  14 variables
		2380 complete cases (100.0%)

  Nr  ColName    Class    NAs  Levels                 
  1   deny       factor   .    (2): 1-no, 2-yes       
  2   pirat      numeric  .                           
  3   hirat      numeric  .                           
  4   lvrat      numeric  .                           
  5   chist      factor   .    (6): 1-1, 2-2, 3-3,    
                               4-4, 5-5, ...          
  6   mhist      factor   .    (4): 1-1, 2-2, 3-3, 4-4
  7   phist      factor   .    (2): 1-no, 2-yes       
  8   unemp      numeric  .                           
  9   selfemp    factor   .    (2): 1-no, 2-yes       
  10  insurance  factor   .    (2): 1-no, 2-yes       
  11  condomin   factor   .    (2): 1-no, 2-yes       
  12  afam       factor   .    (2): 1-no, 2-yes       
  13  single     factor   .    (2): 1-no, 2-yes       
  14  hschool    factor   .    (2): 1-no, 2-yes

The response (dependent) variable (or regressand) Y is deny, so a value of 0 indicates loan approval (deny is FALSE, 0) while a value of 1 is disapproval.

The treatment (independent) variable (or regressor) X is pirat called P/I ratio, the ratio of scheduled payments of principal and interest on the mortgage loan to income.

The PLM model claims that Y = \beta_0 + \beta_1 * X - u where

\beta_0 is the y-intercept of the regression line
\beta_1 is the slope of the regression line
u is an error term

Earlier in the text, u is explained

the error term u\dots captures additional random effects \dots all the differences between the regression line and the actual observed data. Beside pure randomness, these deviations could also arise from measurement errors or, as will be discussed later, could be the consequence of leaving out other factors that are relevant in explaining the dependent variable.

u, accordingly, may as well stand for Universal Fudge Factor

u is not a term considered necessary in ordinary least square regression, and for good reason. If the question that a linear regression is supposed to answer is what is the probability of observing Y in the presence of X and the answer is 2.54 + 1.39x, plus or minus some other stuff, that is not a very satisfactory state of affairs.

Let's start by ticking off one other consideration. The formula is linear in its parameters, not Y = \beta_0 + \beta_1x^2 + u.

So, here's the example adapted from the text:

library(ggplot2)

data("HMDA",package = "AER")
# inspect the data
DescTools::Desc(HMDA, plotit = TRUE)
#> ------------------------------------------------------------------------------ 
#> Describe HMDA (data.frame):
#> 
#> data frame:  2380 obs. of  14 variables
#>      2380 complete cases (100.0%)
#> 
#>   Nr  ColName    Class    NAs  Levels                           
#>   1   deny       factor   .    (2): 1-no, 2-yes                 
#>   2   pirat      numeric  .                                     
#>   3   hirat      numeric  .                                     
#>   4   lvrat      numeric  .                                     
#>   5   chist      factor   .    (6): 1-1, 2-2, 3-3, 4-4, 5-5, ...
#>   6   mhist      factor   .    (4): 1-1, 2-2, 3-3, 4-4          
#>   7   phist      factor   .    (2): 1-no, 2-yes                 
#>   8   unemp      numeric  .                                     
#>   9   selfemp    factor   .    (2): 1-no, 2-yes                 
#>   10  insurance  factor   .    (2): 1-no, 2-yes                 
#>   11  condomin   factor   .    (2): 1-no, 2-yes                 
#>   12  afam       factor   .    (2): 1-no, 2-yes                 
#>   13  single     factor   .    (2): 1-no, 2-yes                 
#>   14  hschool    factor   .    (2): 1-no, 2-yes                 
#> 
#> 
#> ------------------------------------------------------------------------------ 
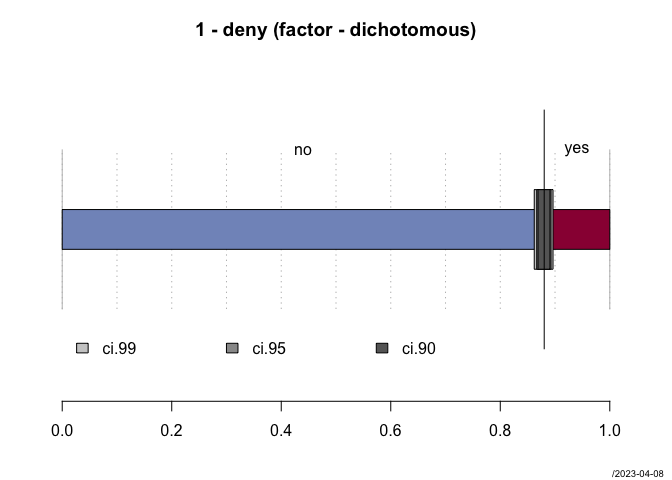
#> 1 - deny (factor - dichotomous)
#> 
#>   length      n    NAs unique
#>    2'380  2'380      0      2
#>          100.0%   0.0%       
#> 
#>       freq   perc  lci.95  uci.95'
#> no   2'095  88.0%   86.7%   89.3%
#> yes    285  12.0%   10.7%   13.3%
#> 
#> ' 95%-CI (Wilson)


#> ------------------------------------------------------------------------------ 
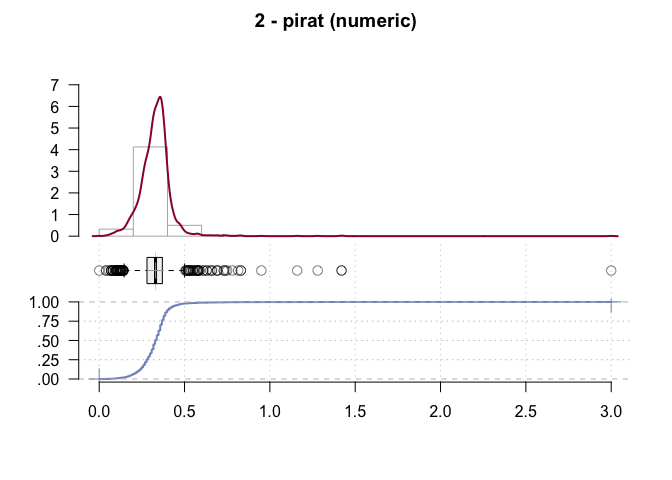
#> 2 - pirat (numeric)
#> 
#>   length       n     NAs  unique      0s    mean    meanCI'
#>    2'380   2'380       0     519       1  0.3308    0.3265
#>           100.0%    0.0%            0.0%            0.3351
#>                                                           
#>      .05     .10     .25  median     .75     .90       .95
#>   0.1900  0.2300  0.2800  0.3300  0.3700  0.4100    0.4401
#>                                                           
#>    range      sd   vcoef     mad     IQR    skew      kurt
#>   3.0000  0.1073  0.3242  0.0608  0.0900  8.0816  174.0668
#>                                                           
#> lowest : 0.0, 0.04 (2), 0.056, 0.0699, 0.07 (3)
#> highest: 0.95, 1.16, 1.28, 1.42 (2), 3.0
#> 
#> ' 95%-CI (classic)


#> ------------------------------------------------------------------------------ 
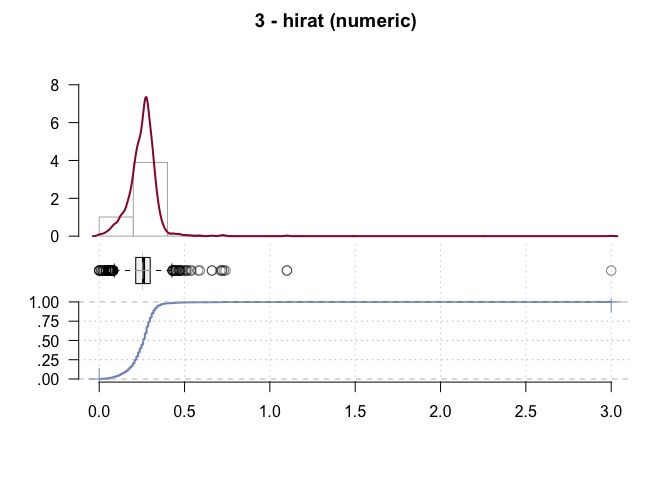
#> 3 - hirat (numeric)
#> 
#>     length         n       NAs    unique        0s       mean      meanCI'
#>      2'380     2'380         0       500         3   0.255346    0.251461
#>               100.0%      0.0%                0.1%               0.259231
#>                                                                          
#>        .05       .10       .25    median       .75        .90         .95
#>   0.120000  0.160000  0.214000  0.260000  0.298825   0.330000    0.350000
#>                                                                          
#>      range        sd     vcoef       mad       IQR       skew        kurt
#>   3.000000  0.096656  0.378528  0.059304  0.084825  10.306709  277.842289
#>                                                                          
#> lowest : 0.0 (3), 0.00085, 0.01 (2), 0.02 (3), 0.028
#> highest: 0.72 (2), 0.73, 0.74, 1.1 (2), 3.0
#> 
#> heap(?): remarkable frequency (6.0%) for the mode(s) (= 0.28)
#> 
#> ' 95%-CI (classic)


#> ------------------------------------------------------------------------------ 
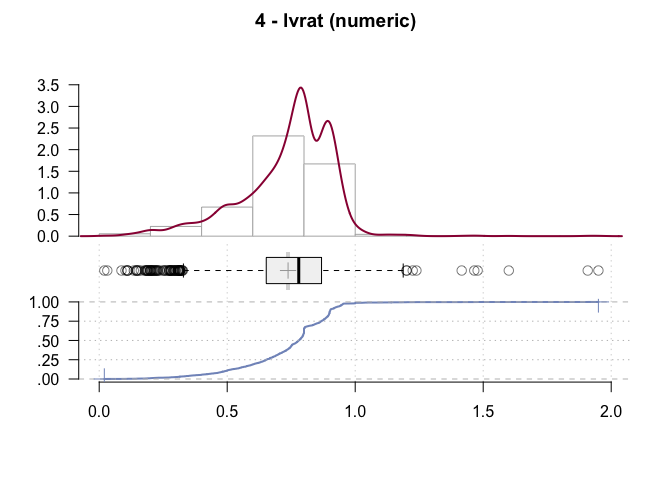
#> 4 - lvrat (numeric)
#> 
#>      length          n        NAs     unique         0s        mean     meanCI'
#>       2'380      2'380          0      1'537          0   0.7377759  0.7305909
#>                 100.0%       0.0%                  0.0%              0.7449609
#>                                                                               
#>         .05        .10        .25     median        .75         .90        .95
#>   0.3797828  0.4895612  0.6526808  0.7795364  0.8684586   0.9040000  0.9412107
#>                                                                               
#>       range         sd      vcoef        mad        IQR        skew       kurt
#>   1.9300000  0.1787510  0.2422836  0.1524358  0.2157779  -0.6013342  2.9580578
#>                                                                               
#> lowest : 0.02, 0.0315107, 0.0869565, 0.1025641, 0.1096491
#> highest: 1.4651163, 1.4782609, 1.6, 1.9083333, 1.95
#> 
#> heap(?): remarkable frequency (6.1%) for the mode(s) (= 0.8)
#> 
#> ' 95%-CI (classic)


#> ------------------------------------------------------------------------------ 
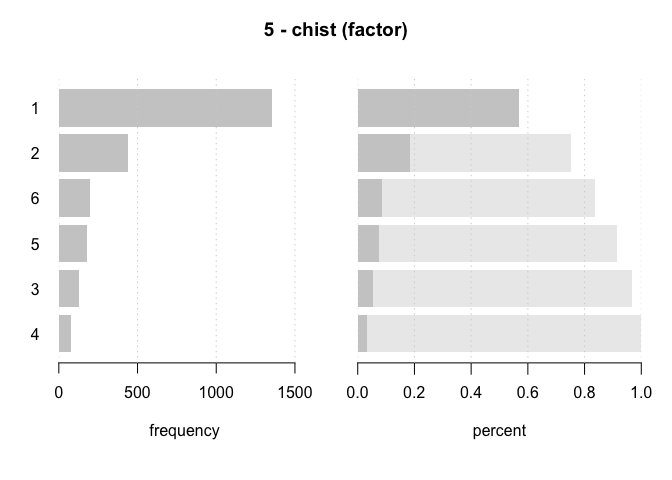
#> 5 - chist (factor)
#> 
#>   length      n    NAs unique levels  dupes
#>    2'380  2'380      0      6      6      y
#>          100.0%   0.0%                     
#> 
#>    level   freq   perc  cumfreq  cumperc
#> 1      1  1'353  56.8%    1'353    56.8%
#> 2      2    441  18.5%    1'794    75.4%
#> 3      6    201   8.4%    1'995    83.8%
#> 4      5    182   7.6%    2'177    91.5%
#> 5      3    126   5.3%    2'303    96.8%
#> 6      4     77   3.2%    2'380   100.0%


#> ------------------------------------------------------------------------------ 
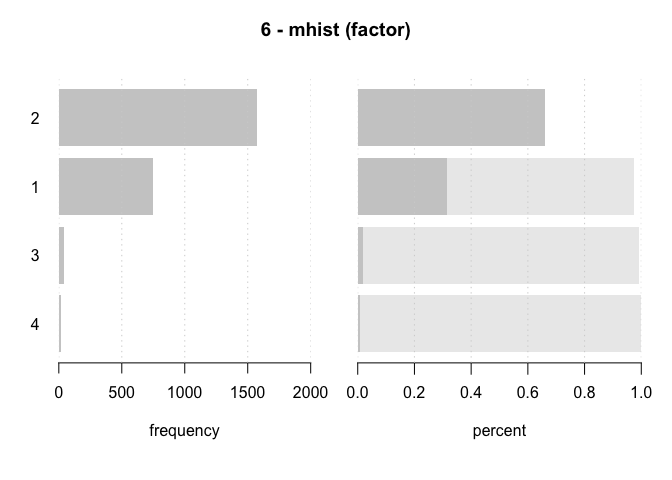
#> 6 - mhist (factor)
#> 
#>   length      n    NAs unique levels  dupes
#>    2'380  2'380      0      4      4      y
#>          100.0%   0.0%                     
#> 
#>    level   freq   perc  cumfreq  cumperc
#> 1      2  1'571  66.0%    1'571    66.0%
#> 2      1    747  31.4%    2'318    97.4%
#> 3      3     41   1.7%    2'359    99.1%
#> 4      4     21   0.9%    2'380   100.0%


#> ------------------------------------------------------------------------------ 
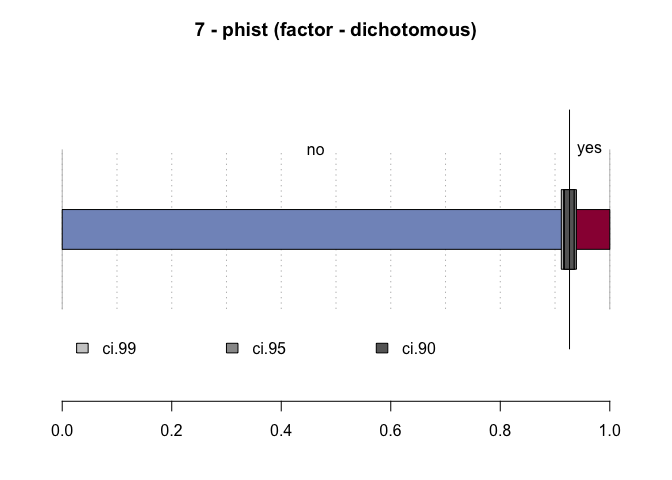
#> 7 - phist (factor - dichotomous)
#> 
#>   length      n    NAs unique
#>    2'380  2'380      0      2
#>          100.0%   0.0%       
#> 
#>       freq   perc  lci.95  uci.95'
#> no   2'205  92.6%   91.5%   93.6%
#> yes    175   7.4%    6.4%    8.5%
#> 
#> ' 95%-CI (Wilson)


#> ------------------------------------------------------------------------------ 
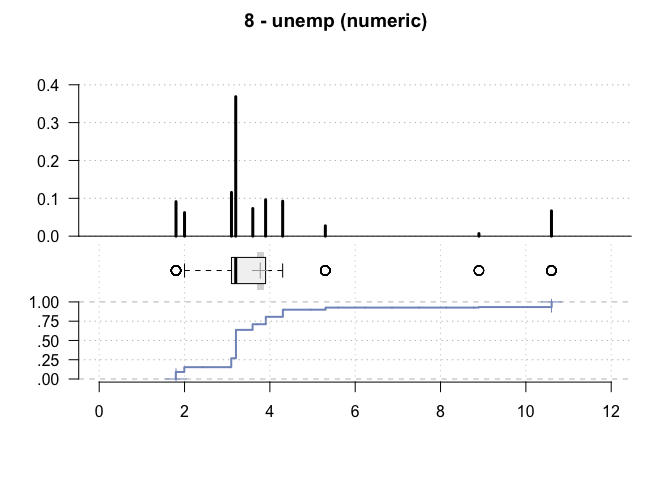
#> 8 - unemp (numeric)
#> 
#>   length       n    NAs  unique    0s  mean  meanCI'
#>    2'380   2'380      0      10     0  3.77    3.69
#>           100.0%   0.0%          0.0%          3.86
#>                                                    
#>      .05     .10    .25  median   .75   .90     .95
#>     1.80    2.00   3.10    3.20  3.90  5.30   10.60
#>                                                    
#>    range      sd  vcoef     mad   IQR  skew    kurt
#>     8.80    2.03   0.54    0.59  0.80  2.53    5.99
#>                                                    
#> 
#>                value  freq   perc  cumfreq  cumperc
#> 1   1.79999995231628   217   9.1%      217     9.1%
#> 2                  2   148   6.2%      365    15.3%
#> 3   3.09999990463257   275  11.6%      640    26.9%
#> 4   3.20000004768372   877  36.8%    1'517    63.7%
#> 5   3.59999990463257   174   7.3%    1'691    71.1%
#> 6   3.90000009536743   229   9.6%    1'920    80.7%
#> 7   4.30000019073486   220   9.2%    2'140    89.9%
#> 8   5.30000019073486    65   2.7%    2'205    92.6%
#> 9   8.89999961853027    16   0.7%    2'221    93.3%
#> 10  10.6000003814697   159   6.7%    2'380   100.0%
#> 
#> ' 95%-CI (classic)


#> ------------------------------------------------------------------------------ 
#> 9 - selfemp (factor - dichotomous)
#> 
#>   length      n    NAs unique
#>    2'380  2'380      0      2
#>          100.0%   0.0%       
#> 
#>       freq   perc  lci.95  uci.95'
#> no   2'103  88.4%   87.0%   89.6%
#> yes    277  11.6%   10.4%   13.0%
#> 
#> ' 95%-CI (Wilson)


#> ------------------------------------------------------------------------------ 
#> 10 - insurance (factor - dichotomous)
#> 
#>   length      n    NAs unique
#>    2'380  2'380      0      2
#>          100.0%   0.0%       
#> 
#>       freq   perc  lci.95  uci.95'
#> no   2'332  98.0%   97.3%   98.5%
#> yes     48   2.0%    1.5%    2.7%
#> 
#> ' 95%-CI (Wilson)


#> ------------------------------------------------------------------------------ 
#> 11 - condomin (factor - dichotomous)
#> 
#>   length      n    NAs unique
#>    2'380  2'380      0      2
#>          100.0%   0.0%       
#> 
#>       freq   perc  lci.95  uci.95'
#> no   1'694  71.2%   69.3%   73.0%
#> yes    686  28.8%   27.0%   30.7%
#> 
#> ' 95%-CI (Wilson)


#> ------------------------------------------------------------------------------ 
#> 12 - afam (factor - dichotomous)
#> 
#>   length      n    NAs unique
#>    2'380  2'380      0      2
#>          100.0%   0.0%       
#> 
#>       freq   perc  lci.95  uci.95'
#> no   2'041  85.8%   84.3%   87.1%
#> yes    339  14.2%   12.9%   15.7%
#> 
#> ' 95%-CI (Wilson)


#> ------------------------------------------------------------------------------ 
#> 13 - single (factor - dichotomous)
#> 
#>   length      n    NAs unique
#>    2'380  2'380      0      2
#>          100.0%   0.0%       
#> 
#>       freq   perc  lci.95  uci.95'
#> no   1'444  60.7%   58.7%   62.6%
#> yes    936  39.3%   37.4%   41.3%
#> 
#> ' 95%-CI (Wilson)


#> ------------------------------------------------------------------------------ 
#> 14 - hschool (factor - dichotomous)
#> 
#>   length      n    NAs unique
#>    2'380  2'380      0      2
#>          100.0%   0.0%       
#> 
#>       freq   perc  lci.95  uci.95'
#> no      39   1.6%    1.2%    2.2%
#> yes  2'341  98.4%   97.8%   98.8%
#> 
#> ' 95%-CI (Wilson)


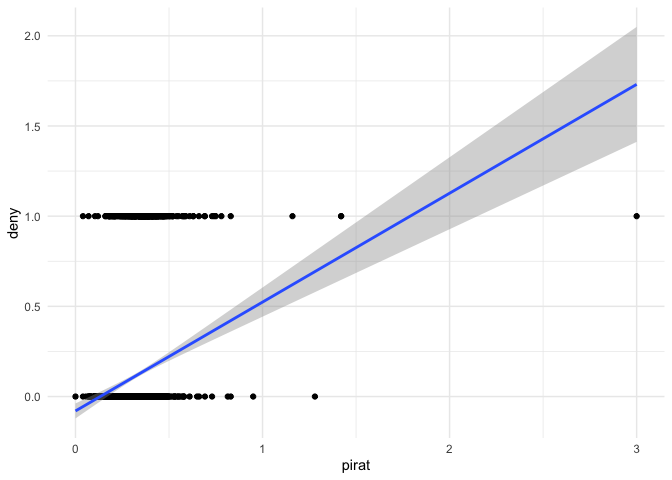
# subset the variables to be used in the example
d <- HMDA[1:2]
# convert factor to numeric 1/0
d[,1] <- as.numeric(d[,1]) - 1

# show them
d |> ggplot(aes(pirat,deny)) + 
  geom_point() +
  geom_smooth(method = "lm") +
  theme_minimal()
#> `geom_smooth()` using formula = 'y ~ x'



# model

fit <- lm(deny ~ pirat,d)
summary(fit)
#> 
#> Call:
#> lm(formula = deny ~ pirat, data = d)
#> 
#> Residuals:
#>      Min       1Q   Median       3Q      Max 
#> -0.73070 -0.13736 -0.11322 -0.07097  1.05577 
#> 
#> Coefficients:
#>             Estimate Std. Error t value Pr(>|t|)    
#> (Intercept) -0.07991    0.02116  -3.777 0.000163 ***
#> pirat        0.60353    0.06084   9.920  < 2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 0.3183 on 2378 degrees of freedom
#> Multiple R-squared:  0.03974,    Adjusted R-squared:  0.03933 
#> F-statistic: 98.41 on 1 and 2378 DF,  p-value: < 2.2e-16

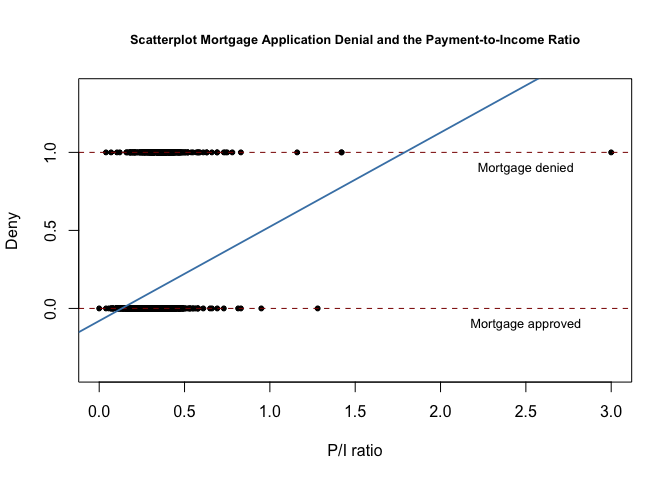
# plot from text
plot(x = d$pirat, 
     y = d$deny,
     main = "Scatterplot Mortgage Application Denial and the Payment-to-Income Ratio",
     xlab = "P/I ratio",
     ylab = "Deny",
     pch = 20,
     ylim = c(-0.4, 1.4),
     cex.main = 0.8)

# add horizontal dashed lines and text
abline(h = 1, lty = 2, col = "darkred")
abline(h = 0, lty = 2, col = "darkred")
text(2.5, 0.9, cex = 0.8, "Mortgage denied")
text(2.5, -0.1, cex= 0.8, "Mortgage approved")

# add the estimated regression line
abline(fit,
       lwd = 1.8, 
       col = "steelblue")



# print robust coefficient summary
coeftest(fit, vcov. = vcovHC, type = "HC1")
#> Error in coeftest(fit, vcov. = vcovHC, type = "HC1"): could not find function "coeftest"

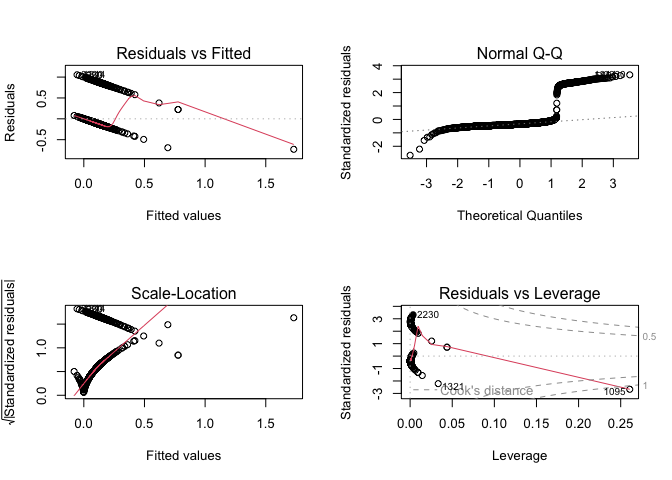
# standard plots (not in text)
par(mfrow = c(2,2))
plot(fit)

The claim is that the model be interpreted as evidence that each 1% (0.01) increase in the variable pirat increases the probability of denial of a loan application by 0.00604, or 0.6%.

Is that useful information in light of the data? Time for a reality check. There's some bad data

> d[d[2] > 1,]
     deny pirat
621     1  1.16
1095    1  3.00
1321    0  1.28
1928    1  1.42
1929    1  1.42

Even during the height of the mortgage lending craze loans with payment terms amounting to 128% of income were not extended. And, of course the other applications above 100% were rejected. In fact, the "back-end debt-to-income ratio was used and it added to payments of principal and interest credit card, auto loan, student loan and all other disclosed debt. The soft cut-off for that ratio was 38% and of the last 125,000 loan summaries I looked at 55% was the highest I ever saw.

This matters because of the reality distortion field that may be generated. To test, I subset to exclude values greater than 50%. I found that doing so approximately doubled the probability of denial of a loan application for each 1% increase in the P/I ratio. A cautionary tale the moral of which is that while the data may not lie, they are entirely capable of deceit.

Several points to note on the standard diagnostic plot

  1. As noted in the text R^2 has no interpretation
  2. Although linear in the parameters, the residuals vs. fitted plot doesn't cluster around zero
  3. QQ plot shows residuals are not normally distributed
  4. Scale-location shows heteroskedascity to the max
  5. The outliers in residuals vs. leverage probably indicate the influence of the anomolously large values of the variable pirat

The model also predicts probabilities of denial in excess of 1.

(Left as an exercise—divide the data into training and test sets and compare predictions of the test data to the observed results and compare RMSE to just the proportions in a two-way contingency table.)

The two principal arguments advanced in the case of the linear probability model are simplicity and robustness. We no longer use desk calculators, so the first argument can be dismissed out of hand. Robustness cannot compensate for a non-normal distribution of residuals. Brushed aside is the usually untenable assumption that the u term can be ignored in the calculations and usable results can be obtained by assuming away not only any influence of other variables but their existence also and treating the model as entirely endogenous. As my country cousins say that dog won't hunt.

And that's even before confronting the principal difficulty in the case presented by the OP, which is that not only is the response variable binary, so is the variable being regressed against.

Just. Don't. Go. There.

15

It's always good to learn from @technocrat, so I hope this isn't too much thread drift. Let me go through some pieces I get and some I don't. And I should say that I personally prefer a logit or a probit to a linear probability model, agreeing I think with @technocrat on that, but many of my colleagues don't.

Stuff I get:

  1. Looking a the deny/pirat diagrams we see that sometimes one gets a prediction outside zero or one. That's a bad thing and something that can't happen with logit/probit.

  2. The point about there apparently being some bad data is a very good one. Very high payment-to-income ratios are indeed nuts. Could be data errors. Could be the very rare cases where someone has low income but very high wealth. In any event, it is hard to believe that they belong in the same model as the rest of the data.

  3. Scale-location shows heteroskedascity to the max

Good point. Linear probability models almost always have heteroskedasticity. That's why in academic practice heteroskedasticity -robust standard errors are used. This has an effect on the computed standard errors, but not the coefficient estimates of course.

Some things I don't understand:

(A)

Not sure I've ever seen a linear regression without an error term. So I'm really not following.

(B)

The formula is linear in its parameters, not
Y = β_0 +β_1x^2+u

Maybe I'm misreading. That formula is exactly linear in its parameters, \beta_0 and \beta_1.

(C)

QQ plot shows residuals are not normally distributed... Robustness cannot compensate for a non-normal distribution of residuals

No argument about the facts, but why would we much care whether the error terms are normally distributed?

(D)

principal difficulty ... is that not only is the response variable binary, so is the variable being regressed against.

I'm just lost here. Binary variables show up on the right of regressions all the time. What's the problem?

(For those still reading, I want to be clear that I learn a lot from @technocrat, so I hope the tone doesn't come over as anything other than friendly. Maybe others want to chime in as well, or maybe move to a different thread since much of this goes beyond what the OP probably needs.)

16

Possibly just to prove I should be finding a better way to spend my time :grinning:, here's a little simulation I wrote.

# lpmSim.R
# Dick Startz
# April 2023

nobs <- 10000 # number of observations
male <- runif(nobs)>0.5 # generate binary male variable

pRedIfMale <- 0.4 # prob male crosses on red
pRedIfFemale <- 0.2

crosses <- rbinom(nobs,size = 1, pRedIfMale)*male +
  rbinom(nobs,size = 1, pRedIfFemale)*(1-male)
      # generate outcome
lpm <- lm(crosses~male)
summary(lpm)

lm(formula = crosses ~ male)

Residuals:
    Min      1Q  Median      3Q     Max 
-0.4032 -0.4032 -0.2030  0.5968  0.7970 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 0.203003   0.006348   31.98   <2e-16 ***
maleTRUE    0.200194   0.008973   22.31   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.4487 on 9998 degrees of freedom
Multiple R-squared:  0.04742,	Adjusted R-squared:  0.04733 
F-statistic: 497.8 on 1 and 9998 DF,  p-value: < 2.2e-1

The true probability in the simulation is 0.2 for women and 0.4 for men. The estimated values are 0.203 and 0.403.

17

Hi, Richard @startz,

Yeah, why don't we start a discussion thread on the topic of binary response variables—this comes up often enough that it may be helpful to collect the ideas centrally. Do you want to pose the question or should I?

To tie it off here on your (D) — the problem isn't a binary on the right side but on both sides. Even the linear probability model has a continuous variable on the right side.

(Reciprocal props to you for taking my Pauli quote in good spirit; never hesitate to throw it back in my face when I'm playing Pope speaking ex cathedra.)

1 Like
18

Why don't you start a thread and lay out what you see to be the controversies. Or maybe pick the one you think most important to get it started.

(And I had to look up the quote, so I'm already ahead for having learned something new.)

2 Likes
19

It is a word every Psych grad student needs to know so that they can nod knowledgeably in a seminar or toss in the word casually in a conversation over coffee. :innocent:.

3 Likes
20

It also may have application in gender studies

21

Actually, a friend of mine ran into such problems in organic chemistry. I did not inquire too closely.

1 Like