Hello,
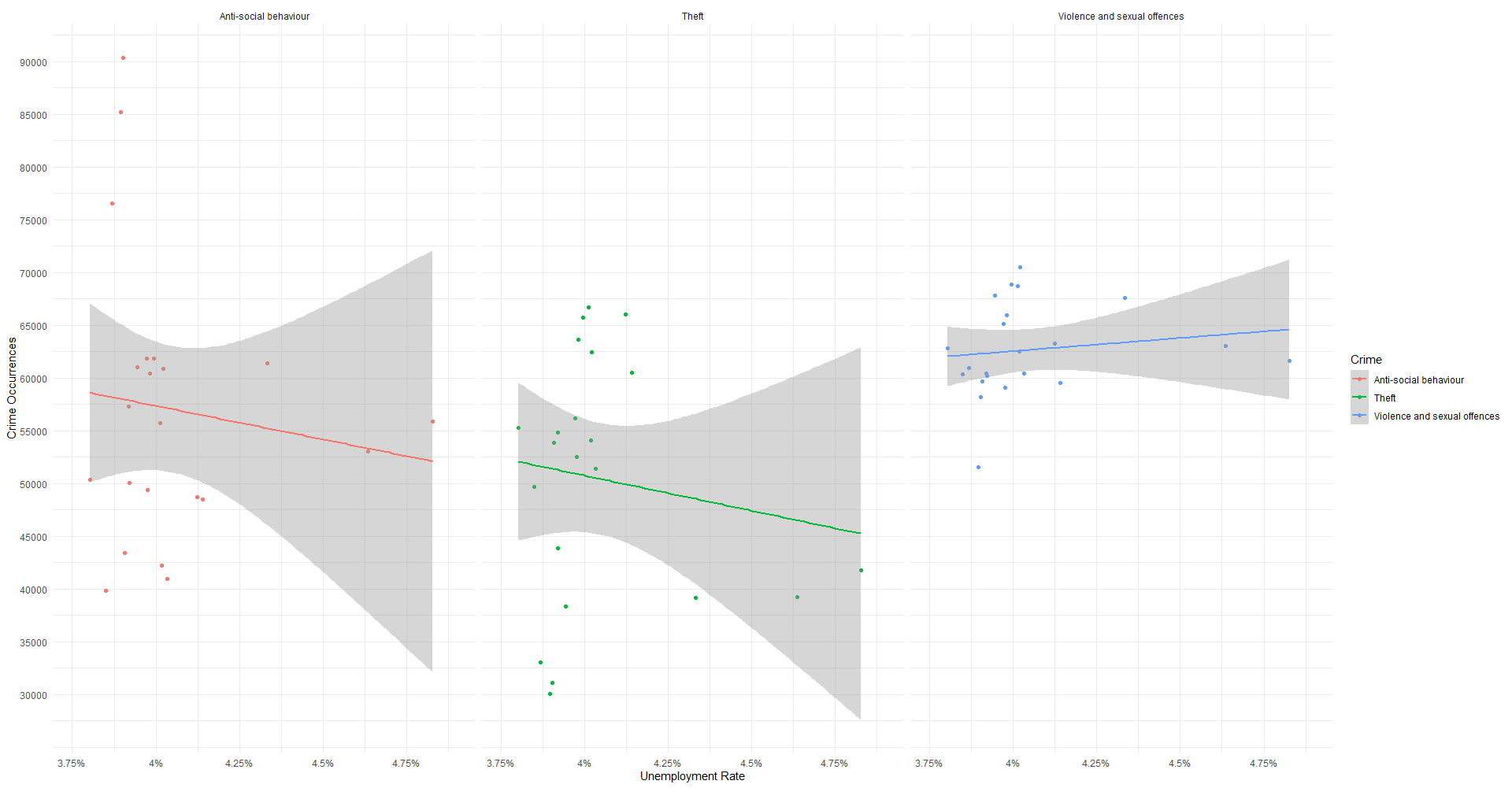
this is the output of a faceted scatter plot with a linear regression in each graph, aimed at studying the potential relationship between Unemployment Rate and Crime Rate for 3 different types of crimes: Anti-Social Behaviour, Theft, and Violence & Sexual Offences.
Here's the plot and its output, and my interpretation follows:
`Call:`
`lm(formula = Crime_occurrences ~ Unemployment_rate + Crime, data = df)`
`Residuals:`
`Min 1Q Median 3Q Max`
`-20871 -6755 362 4597 32818`
`Coefficients:`
`Estimate Std. Error t value Pr(>|t|)`
`(Intercept) 71252 21686 3.286 0.00168 **`
`Unemployment_rate -3508 5327 -0.658 0.51267`
`CrimeTheft -6613 3180 -2.080 0.04169 *`
`CrimeViolence and sexual offences 5606 3180 1.763 0.08287 .`
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 10550 on 62 degrees of freedom
Multiple R-squared: 0.1972, Adjusted R-squared: 0.1584
F-statistic: 5.077 on 3 and 62 DF, p-value: 0.003301
My interpretation:
-
t value is extremely low, suggesting no relationship between the two variables
-
Pr(>|t|)is <0.05 for THEFT, suggesting a relationship between that and unemployment rate -
R-squared is very low, suggesting that the linear regression line wasn't that succesful at capturing the values in the scatter plot (i.e. the residuals are all over the place, which is true; another sign of no relationship)
-
F is fairly low, suggesting no relationship
-
p value is <0.05, suggesting a strong relationship
My questions:
-
Where is "Anti-Social Behaviour"? It's in my data frame but not in this output
-
What does the p value refer to? Unemployment rate and WHICH type of Crime?
-
How should I interpret the discrepancy between Theft
Pr(>|t|)being <0.05 but t value being not only low, but even negative?
Any suggestions would be highly appreciated!