I have this sample data -
> dput(my_vec)
c(7.16523478153752, 5.66659652818595, 4.47575534893755, 4.84970857977856,
15.2276296414708, -0.573093658844655, 4.97980673868322, 2.73969325233614,
5.14683035133365, 10.1221488713611, 9.01656611721311, 65.711819422978,
5.52057043354834, 6.30674880627702, 8.67771771267678, 5.2528503049587,
3.50395623925858, 4.24774012371174, 11.4137624410312, -48.1722033880239,
-0.376400642113356, 5.76475359419462, -27.353313803102, 4.09682042042852,
5.03373747558625, 3.8261660769812, 4.43580895525249, 4.22242932760446,
4.44905425775097, 4.98475525084258, 3.6416524979406, 3.81767927422987,
-93.2141354888589, 5.01103555428068, 5.38206564752185, 3.0296536606134,
86.676038167071, 3.76536864898752, 7.26590572567999, 4.63759338498908,
-17.2259677581435, 4.90903933854569, 4.43042810097151, 5.41519101700693,
7.01553803666926, 5.05370712380939, 5.22896180532498, 3.92429687923716,
5.46452912130986, 4.50524864464907, 6.13119216629816, 6.931011365041,
5.70039361940988, 6.12470771804837, 6.66119827017415, -4.26865103703534,
4.77160581324527, 7.91297525486072, 7.04882594451997, -98.2224152538262,
6.22663920777969, 5.77535246011091, -9.91868097075743, 7.77803716672203,
-10.1297033914588, 4.56699263921898, 8.56120643036614, 2.28239965661689,
5.6212927060249, 5.42419784358529, 5.3654428914847, 3.89730116338776,
3.93504254066386, 4.38168766024675, 3.00038017933155, 4.81884527713388,
4.45257297902316, -3.50516232920359, 6.07365636649988, 4.26195094225287,
4.73753258557777, 0.807607628402986, 3.93740907315333, 3.08283749617447,
3.77379774203008, 2.56562208889432, -19.6532587812275, 8.00379422844706,
5.27350155029373, 5.17570743606727, 6.49856446395129, -8.78462344722329,
4.38775671122269, 4.39685118092286, 3.52571990926583, 7.13834590807858,
0.724655622024244, 5.72807728660989, 6.58172179467414, 6.22426074825281
)
and, I need to estimate theta from our sample ( our data is the sample ) , with Newton Rapson method. theta parameter comes from a Cauchi distribution, when my initial value is the mean of the sample.
I wrote something like this -
> data<-read.table(file.choose(), header = TRUE, sep= "")
> my_vec<-as.numeric(as.character(unlist(data[[1]])))
> dput(my_vec)
> nr_method<-function(x,toler=.001){ #x is a vector here
> start_value<-median(x)
> n=length(x);
> theta=start_value;
> # Compute first deriviative of log likelihood
> first_derivate<-2*sum((x-theta)/(1+(x-theta)^2))
> # Continue Newton’s method until the first derivative
> while(abs(first_derivate)>toler){
> # Compute second derivative of log likelihood
> second_derivate=2*sum(((x-theta)^2-1)/(1+(x-theta)^2)^2);
> # Newton’s method update of estimate of theta
> theta_new<-theta-first_derivate/second_derivate;
> theta=theta_new;
> # Compute first derivative of log likelihood
> first_derivate=2*sum((x-theta)/(1+(x-theta)^2))
> }
> list(theta_hat=theta);
> }
> main_fun <- function (theta, x)
> {
> sum (-log(1+(x-theta)^2))
> }
> th<-seq(-15,15,by=0.1)
> ll<-rep(0,length(th))
> for (i in 1:length(th)) ll[i] <- main_fun(th[i],x)
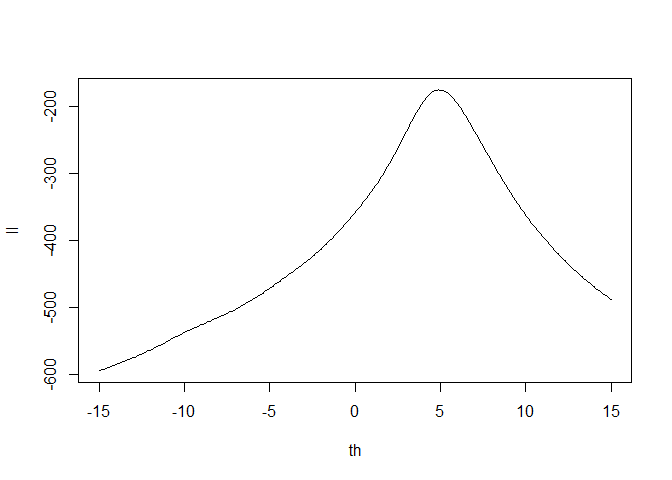
> plot(th,ll,type="l")
> try1<-nr_method(x,1e-5)
but I don't know ho to contunie from here.
Finanlly, I neeed to plot the likelihood, and make sure I found the max.
any help?