Thanks for working with me. I've posted an edited and heavily commented reprex based on yours. I can reproduce the error. I have an idea what causes it, but have found no fix for the h = 1 argument. The tedious details follow.
Let's approach this from a more abstract stance: f(x) = y. In R terms these are three objects, one of which is of class function.
x is what is at hand: my_example_ts
y is what is desired: this is unclear because we are stuck on the error
f is the function (which may be a combination of functions) that turns x into y
An intermediate object seems to be something that can be used as a beginning index for a loop.
In my experience, however, questions about what to do are much more fruitful than how to do. In this case, what is y? What are you trying to change my_sample_ts, the original time series into?
#### practice tip--always start testing in a new session
#### after saving code (preferably into a version control
#### system). This avoids having namespace confusion
#### code reformatted for readability
#### using styler package and start-up
#### messages omitted; this is a matter
#### of style, but consistency in coding
#### is recommended for ease of debugging
suppressPackageStartupMessages({
library(forecast)
library(dplyr) #### added for debugging
library(lubridate) #### added for debugging
library(purrr) #### added for debugging
})
##### DO NOT USE BUILT-IN FUNCTION NAMES
##### my_sample, df, data and others may be treated as closures
##### in some operations; not a problem here but it is something
##### to avoid
my_sample <- c(
997.791666085149, 999.366182253824, 1000.46381043618, 993.705371491957,
996.740285547083, 1003.4906422465, 1005.34156334679, 997.604304813648,
1009.6643663447, 993.128043433675, 1005.53114457311, 1004.714338528,
1017.72437048901, 1007.94598223837, 988.226025380339, 994.785531675548,
1011.97940179699, 998.636119804733, 994.062327383755, 993.979060157697,
1003.93555180002, 1001.70926154818, 997.933817810478, 979.693838855987,
992.823376865983, 997.838580296017, 1006.21213228311, 991.977377944057,
1003.77529414578, 1002.67024480564, 989.082946231366, 989.680523087659,
990.781349841785, 1005.75606421591, 997.035360314707, 994.928511836986,
996.012597263487, 994.249532642942, 1005.95070720716, 988.48958339183,
997.279197474874, 993.176463294942, 1007.25434521494, 1003.7052774576,
999.078187434345, 1004.91757624002, 1008.88416631965, 1007.04637128748,
1003.12247450407, 1015.17660495696, 1001.97021341098, 997.376118405193,
992.973077430376, 994.981878550185, 1003.15585020888, 1007.42839140189,
1008.82349023285, 1009.50815752809, 998.249912313893, 996.130572881505,
998.1908524304, 1004.27183684979, 1000.25755061327, 999.546581914197,
999.586563241259, 987.790001893712, 999.151672336352, 1001.78375990166,
999.719712907908, 1006.48174402213, 1003.59120454781, 998.954072595588,
1008.72600016238, 1006.72562410066, 1006.89970982311, 1005.21317048907,
1003.9871376226, 1007.50194110916, 995.716626103823, 994.981330040876,
1000.95853471046, 1000.34298358716, 1004.89210023244, 997.67098695885,
999.613667330844, 992.356606521014, 997.889751087205, 999.572103909505,
1011.73124586553, 1000.92379332441, 998.47164223236, 993.927783786705,
990.932274895557, 995.044718031122, 995.990214970003, 996.671678002519,
1015.14438283045, 997.18825887884, 991.291688264167, 1012.20878626223,
997.791666085149, 999.366182253824, 1000.46381043618, 993.705371491957,
996.740285547083, 1003.4906422465, 1005.34156334679, 997.604304813648,
1009.6643663447, 993.128043433675, 1005.53114457311, 1004.714338528,
1017.72437048901, 1007.94598223837, 988.226025380339, 994.785531675548,
1011.97940179699, 998.636119804733, 994.062327383755, 993.979060157697,
1003.93555180002, 1001.70926154818, 997.933817810478, 979.693838855987,
992.823376865983, 997.838580296017, 1006.21213228311, 991.977377944057,
1003.77529414578, 1002.67024480564, 989.082946231366, 989.680523087659,
990.781349841785, 1005.75606421591, 997.035360314707, 994.928511836986,
996.012597263487, 994.249532642942, 1005.95070720716, 988.48958339183,
997.279197474874, 993.176463294942, 1007.25434521494, 1003.7052774576,
999.078187434345, 1004.91757624002, 1008.88416631965, 1007.04637128748,
1003.12247450407, 1015.17660495696, 1001.97021341098, 997.376118405193,
992.973077430376, 994.981878550185, 1003.15585020888, 1007.42839140189,
1008.82349023285, 1009.50815752809, 998.249912313893, 996.130572881505,
998.1908524304, 1004.27183684979, 1000.25755061327, 999.546581914197,
999.586563241259, 987.790001893712, 999.151672336352, 1001.78375990166,
999.719712907908, 1006.48174402213, 1003.59120454781, 998.954072595588,
1008.72600016238, 1006.72562410066, 1006.89970982311, 1005.21317048907,
1003.9871376226, 1007.50194110916, 995.716626103823, 994.981330040876,
1000.95853471046, 1000.34298358716, 1004.89210023244, 997.67098695885,
999.613667330844, 992.356606521014, 997.889751087205, 999.572103909505,
1011.73124586553, 1000.92379332441, 998.47164223236, 993.927783786705,
990.932274895557, 995.044718031122, 995.990214970003, 996.671678002519,
1015.14438283045, 997.18825887884, 991.291688264167, 1012.20878626223,
997.791666085149, 999.366182253824, 1000.46381043618, 993.705371491957,
996.740285547083, 1003.4906422465, 1005.34156334679, 997.604304813648
)
#### practice tip: when debugging inspect the output of each step
str(my_sample)
#> num [1:208] 998 999 1000 994 997 ...
#### this confirms we have a numeric vector
#### help("ts") shows that a numeric vector is a permitted argument
##### frequency is the unit of observation; 52 in this case signifies
##### 52 observations per day
##### that is slightly more frequent than every half-hour
##### is that what you really want?
my_sample_ts <- ts(my_sample, start = c(2016, 1), end = c(2019, 52), frequency = 52)
#### inspect to see if it is as intended
head(my_sample_ts)
#> Time Series:
#> Start = c(2016, 1)
#> End = c(2016, 6)
#> Frequency = 52
#> [1] 997.7917 999.3662 1000.4638 993.7054 996.7403 1003.4906
length(my_sample_ts)
#> [1] 208
##### style suggestion: reserve the names x and y for
##### argument names within functions, as they are often
##### used for plotting, for example
##### begin debugging
##### practice tip: comment in function signature
#############################################################
# help("window")
# ## S3 replacement method for class 'ts'
# window(x, start, end, frequency, deltat, ...) <- value
#
# Arguments
# x a time-series (or other object if not replacing values).
#
# start the start time of the period of interest.
#
# end the end time of the period of interest.
#
# frequency, deltat the new frequency can be specified by either (or both if they are consistent).
#### when working in RStudio, keep the help page open, alternatively
#### and, in any event, check the details and value sections
my_x <- window(my_sample_ts, end = c(2018, 52) + (4 - 1) / 52)
#### check output
head(my_x)
#> Time Series:
#> Start = c(2016, 1)
#> End = c(2016, 6)
#> Frequency = 52
#> [1] 997.7917 999.3662 1000.4638 993.7054 996.7403 1003.4906
length(my_x)
#> [1] 159
#### this returns a time series object starting c(2016,1) and
#### ending c(2019,3)
#### does this make sense?
#### the starting point is what date?
#### is it consistent with the frequency?
#### evaluate each part; use a function since
#### we'll be doing this again for testing
test_fun <- function(x) {
(x - 1) / 52
}
test_fun(4)
#> [1] 0.05769231
#### what impact does a number this small have?
#### what impact is it intended to have
#### how this expression changes as the first number varies
seq(1:53) %>% map(., test_fun) %>% unlist() -> test_out
test_out
#> [1] 0.00000000 0.01923077 0.03846154 0.05769231 0.07692308 0.09615385
#> [7] 0.11538462 0.13461538 0.15384615 0.17307692 0.19230769 0.21153846
#> [13] 0.23076923 0.25000000 0.26923077 0.28846154 0.30769231 0.32692308
#> [19] 0.34615385 0.36538462 0.38461538 0.40384615 0.42307692 0.44230769
#> [25] 0.46153846 0.48076923 0.50000000 0.51923077 0.53846154 0.55769231
#> [31] 0.57692308 0.59615385 0.61538462 0.63461538 0.65384615 0.67307692
#> [37] 0.69230769 0.71153846 0.73076923 0.75000000 0.76923077 0.78846154
#> [43] 0.80769231 0.82692308 0.84615385 0.86538462 0.88461538 0.90384615
#> [49] 0.92307692 0.94230769 0.96153846 0.98076923 1.00000000
#### visualize
plot(seq(1:53), test_out)
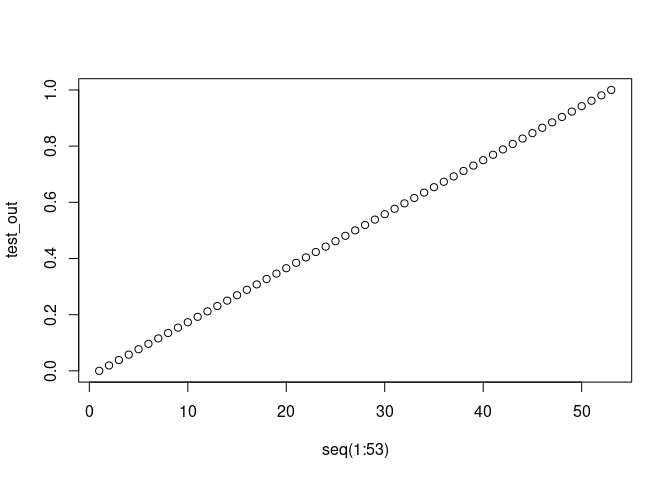
#### assessment
#### the expression linearly increases to 1 in the range 1:53
#### with the range 1:521, the expression maximizes to 10
##### IDENTIFICATION OF THE ERROR
##### CAUTION: GETTING THE QUESTION RIGHT MAY
##### MAKE THE ERROR IRRELEVANT
# The error occurs only if you use 4,8 or 12. For all other numbers the whole code runs perfectly
#### practice suggestion: convert to a function; when more
#### options are to be tried, can be modified--for ic, for
#### example; minimizes syntax errors once working
#### Note the function signature in help
#### there are many more than used here
#### probably not helpful to cut-and-paste
#### here
#### CRUCIAL: auto.arima takes a univariate time series
#### as a mandatory argument
refit <- function(x) {
auto.arima(x,
ic = c("bic"),
stepwise = FALSE,
approximation = TRUE,
lambda = "auto",
biasadj = TRUE
)
}
#### note: this is long running
refitted <- refit(my_x)
#### inspect
class(refitted)
#> [1] "forecast_ARIMA" "ARIMA" "Arima"
#### signature check
#### a time series or ***time series model*** for which forecasts are required
#### another function suggestion
mk_arima <- function(x,y) {
forecast(x,
h = y,
lambda = x$lambda)
}
### testing with "forecast_ARIMA" "ARIMA" "Arima" object
### and an argument h = 1
mk_arima(refitted,1)$mean
#> Warning in .cbind.ts(list(e1, e2), c(deparse(substitute(e1))[1L],
#> deparse(substitute(e2))[1L]), : non-intersecting series
#> Error in NextMethod(.Generic): cannot assign 'tsp' to zero-length vector
### SUCCESS! error for h=1 reproduced
### retest with h=2
mk_arima(refitted,2)$mean -> a
### SUCCESS! no error
### QUESTION: is a time series of two values desired?
### retest with another odd number
mk_arima(refitted,3)$mean
#> Time Series:
#> Start = c(2019, 4)
#> End = c(2019, 6)
#> Frequency = 52
#> [1] 999.4212 1000.1001 1000.1001
### QUESTION: is there a reason to discard the confidence intervals?
mk_arima(refitted,3)
#> Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
#> 2019.058 999.4212 990.6408 1008.171 985.9486 1012.761
#> 2019.077 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.096 1000.1001 991.1562 1009.013 986.3757 1013.686
### test for next 10 values of h
mk_arima(refitted,4)
#> Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
#> 2019.058 999.4212 990.6408 1008.171 985.9486 1012.761
#> 2019.077 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.096 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.115 1000.1001 991.1562 1009.013 986.3757 1013.686
mk_arima(refitted,5)
#> Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
#> 2019.058 999.4212 990.6408 1008.171 985.9486 1012.761
#> 2019.077 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.096 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.115 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.135 1000.1001 991.1562 1009.013 986.3757 1013.686
mk_arima(refitted,6)
#> Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
#> 2019.058 999.4212 990.6408 1008.171 985.9486 1012.761
#> 2019.077 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.096 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.115 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.135 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.154 1000.1001 991.1562 1009.013 986.3757 1013.686
mk_arima(refitted,7)
#> Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
#> 2019.058 999.4212 990.6408 1008.171 985.9486 1012.761
#> 2019.077 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.096 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.115 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.135 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.154 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.173 1000.1001 991.1562 1009.013 986.3757 1013.686
mk_arima(refitted,8)
#> Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
#> 2019.058 999.4212 990.6408 1008.171 985.9486 1012.761
#> 2019.077 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.096 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.115 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.135 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.154 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.173 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.192 1000.1001 991.1562 1009.013 986.3757 1013.686
mk_arima(refitted,9)
#> Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
#> 2019.058 999.4212 990.6408 1008.171 985.9486 1012.761
#> 2019.077 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.096 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.115 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.135 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.154 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.173 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.192 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.212 1000.1001 991.1562 1009.013 986.3757 1013.686
mk_arima(refitted,10)
#> Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
#> 2019.058 999.4212 990.6408 1008.171 985.9486 1012.761
#> 2019.077 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.096 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.115 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.135 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.154 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.173 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.192 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.212 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.231 1000.1001 991.1562 1009.013 986.3757 1013.686
mk_arima(refitted,11)
#> Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
#> 2019.058 999.4212 990.6408 1008.171 985.9486 1012.761
#> 2019.077 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.096 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.115 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.135 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.154 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.173 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.192 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.212 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.231 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.250 1000.1001 991.1562 1009.013 986.3757 1013.686
mk_arima(refitted,12)
#> Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
#> 2019.058 999.4212 990.6408 1008.171 985.9486 1012.761
#> 2019.077 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.096 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.115 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.135 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.154 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.173 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.192 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.212 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.231 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.250 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.269 1000.1001 991.1562 1009.013 986.3757 1013.686
mk_arima(refitted,13)
#> Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
#> 2019.058 999.4212 990.6408 1008.171 985.9486 1012.761
#> 2019.077 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.096 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.115 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.135 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.154 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.173 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.192 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.212 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.231 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.250 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.269 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.288 1000.1001 991.1562 1009.013 986.3757 1013.686
#### No errors
#### Why does h = 1 this row the error?
#### begin with the question: what role does this argument play
#### in the forecast function?
#### "Number of periods for forecasting"
#### Let's use an example from help("forecast")
fit <- ets(window(WWWusage, end=60))
forecast(WWWusage, model=fit)
#> Model is being refit with current smoothing parameters but initial states are being re-estimated.
#> Set 'use.initial.values=TRUE' if you want to re-use existing initial values.
#> Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
#> 101 218.3960 213.9345 222.8575 211.5727 225.2193
#> 102 217.1137 207.9338 226.2936 203.0743 231.1532
#> 103 216.0879 201.8561 230.3197 194.3223 237.8536
#> 104 215.2673 195.8853 234.6493 185.6251 244.9095
#> 105 214.6107 190.1127 239.1088 177.1442 252.0773
#> 106 214.0855 184.5805 243.5905 168.9615 259.2095
#> 107 213.6654 179.3037 248.0271 161.1137 266.2170
#> 108 213.3292 174.2817 252.3767 153.6112 273.0472
#> 109 213.0603 169.5059 256.6147 146.4496 279.6710
#> 110 212.8452 164.9630 260.7274 139.6157 286.0746
### Observation: h is not a mandatory argument
### What happens if h = 1 is added to the example?
forecast(WWWusage, model=fit, h = 1)
#> Model is being refit with current smoothing parameters but initial states are being re-estimated.
#> Set 'use.initial.values=TRUE' if you want to re-use existing initial values.
#> Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
#> 101 218.396 213.9345 222.8575 211.5727 225.2193
class(WWWusage)
#> [1] "ts"
class(fit)
#> [1] "ets"
### No error
### Conclusion the argument h =1, by itself, does not throw an
### error when used in conjunction with a ts and ets object
### as the sole additional, non-default arguments
#### Let's set aside the possibility that an object of class
#### "forecast_ARIMA" "ARIMA" "Arima" makes a difference
# It works for h=2 but not for h=1; h=1 is needed because this is a part of several different loops
# > Warning in .cbind.ts(list(e1, e2), c(deparse(substitute(e1))[1L],
# > deparse(substitute(e2))[1L]), : non-intersecting series
# > Error in NextMethod(.Generic): kann 'tsp' nicht einem Vektor der Länge 0 zuordnen
#### let's also set aside the warning and focus on the error
#### the function that is throwing the error is from within forecast
#### the function tsp which takes
### a vector or matrix or univariate or multivariate time-series
#### and returns
### a numeric vector of length 3 or NULL
#### let's run some tests
#### using time series
tsp(my_sample_ts)
#> [1] 2016.000 2019.981 52.000
tsp(WWWusage)
#> [1] 1 100 1
#### using models
tsp(fit)
#> NULL
tsp(refitted)
#> NULL
#### using matrix
mdat <- matrix(c(1, 2, 3, 11, 12, 13),
nrow = 2, ncol = 3, byrow = TRUE,
dimnames = list(
c("row1", "row2"),
c("C.1", "C.2", "C.3")
)
)
tsp(mdat)
#> NULL
#### using vector
tsp(c(seq(1:100)))
#> NULL
#### unclear: why matrix and vector return null
#### What is calling tsp?
#### the function mk_arima created here?
#### that is just a convenience wrapper over forecast
mk_arima <- function(x,y) {
forecast(x,
h = y,
lambda = x$lambda)
}
### What happens if we take lambda out of the picture?
mk_arima2 <- function(x,y) forecast(x,h = y)
mk_arima2(refitted,1)
#> Warning in .cbind.ts(list(e1, e2), c(deparse(substitute(e1))[1L],
#> deparse(substitute(e2))[1L]), : non-intersecting series
#> Error in NextMethod(.Generic): cannot assign 'tsp' to zero-length vector
mk_arima2(refitted,2)
#> Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
#> 2019.058 999.4212 990.6408 1008.171 985.9486 1012.761
#> 2019.077 1000.1001 991.1562 1009.013 986.3757 1013.686
### no difference
### What happens if we dispense with h altogether?
forecast(refitted)
#> Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
#> 2019.058 999.4212 990.6408 1008.171 985.9486 1012.761
#> 2019.077 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.096 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.115 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.135 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.154 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.173 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.192 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.212 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.231 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.250 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.269 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.288 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.308 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.327 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.346 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.365 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.385 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.404 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.423 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.442 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.462 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.481 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.500 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.519 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.538 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.558 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.577 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.596 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.615 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.635 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.654 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.673 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.692 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.712 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.731 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.750 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.769 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.788 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.808 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.827 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.846 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.865 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.885 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.904 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.923 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.942 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.962 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2019.981 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.000 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.019 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.038 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.058 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.077 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.096 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.115 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.135 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.154 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.173 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.192 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.212 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.231 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.250 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.269 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.288 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.308 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.327 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.346 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.365 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.385 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.404 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.423 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.442 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.462 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.481 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.500 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.519 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.538 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.558 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.577 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.596 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.615 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.635 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.654 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.673 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.692 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.712 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.731 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.750 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.769 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.788 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.808 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.827 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.846 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.865 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.885 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.904 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.923 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.942 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.962 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2020.981 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2021.000 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2021.019 1000.1001 991.1562 1009.013 986.3757 1013.686
#> 2021.038 1000.1001 991.1562 1009.013 986.3757 1013.686
### the result is identical to h = 2, 3 ... in a series
### what dates are these?
the_dates <- c(2019.058,2019.077,2019.096,2019.115,2019.135,2019.154,2019.173,2019.192,2019.212,2019.231,2019.250,2019.269,2019.288,2019.308,2019.327,2019.346,2019.365,2019.385,2019.404,2019.423,2019.442,2019.462,2019.481,2019.500,2019.519,2019.538,2019.558,2019.577,2019.596,2019.615,2019.635,2019.654,2019.673,2019.692,2019.712,2019.731,2019.750,2019.769,2019.788,2019.808,2019.827,2019.846,2019.865,2019.885,2019.904,2019.923,2019.942,2019.962,2019.981,2020.000,2020.019,2020.038,2020.058,2020.077,2020.096,2020.115,2020.135,2020.154,2020.173,2020.192,2020.212,2020.231,2020.250,2020.269,2020.288,2020.308,2020.327,2020.346,2020.365,2020.385,2020.404,2020.423,2020.442,2020.462,2020.481,2020.500,2020.519,2020.538,2020.558,2020.577,2020.596,2020.615,2020.635,2020.654,2020.673,2020.692,2020.712,2020.731,2020.750,2020.769,2020.788,2020.808,2020.827,2020.846,2020.865,2020.885,2020.904,2020.923,2020.942,2020.962,2020.981,2021.000,2021.019,2021.038)
format(date_decimal(the_dates), "%Y-%m-%d")
#> [1] "2019-01-22" "2019-01-29" "2019-02-05" "2019-02-11" "2019-02-19"
#> [6] "2019-02-26" "2019-03-05" "2019-03-12" "2019-03-19" "2019-03-26"
#> [11] "2019-04-02" "2019-04-09" "2019-04-16" "2019-04-23" "2019-04-30"
#> [16] "2019-05-07" "2019-05-14" "2019-05-21" "2019-05-28" "2019-06-04"
#> [21] "2019-06-11" "2019-06-18" "2019-06-25" "2019-07-02" "2019-07-09"
#> [26] "2019-07-16" "2019-07-23" "2019-07-30" "2019-08-06" "2019-08-13"
#> [31] "2019-08-20" "2019-08-27" "2019-09-03" "2019-09-10" "2019-09-17"
#> [36] "2019-09-24" "2019-10-01" "2019-10-08" "2019-10-15" "2019-10-22"
#> [41] "2019-10-29" "2019-11-05" "2019-11-12" "2019-11-20" "2019-11-26"
#> [46] "2019-12-03" "2019-12-10" "2019-12-18" "2019-12-25" "2020-01-01"
#> [51] "2020-01-07" "2020-01-14" "2020-01-22" "2020-01-29" "2020-02-05"
#> [56] "2020-02-12" "2020-02-19" "2020-02-26" "2020-03-04" "2020-03-11"
#> [61] "2020-03-18" "2020-03-25" "2020-04-01" "2020-04-08" "2020-04-15"
#> [66] "2020-04-22" "2020-04-29" "2020-05-06" "2020-05-13" "2020-05-20"
#> [71] "2020-05-27" "2020-06-03" "2020-06-10" "2020-06-18" "2020-06-25"
#> [76] "2020-07-02" "2020-07-08" "2020-07-15" "2020-07-23" "2020-07-30"
#> [81] "2020-08-06" "2020-08-13" "2020-08-20" "2020-08-27" "2020-09-03"
#> [86] "2020-09-10" "2020-09-17" "2020-09-24" "2020-10-01" "2020-10-08"
#> [91] "2020-10-15" "2020-10-22" "2020-10-29" "2020-11-05" "2020-11-12"
#> [96] "2020-11-19" "2020-11-26" "2020-12-03" "2020-12-10" "2020-12-18"
#> [101] "2020-12-25" "2021-01-01" "2021-01-07" "2021-01-14"
#### What would be the date before 2019-058, 2019-01-22, a week earlier
#### BIG QUESTION: why can't that date be calculated?
#### It's being calculated from our variable refitted, but what part?
forecast(refitted$fitted)
#> Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
#> 2019.058 1000.7522 999.3853 1002.1192 998.6617 1002.843
#> 2019.077 999.9741 998.6071 1001.3410 997.8835 1002.065
#> 2019.096 1001.2251 999.8582 1002.5921 999.1346 1003.316
#****************omitted to remain within space limits*********************
#> 2021.038 1000.4975 999.1305 1001.8644 998.4069 1002.588
#### NOTE: this displays the same FORM of output, but note that
#### Unlike forecast(refitted), which has identical values after
#### the first row, refitted$fitted has different values for each
#### row
#### another interesting twist
class(refitted$fitted)
#> [1] "ts"
forecast(refitted$fitted, h = 1)
#> Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
#> 2019.058 1000.752 999.3853 1002.119 998.6617 1002.843
class(my_sample_ts)
#> [1] "ts"
forecast(my_sample_ts, h = 1)
#> Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
#> 2020 999.3768 992.0252 1006.728 988.1336 1010.62
#### time series CAN handle h = 1
#### splitting the question
#### 1. why does forecast choke with h = 1 on the non-ts object?
#### 2. why is it necessary to use a non-ts object?
Created on 2020-11-05 by the reprex package (v0.3.0.9001)
