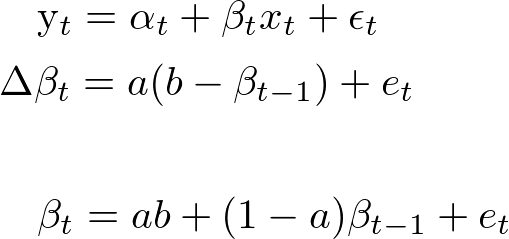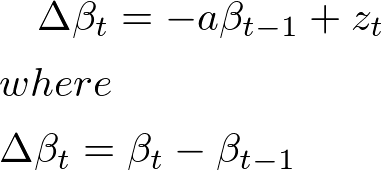I wasn't really getting why you called b the long-term mean of \beta_t, the optimal hedge ratio. I figured it out. \beta_t is an AR(1) process and assuming that it is stationary (i.e. 0 < a <1), its long-term mean is computed as:
\beta_t = ab + (1-a)\beta_{t-1} + e_t \\
E(\beta_t) = \frac{ab}{1 - (1-a)} \\
E(\beta_t) = \frac{ab}{a} \\
E(\beta_t) = b
where ab is the constant and (1-a) is the coefficient of the AR(1) process. So this is MY take on how to tackle your problem. Let me first start with the theoretical side of things. Here is the general matrix representation of dynamic linear models:
y_t = F_t \theta_t + \varepsilon_t \\
\theta_t = G \theta_{t-1} + u_t
where \varepsilon_t and u_t are normally distributed mean zero processes of constant variance. The system under consideration here is a dynamic linear model with a dynamic level (\alpha_t) and a dynamic slope (\beta_t):
y_t = \alpha_t + \beta_t x_t + \epsilon_t \\
\alpha_t = \alpha_{t-1} + v_t \\
\beta_t = ab + (1-a) \beta_{t-1} + w_t
where \epsilon_t, v_t and w_t are normally distributed mean zero processes of constant variance. This system cannot be directly put into the DLM matrix form without a bit of transformation. This is because of the constant term ab in the equation for \beta_t. But it is possible to get rid of it by demeaning \beta_t.
We define \tilde{\beta}_t = \beta_t - b, so the system can be rewritten:
y_t = \alpha_t + \tilde{\beta}_t x_t + \tilde{\epsilon}_t \\
\alpha_t = \alpha_{t-1} + v_t \\
\tilde{\beta}_t = (1-a) \tilde{\beta}_{t-1} + \tilde{w}_t
Note that the constant ab is no longer present. Given our new system, we have:
\theta_t = [\alpha_t \ \ \tilde{\beta}_t]' \\
F_t = [1 \ \ x_t]' \\
G = \begin{bmatrix} 1 & 0 \\ 0 & 1-a \end{bmatrix}
In traditional models such as this one, matrix G is slightly different:
G = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}
So we will have to manually modify the G matrix in the code.
Now that the system has been identified, it is time to do some coding. You mentioned earlier that the data you uploaded was in first differences (y_t - y_{t-1}). I'm having a hard time to accept that because the average values for each of the two price series are: \$217.39 for ASX and \$166.45 for HRW. Whether the currency is US dollars or Australian dollars, it is hard to believe that these prices change by over $100 daily! So I am going to assume that your data is the actual prices, not the first differences.
First, the HRW column has some NA values, which are problematic for the regression model we want to fit. So I am going to impute them with the mice package.
# Load packages
library(dlm)
library(readxl)
library(mice)
# Import the dataset
dat <- read_xlsx(here::here("kalman_filter/Futures202011.xlsx"))
# Impute the NA values
dat[, -1] <- complete(mice(data = dat[, -1]))
# Function for estimating the maximum likelihood parameters
build_model <- function(u){
dlmModReg(X = dat$HRW_c1, dV = exp(u[1]), dW = exp(u[2:3]))
}
mod_mle <- dlmMLE(y = dat$ASX_c1_us, parm = rep(0, 3), build = build_model) # Actual estimation of maximum likelihood parameters
# Build dynamic linear model with MLE parameters
mod <- build_model(u = mod_mle$par)
# Currently matrix G is an identity matrix of size 2...
mod$GG
[,1] [,2]
[1,] 1 0.0
[2,] 0 1
# So we edit it to suit our needs, let's assume a = 0.2 so that 1 - a = 0.8
mod$GG[2, 2] <- 0.8
mod$GG
[,1] [,2]
[1,] 1 0.0
[2,] 0 0.8
# Apply the Kalman filter
mod_filtered <- dlmFilter(y = dat$ASX_c1_us, mod)
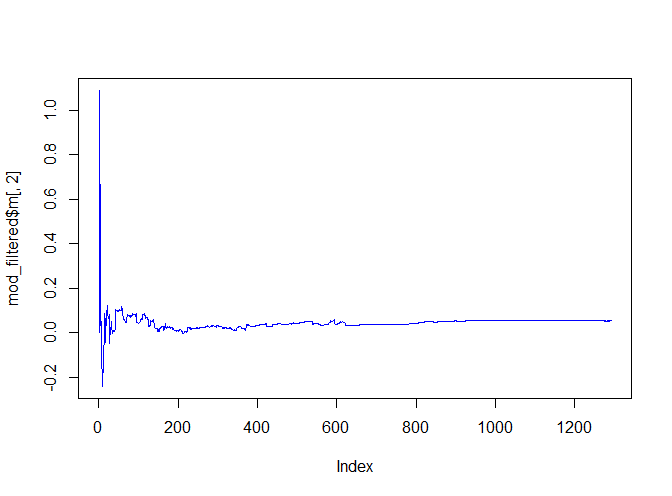
The estimated level and slope coefficients can be obtained with:
mod_filtered$m
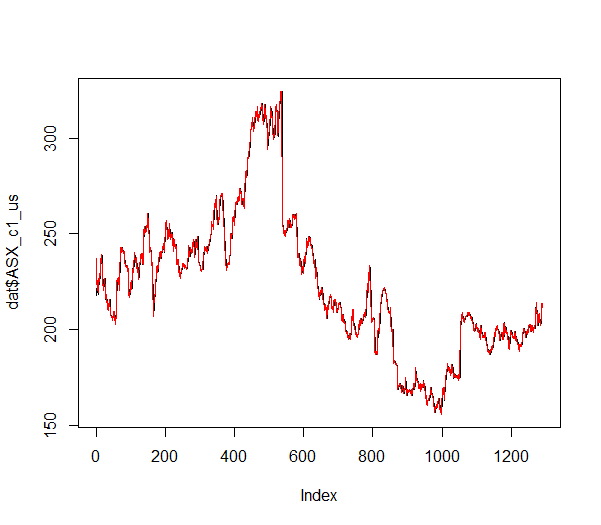
The first column is for the level and the second column is for the slope. This model does a pretty good job fitting the data. In the following visualization, I plot the actual series against the estimated levels (in red):
plot(dat$ASX_c1_us, type = "l")
lines(mod_filtered$m[-(1:2), 1], col = "red")