Determine Statistical Difference Between Two Groups

brant · February 22, 2025, 4:44pm

Hi, I am having trouble calculating a p-value to show statistical differences between sites for an upcoming conference poster. I have suspended solids concentrations for six different sites and created a graph of the mean concentrations for each site (as shown below)

The sample sizes for Inflow 1, Outflow 1, Inflow 2, Outflow 2, Inflow 3, and Outflow 3 are 25, 25, 12, 12, 14, 14, respectively.

I am trying to determine if:

Inflow 1 (n = 25) is statistically different from Outflow 1 (n = 25)
Inflow 2 (n = 12) is statistically different from Outflow 2 (n = 12)
Inflow 3 (n = 14) is statistically different from Outflow 3 (n = 14)

I tried running a Wilcoxon rank-sum test to compare each group, but I am getting the following outputs:

> test_result <- wilcox.test(inflow1, outflow1)
> print(test_result)

	Wilcoxon rank sum exact test

data:  inflow1 and outflow1
W = 408, p-value = 0.06495
alternative hypothesis: true location shift is not equal to 0

Error in wilcox.test.default(inflow2, outflow2, exact = FALSE) : 
  not enough (non-missing) 'x' observations
> print(test_result)# p = 0.06

	Wilcoxon rank sum exact test

data:  inflow1 and outflow1
W = 408, p-value = 0.06495
alternative hypothesis: true location shift is not equal to 0

> test_result <- wilcox.test(inflow3, outflow3, exact = FALSE) # Typically want at least 10 observations per group 
Error in wilcox.test.default(inflow3, outflow3, exact = FALSE) : 
  not enough (non-missing) 'x' observations
> print(test_result)# p = 0.06

	Wilcoxon rank sum exact test

data:  inflow1 and outflow1
W = 408, p-value = 0.06495
alternative hypothesis: true location shift is not equal to 0

I have a few problems here:

When running the Wilcoxon rank-sum test for inflow1 and outflow1, I am getting a p-value of 0.06495. I definitely expected the difference to be significant.
When running the Wilcoxin rank-sum test for inflow2 and outflow 2, I am getting the error shown below:

> test_result <- wilcox.test(inflow2, outflow2, exact = FALSE)  
Error in wilcox.test.default(inflow2, outflow2, exact = FALSE) : 
  not enough (non-missing) 'x' observations

It appears as if my error is due to having too small of a sample size (n = 25 for inflow1 and outflow1, n = 12 for inflow2 and outflow2, and n = 14 for inflow3 and outflow3). Does anyone have any advice as to how to determine:

Statistical difference between inflow1 and outflow1
Statistical difference between inflow2 and outflow2
Statistical difference between inflow3 and outflow3.

For every sample set collected the outflow concentrations were approximately half of the inflow concentrations, so I have a hard time believing that they wouldn't be statistically different. I want to be able to show the p-values for my conference poster though.

FJCC · February 22, 2025, 5:07pm

Can you post your data ? The output of

dput(inflow2)
dput(outflow2)

would allow others to replicate your test.

jrkrideau · February 22, 2025, 5:59pm

I second FJCC request but if your data is in a data.frame or tibble, it probable would be better to supply the entire dataset.

Do dput(mydata) where "mydata" is the name of your dataset. For really large datasets probably dput(head(mydata, 100)) will do. Paste the output between
```

```

Am I correct that Inflow1 and Outflow1 is the input and output from a single process?

May I ask why you are using a wilcox.test?

brant · February 22, 2025, 8:57pm

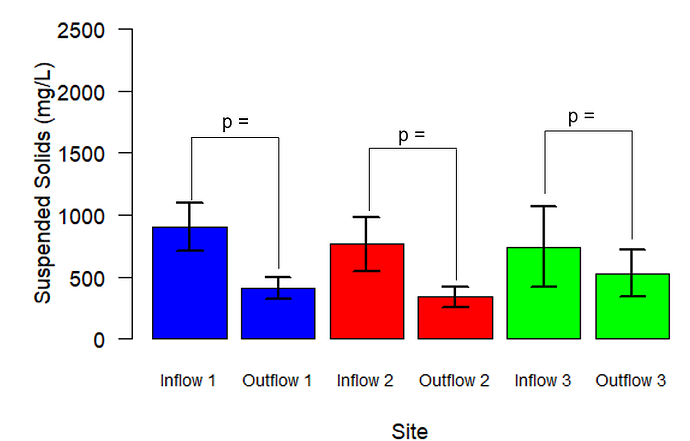
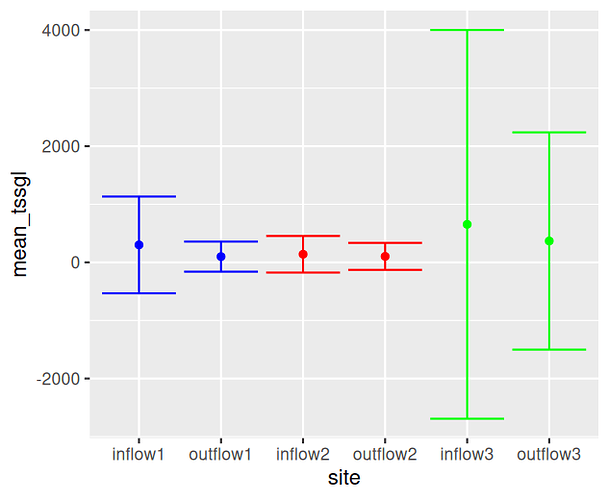
Thank you. I just posted my data below. Note that the site names in my raw data correspond to street names, and are thus different than what is shown in the graph. "Inflow 1" = "Hinton Inflow Front Cell", "Outflow 1" = "Hinton Outflow", "Inflow 2" = "Cuyler and Dewe Inflow", "Outflow 2" = "Cuyler and Dewe Outflow", "Inflow 3" = "Cuyler and Current Inflow", and "Outflow 3" = "Cuyler and Current Outflow"

dput(head(rainfall,100))
structure(list(Rainfall.Number = c(1L, 1L, 1L, 1L, 1L, 1L, 1L, 
1L, 1L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 3L, 3L, 4L, 4L, 
4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 
5L, 5L, 5L, 6L, 6L, 6L, 6L, 6L, 6L, 6L, 6L, 6L, 6L, 6L, 7L, 7L, 
7L, 7L, 7L, 7L, 7L, 8L, 8L, 8L, 8L, 8L, 8L, 8L, 8L, 8L, 8L, 8L, 
8L, 9L, 9L, 9L, 9L, 9L, 9L, 9L, 9L, 9L, 10L, 10L, 10L, 10L, 10L, 
10L, 10L, 10L, 10L, 11L, 11L, 11L, 11L, 11L, 11L, 11L, 12L, 12L, 
12L), Date = c("2022-08-05", "2022-08-05", "2022-08-05", "2022-08-05", 
"2022-08-05", "2022-08-05", "2022-08-05", "2022-08-05", "2022-08-05", 
"2022-08-18", "2022-08-18", "2022-08-18", "2022-08-18", "2022-08-18", 
"2022-08-18", "2022-08-18", "2022-08-18", "2022-08-18", "2022-08-18", 
"2022-08-23", "2022-08-23", "2022-09-09", "2022-09-09", "2022-09-09", 
"2022-09-09", "2022-09-09", "2022-09-09", "2022-09-09", "2022-09-09", 
"2022-09-09", "2022-09-09", "2022-09-09", "2022-09-25", "2022-09-25", 
"2022-09-25", "2022-09-25", "2022-09-25", "2022-09-25", "2022-09-25", 
"2022-09-25", "2022-09-25", "2022-09-25", "2022-10-12", "2022-10-12", 
"2022-10-12", "2022-10-12", "2022-10-12", "2022-10-12", "2022-10-12", 
"2022-10-12", "2022-10-12", "2022-10-12", "2022-10-12", "2022-11-06", 
"2022-11-06", "2022-11-06", "2022-11-06", "2022-11-06", "2022-11-06", 
"2022-11-06", "2023-04-29", "2023-04-29", "2023-04-29", "2023-04-29", 
"2023-04-29", "2023-04-29", "2023-04-29", "2023-04-29", "2023-04-29", 
"2023-04-29", "2023-04-29", "2023-04-29", "2023-05-19", "2023-05-19", 
"2023-05-19", "2023-05-19", "2023-05-19", "2023-05-19", "2023-05-19", 
"2023-05-19", "2023-05-19", "2023-06-24", "2023-06-24", "2023-06-24", 
"2023-06-24", "2023-06-24", "2023-06-24", "2023-06-24", "2023-06-24", 
"2023-06-24", "2023-06-29", "2023-06-29", "2023-06-29", "2023-06-29", 
"2023-06-29", "2023-06-29", "2023-06-29", "2023-07-09", "2023-07-09", 
"2023-07-09"), Site = c("Hinton Upstream", "Hinton Inflow Front Cell", 
"Hinton Outflow", "Hinton Downstream", "Blanchard Upstream", 
"Blanchard Inflow", "Blanchard Downstream", "Cuyler and Dewe Inflow", 
"Cuyler and Dewe Outflow", "Hinton Upstream", "Hinton Inflow Front Cell", 
"Hinton Inflow Back Cell", "Hinton Outflow", "Hinton Downstream", 
"Blanchard Upstream", "Blanchard Inflow", "Blanchard Downstream", 
"Cuyler and Current Inflow", "Cuyler and Current Outflow", "Cuyler and Current Inflow", 
"Cuyler and Current Outflow", "Hinton Upstream", "Hinton Inflow Front Cell", 
"Hinton Outflow", "Hinton Downstream", "Blanchard Upstream", 
"Blanchard Inflow", "Blanchard Downstream", "Cuyler and Dewe Inflow", 
"Cuyler and Dewe Outflow", "Cuyler and Current Inflow", "Cuyler and Current Outflow", 
"Hinton Upstream", "Hinton Inflow Front Cell", "Hinton Inflow Back Cell", 
"Hinton Outflow", "Hinton Downstream", "Blanchard Upstream", 
"Blanchard Inflow", "Blanchard Downstream", "Cuyler and Current Inflow", 
"Cuyler and Current Outflow", "Hinton Upstream", "Hinton Inflow Front Cell", 
"Hinton Outflow", "Hinton Downstream", "Blanchard Upstream", 
"Blanchard Inflow", "Blanchard Downstream", "Cuyler and Dewe Inflow", 
"Cuyler and Dewe Outflow", "Cuyler and Current Inflow", "Cuyler and Current Outflow", 
"Hinton Upstream", "Hinton Inflow Front Cell", "Hinton Outflow", 
"Hinton Downstream", "Blanchard Upstream", "Blanchard Inflow", 
"Blanchard Downstream", "Blanchard Upstream", "Blanchard Inflow", 
"Blanchard Downstream", "Hinton Upstream", "Hinton Inflow Front Cell", 
"Hinton Inflow Back Cell", "Hinton Outflow", "Hinton Downstream", 
"Cuyler and Dewe Inflow", "Cuyler and Dewe Outflow", "Cuyler and Current Inflow", 
"Cuyler and Current Outflow", "Blanchard Upstream", "Blanchard Inflow", 
"Blanchard Downstream", "Hinton Upstream", "Hinton Inflow Front Cell", 
"Hinton Outflow", "Hinton Downstream", "Cuyler and Current Inflow", 
"Cuyler and Current Outflow", "Blanchard Upstream", "Blanchard Inflow", 
"Blanchard Downstream", "Hinton Upstream", "Hinton Inflow Front Cell", 
"Hinton Outflow", "Hinton Downstream", "Cuyler and Dewe Inflow", 
"Cuyler and Dewe Outflow", "Blanchard Upstream", "Blanchard Inflow", 
"Blanchard Downstream", "Hinton Upstream", "Hinton Inflow Front Cell", 
"Hinton Outflow", "Hinton Downstream", "Blanchard Upstream", 
"Blanchard Inflow", "Blanchard Downstream"), pH = c(7.84, 6.24, 
7.51, 8.25, 8.07, 7.35, 8.11, 8.52, 7.85, 8.01, 7.76, 7.08, 7.51, 
8.23, 7.77, 7.09, 7.78, 7.32, 7.04, 6.98, 7.22, 8.27, 7.71, 6.99, 
7.88, 8.09, 7.39, 7.96, 8.79, 7.58, 7.22, 6.95, 7.81, 7.41, 7.7, 
7.81, 7.68, 7.88, 7.25, 7.82, 7.31, 6.92, 8.05, 6.93, 7.96, 8.03, 
8, 7.31, 7.66, 8.05, 7.65, 7.25, 7, 7.9, 6.68, 6.78, 7.86, 8.09, 
6.69, 7.85, 7.64, 7.86, 7.57, 7.48, 7.82, 7.72, 7.4, 7.74, 8.04, 
7.58, 7.96, 7.72, 7.73, 7.27, 7.56, 7.68, 6.41, 7.1, 7.78, 6.96, 
6.65, 7.6, 6.67, 7.99, 7.88, 5.3, 6.97, 7.67, 7.62, 7.37, 7.72, 
6.53, 8.03, 8.04, 6.88, 7.06, 8.04, 7.96, 6.07, 7.66), TDS = c(224L, 
39L, 165L, 230L, 231L, 25L, 250L, 45L, 42L, 269L, 20L, 44L, 223L, 
254L, 170L, 48L, 155L, 20L, 191L, 35L, 188L, 379L, 66L, 99L, 
283L, 312L, 62L, 271L, 44L, 47L, 13L, 87L, 219L, 16L, 228L, 204L, 
213L, 218L, 19L, 231L, 22L, 197L, 282L, 53L, 193L, 277L, 246L, 
27L, 241L, 59L, 61L, 24L, 175L, 210L, 47L, 102L, 201L, 232L, 
36L, 211L, 209L, 47L, 182L, 191L, 65L, 166L, 273L, 180L, 50L, 
199L, 39L, 49L, 148L, 63L, 153L, 140L, 137L, 159L, 147L, 33L, 
410L, 251L, 35L, 268L, 255L, 127L, 150L, 255L, 77L, 150L, 245L, 
39L, 243L, 461L, 82L, 140L, 238L, 293L, 47L, 249L), Ec = c(447L, 
78L, 330L, 460L, 463L, 51L, 500L, 90L, 85L, 536L, 41L, 88L, 446L, 
510L, 340L, 96L, 310L, 40L, 382L, 71L, 377L, 782L, 133L, 199L, 
567L, 625L, 124L, 540L, 88L, 93L, 26L, 175L, 438L, 32L, 456L, 
408L, 426L, 436L, 38L, 462L, 44L, 395L, 568L, 106L, 386L, 554L, 
492L, 55L, 481L, 118L, 123L, 47L, 350L, 421L, 95L, 204L, 401L, 
512L, 72L, 422L, 417L, 95L, 364L, 383L, 131L, 338L, 545L, 360L, 
99L, 398L, 77L, 100L, 297L, 125L, 308L, 281L, 279L, 318L, 293L, 
66L, 819L, 501L, 70L, 536L, 510L, 254L, 300L, 511L, 154L, 301L, 
490L, 77L, 487L, 231L, 164L, 280L, 475L, 586L, 95L, 497L), Turbidity..NTU. = c(1.64, 
7.25, 5.63, 2.06, 3.08, 5.62, 3.29, 11.1, 3.95, 7.15, 12.9, 7.71, 
7.5, 7.1, 21.4, 12.5, 19.6, 3.84, 3.11, 81.7, 20.6, 5.9, 47.2, 
63.8, 7.44, 2.92, 9.21, 2.21, 7.31, 6.12, 29.3, 11.6, 6.9, 4.8, 
7, 7.11, 9.26, 3.93, 7.28, 4.01, 8.11, 3.59, 6.64, 7.12, 0.25, 
5.32, 2.43, 12.5, 6.25, 28.1, 4.95, 4.32, 8.78, 6.42, 27.1, 24.8, 
7.21, 3.99, 12.2, 0.7, 16.1, 37, 14, 8.56, 60.6, 7.41, 16.5, 
13.2, 98, 43.8, 31.6, 9.42, 12.1, 60.4, 14.9, 34.2, 94, 66.4, 
22.1, 55.5, 6.55, 34.4, 4.87, 16.4, 4.07, 644, 25.9, 4.69, 32.9, 
27.8, 52.8, 37.9, 53.5, 17.8, 91.7, 26.1, 63, 36.2, 30, 9.07), 
    TSS..g.L. = c(NA, NA, NA, NA, NA, NA, NA, NA, NA, 8.408, 
    8.794, 8.794, 8.898, 8.97, 9.67, 8.646, 4.32, 8.52, 8.96, 
    9.1, 8.85, 8.92, 9.38, 8.9, 8.27, 8.19, 8.59, 8.4, 8.64, 
    8.5, 8.5, 4.23, 8.59, 8.86, 8.66, 7.98, 8.2, 8.67, 8.55, 
    8.68, 4.21, 4.48, 4.193, 4.866, 4.28, 4.44, 4.29, 4.24, 4.57, 
    4.38, 4.21, 4.46, 4.54, 6.2, 5.124, 4.88, 6, 6, 7.2, 6.02, 
    123, 105, 95, 109, 250, 70.59, 91.95, 117.65, 313.87, 237.7, 
    98.16, 57.43, 66.797, 248.7, 47.964, 73.333, 484.63, 197.909, 
    851.33, 4449.04, 2487.91, 127.17, 431.37, 241.76, 177.78, 
    1107.53, 196.26, 172.73, 233.01, 162.16, 282.21, 482.35, 
    401.96, 120.97, 821.92, 367.92, 2365.52, 192.1, 299.1, 82
    ), DOC..mg.L. = c(NA, NA, NA, NA, NA, NA, NA, NA, NA, 16.65, 
    10.65, 14.73, 14.23, 16.05, 9.114, 21.52, 11.7, 25.6, 16.19, 
    18.37, 10.04, 11.52, 14.8, 20.12, 18, 12.27, 23.27, 15.02, 
    25.01, 27.82, 14.2, 9.55, 17.88, 8.045, 16.73, 14.78, 18.15, 
    18.34, 10.75, 17.67, 13.8, 9.05, 14.97, 23.41, 7.97, 12.75, 
    12.45, 11.86, 12.63, 7.92, 10.61, 15.7, 7.9, 13.57, 17.73, 
    19.35, 14.36, 13.08, 28.47, 13.83, 14.95, 13.49, 14.44, 15.2, 
    17.3, 9.759, 12.16, 14.71, 8.33, 10.02, 10.25, 7.567, 15.89, 
    31.11, 17.56, 15.45, 17.45, 16.01, 15.73, 24.65, 9.027, 18.34, 
    26.98, 17.87, 11.88, 16.56, 31.58, 11.81, 15.9, 18.9, 15.79, 
    21.12, 12.01, 12.1, 16.35, 13.73, 14.11, 15.88, 29.54, 14.21
    ), Ammonia = c("0.78", "4.32", "0.54", "0.78", "0.43", "1.3", 
    "0.23", "0.24", "0.36", "0.92", "0.43", "0.6", "0.48", "0.31", 
    "1.8", "3.44", "2.11", "0.34", "0.3", "0.78", "0.23", "2.52", 
    "1.24", "1.74", "0.48", "0.35", "0.54", "0.43", "3.36", "0.31", 
    "0.47", "0.21", "0.35", "0.47", "0.13", "0.56", "0.28", "0.44", 
    "0.47", "0.39", "0.24", "0.2", "1.42", "0.69", "0.39", "1.49", 
    "0.36", "1.06", "0.84", "1.58", "0.73", "1.3", "0.78", "1.88", 
    "0.91", "0.32", "1.42", "0.64", "0.37", "0.48", "0.74", "1.76", 
    "0.29", "0.27", "3", "7.84", "0.68", "0.18", "0.77", "0.54", 
    "0.85", "1", "1.82", "0.54", "0.18", "0.67", "0.76", "0.66", 
    "0.89", "1.02", "0.57", "0.95", "0.79", "0.96", "0.37", "0.85", 
    "0.52", "0.37", "0.64", "0.79", "0.82", "0.96", "2", "0.29", 
    "1.42", "0.26", "0.65", "1.34", "1.5", "1.32"), Nitrate = c(0.172, 
    0.161, 0.155, 0.434, 0.405, 0.124, 0.399, 0.131, 0.178, 1.01, 
    0.138, 0.845, 0.5, 0.6, 0.25, 0.214, 0.403, 0.15, 0.72, 0.54, 
    0.61, 0.341, 0.44, 0.329, 0.99, 1.01, 1.327, 1.29, 0.985, 
    1.67, 0.03, 0.276, 0.15, 0.308, 0.605, 0.299, 0.337, 0.755, 
    0.144, 0.532, 0.091, 0.135, 0.301, 0.052, 0.194, 0.227, 0.388, 
    0.291, 0.239, 0.132, 0.484, 0.164, 0.139, 0.349, 0.379, 0.094, 
    0.281, 0.885, 0.077, 0.069, 0.51, 0.062, 0.227, 0.254, 0.001, 
    0.246, 0.095, 0.34, 0, 0.028, 0.13, 0.299, 0.304, 0.015, 
    0.171, 0.198, 0.349, 0.222, 0.195, 0.185, 0.379, 0.161, 0.165, 
    0.161, 0.293, 0.68, 0.125, 0.066, 0.149, 0.77, 0.319, 0.141, 
    0.255, 0.178, 0.54, 0.12, 0.177, 0.229, 0.073, 0.228), Nitrite = c(0.004, 
    0.03, 0.013, 0.029, 0.007, 0.016, 0.007, 0.007, 0.009, 0.004, 
    0.006, 0.005, 0.055, 0.059, 0.009, 0.024, 0.001, 0.007, 0.004, 
    0.01, 0.01, 0.035, 0.01, 0.066, 0.021, 0.016, 0.015, 0.02, 
    0.042, 0.011, 0.008, 0.008, 0.018, 0.009, 0.03, 0.008, 0.012, 
    0.029, 0.008, 0.037, 0.013, 0.008, 0.01, 0.001, 0.019, 0.016, 
    0.008, 0.021, 0.006, 0.017, 0.017, 0.016, 0.015, 0.006, 0.001, 
    0.001, 0.007, 0.006, 0.003, 0.002, 0.008, 0.001, 0.008, 0.064, 
    0.001, 0.009, 0.001, 0.01, 0, 0, 0.002, 0.007, 0.008, 0.05, 
    0.032, 0.008, 0.027, 0.009, 0.019, 0.008, 0.008, 0.012, 0.027, 
    0.041, 0.047, 0.036, 0.033, 0.019, 0.04, 0.019, 0.016, 0.004, 
    0.042, 0.014, 0.84, 0.019, 0.028, 0.015, 0.001, 0.015), Phosphate = c(0.14, 
    0.23, 0.11, 0.13, 0.01, 0.14, 0.01, 0.15, 0.16, 0.01, 0.22, 
    0.29, 0.54, 0.16, 0.36, 0.18, 0.39, 0.16, 0.15, 0.81, 1.76, 
    0.17, 0.47, 0.53, 0.17, 0.79, 0.93, 0.48, 0.34, 0.63, 0.29, 
    0.22, 0.17, 0.06, 0.11, 0.13, 0.15, 0.13, 0.01, 0.13, 0.19, 
    0.31, 0.01, 0.18, 0.32, 0.19, 0.12, 0.29, 0.15, 0.3, 0.91, 
    0.18, 0.72, 0.18, 0.16, 0.22, 0.13, 0.1, 0.77, 0.15, 0.04, 
    0.1, 0.06, 0.16, 0.05, 0.38, 0.42, 0.35, 0.43, 0.21, 0.51, 
    0.38, 0.26, 0.18, 0.22, 0.13, 0.32, 0.22, 0.11, 0.27, 0.01, 
    0.17, 0.01, 0.01, 0.07, 0.32, 0.24, 0.63, 0.25, 3.5, 0.36, 
    0.84, 0.2, 0.1, 2.2, 0.26, 0.67, 0.33, 0, 0.32), Zinc = c(0.67, 
    0.82, 0.33, 0.08, 0.35, 0.29, 0.03, 0.09, 0.1, 1.62, 0.24, 
    0.05, 0.21, 0.59, 0.28, 0.08, 3.92, 0.63, 1.21, 0.04, 0.26, 
    0.97, 0.11, 0.13, 0.47, 0.18, 0.63, 0.63, 0.33, 0.25, 0.2, 
    0.23, 0.38, 0.17, 0.11, 0.32, 0.23, 0.19, 0.15, 0.27, 0.55, 
    0.3, 2.44, 0.31, 0.16, 2.13, 1.02, 0.14, 1.06, 0.15, 1.05, 
    0.3, 0.21, 0.15, 0.13, 0.26, 0.14, 0.56, 0.4, 0.46, 0.18, 
    0.4, 0.26, 0.45, 0.01, 0.29, 0.22, 0.45, 0.25, 0.63, 0.26, 
    0.13, 0.19, 0.7, 0.76, 0.09, 0.73, 0.22, 0.13, 0.23, 0.21, 
    0.01, 0.04, 0.01, 0.01, 1.27, 0.05, 0.01, 1.01, 0.17, 1.14, 
    1.09, 0.4, 0.61, 1.72, 0.74, 0.56, 0.6, 0.04, 0.6), Iron = c(0.17, 
    0.14, 0.09, 0.12, 0.28, 0.06, 0.32, 0.04, 0.17, 0.1, 0.05, 
    0.04, 0.17, 0.14, 0.17, 0.01, 0.11, 0.06, 0.18, 0.01, 0.17, 
    0.11, 0.25, 0.53, 0.12, 0.15, 0.33, 0.23, 0.14, 0.07, 0.07, 
    0.01, 0.13, 0.04, 0.07, 0.07, 0.21, 0.27, 0.14, 0.15, 0.11, 
    0.05, 0.08, 1, 0.06, 0.53, 0.1, 0.04, 0.09, 0.07, 0.21, 0.04, 
    0.03, 0.28, 0.28, 0.37, 0.25, 0.24, 0.05, 0.11, 0.09, 0.31, 
    0.06, 0.22, 0.16, 0.08, 0.07, 0.42, 0.11, 0.01, 0.28, 0.01, 
    0.11, 0.27, 0.08, 0.06, 0.17, 0.14, 0.17, 0.01, 0.02, 0.01, 
    0.01, 0.01, 0.01, 0.37, 0.24, 0.01, 0.28, 0.06, 0.22, 0.12, 
    0.09, 0.11, 0.28, 0.21, 0.09, 0.19, 0.04, 0.18), Chloride = c(16, 
    14, 3.4, 7.4, 11.5, 0, 8.3, 2.7, 22, 16, 30, 21, 8.4, 16, 
    15.5, 14, 16, 8, 15, 9.3, 19.5, 13, 11.5, 11.5, 17.5, 10.5, 
    4.7, 16, 13, 1.4, 29, 18, 9.1, 21, 4.9, 25, 5.7, 5.9, 10, 
    6.2, 17.5, 7.2, 34, 0.01, 7.7, 14, 6.9, 2, 11, 13.5, 10.5, 
    25, 18, 5.6, 11, 3.3, 5.7, 6.3, 5.3, 8.2, 21, 11.5, 23, 7.8, 
    0.7, 4.7, 21.5, 8.2, 0.01, 10.5, 15, 21, 20.5, 4.4, 4.5, 
    3.3, 0.01, 6.2, 3.4, 10, 18, 0.5, 0, 5, 2.8, 0, 3.2, 3.7, 
    0, 0, 13.5, 10.5, 9.2, 15, 18.5, 12.5, 11.5, 11, 12.5, 11
    )), row.names = c(NA, 100L), class = "data.frame")

brant · February 22, 2025, 9:06pm

@jrkrideau Yes, Inflow1 and Outflow 1 are the input and output from a single process, Inflow 2 and Outflow 2 are the input and output from another process, and Inflow 3 and Outflow 3 are the input and output from a third process. I was using a wilcox.test because my sample size is relatively small (n = 25 for Inflow 1 and Outflow 1, n = 12 for Inflow 2 and Outflow 2, and n = 14 for Inflow 3 and Outflow 3). It is expected that for each process, the outflow concentrations will be lower than the inflow concentrations, but I want to test the statistical significance of this. I am open to any suggestions if there is a better way to do this than a wilcox.test. It doesn't make much difference to me as long as i can accurately test statistical differences between sites and assign a p-value to my graph.

brant · February 22, 2025, 9:21pm

I am ultimately trying to add p-values to the graph below for one of my conference presentations next month. I am open to any suggestions on tests to use as long as they will help me test for statistical difference between these bars.

FJCC · February 22, 2025, 9:55pm

Thanks for posting the data. I'm confused by it. I loaded it into a data frame named DF and used table() to count the occurrences of each Site.

 table(DF$Site)

      Blanchard Downstream           Blanchard Inflow         Blanchard Upstream  Cuyler and Current Inflow 
                        11                         11                         11                          7 
Cuyler and Current Outflow     Cuyler and Dewe Inflow    Cuyler and Dewe Outflow          Hinton Downstream 
                         7                          5                          5                         10 
   Hinton Inflow Back Cell   Hinton Inflow Front Cell             Hinton Outflow            Hinton Upstream 
                         3                         10                         10                         10

The sites you list have 10, 5 and 7 samples, not 25, 12, and 14. Also, it is not clear which column you have plotted. Since your plot labels the y axis Suspended Solids, I guess TSS..g.L, but summarizing that column by Site gives values very different from you plot.

  Site        Avg
  <chr>     <dbl>
1 Inflow 1  300. 
2 Inflow 2  140. 
3 Inflow 3  655. 
4 Outflow 1  98.8
5 Outflow 2 103. 
6 Outflow 3 368.

Please explain how your data maps to your plot and quoted sample numbers.

brant · February 22, 2025, 10:25pm

@FJCC. Sorry for the confusion. Posit would not allow me to upload all of the occurrences due to character restrictions on this forum. My full data has samples sizes of 25, 12 and 14, but in my dput() function I only included the first 100 records as I have a fairly large dataset. It appears that the first 100 records provides 10, 5, and 7 samples, while my full dataset has 25, 12, and 14 samples. Posit only allows us to pose up to 32000 characters in this forum. My full dataset has 32184 characters.

Likewise the first 100 records is only a small snapshot of my data and does not capture seasonality (i.e., suspended concentrations are higher in spring, and my dput() data provided fall data). This is likely why you have very different values than what I plotted.

In terms of how my data maps to my plot:

Hinton Inflow Front Cell = Inflow 1
Hinton Outflow = Outflow 1
Cuyler and Dewe Inflow = Inflow 2
Cuyler and Dewe Outflow = Outflow 2
Cuyler and Current Inflow = Inflow 3
Cuyler and Current Outflow = Outflow 3

I am plotting the column TSS..g.L. Sorry for the confusion.

FJCC · February 23, 2025, 5:51am

Here is an example of running the wilcox.test() on your suspended solid values without getting an error. I deleted the unnecessary columns from your data frame to simplify the example.

library(tidyverse)
DF <- structure(list(Rainfall.Number = c(1L, 1L, 1L, 1L, 1L, 1L, 1L, 
                                         1L, 1L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 3L, 3L, 4L, 4L, 
                                         4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 
                                         5L, 5L, 5L, 6L, 6L, 6L, 6L, 6L, 6L, 6L, 6L, 6L, 6L, 6L, 7L, 7L, 
                                         7L, 7L, 7L, 7L, 7L, 8L, 8L, 8L, 8L, 8L, 8L, 8L, 8L, 8L, 8L, 8L, 
                                         8L, 9L, 9L, 9L, 9L, 9L, 9L, 9L, 9L, 9L, 10L, 10L, 10L, 10L, 10L, 
                                         10L, 10L, 10L, 10L, 11L, 11L, 11L, 11L, 11L, 11L, 11L, 12L, 12L, 
                                         12L), Date = c("2022-08-05", "2022-08-05", "2022-08-05", "2022-08-05", 
                                                        "2022-08-05", "2022-08-05", "2022-08-05", "2022-08-05", "2022-08-05", 
                                                        "2022-08-18", "2022-08-18", "2022-08-18", "2022-08-18", "2022-08-18", 
                                                        "2022-08-18", "2022-08-18", "2022-08-18", "2022-08-18", "2022-08-18", 
                                                        "2022-08-23", "2022-08-23", "2022-09-09", "2022-09-09", "2022-09-09", 
                                                        "2022-09-09", "2022-09-09", "2022-09-09", "2022-09-09", "2022-09-09", 
                                                        "2022-09-09", "2022-09-09", "2022-09-09", "2022-09-25", "2022-09-25", 
                                                        "2022-09-25", "2022-09-25", "2022-09-25", "2022-09-25", "2022-09-25", 
                                                        "2022-09-25", "2022-09-25", "2022-09-25", "2022-10-12", "2022-10-12", 
                                                        "2022-10-12", "2022-10-12", "2022-10-12", "2022-10-12", "2022-10-12", 
                                                        "2022-10-12", "2022-10-12", "2022-10-12", "2022-10-12", "2022-11-06", 
                                                        "2022-11-06", "2022-11-06", "2022-11-06", "2022-11-06", "2022-11-06", 
                                                        "2022-11-06", "2023-04-29", "2023-04-29", "2023-04-29", "2023-04-29", 
                                                        "2023-04-29", "2023-04-29", "2023-04-29", "2023-04-29", "2023-04-29", 
                                                        "2023-04-29", "2023-04-29", "2023-04-29", "2023-05-19", "2023-05-19", 
                                                        "2023-05-19", "2023-05-19", "2023-05-19", "2023-05-19", "2023-05-19", 
                                                        "2023-05-19", "2023-05-19", "2023-06-24", "2023-06-24", "2023-06-24", 
                                                        "2023-06-24", "2023-06-24", "2023-06-24", "2023-06-24", "2023-06-24", 
                                                        "2023-06-24", "2023-06-29", "2023-06-29", "2023-06-29", "2023-06-29", 
                                                        "2023-06-29", "2023-06-29", "2023-06-29", "2023-07-09", "2023-07-09", 
                                                        "2023-07-09"), 
                     Site = c("Hinton Upstream", "Hinton Inflow Front Cell", 
                              "Hinton Outflow", "Hinton Downstream", "Blanchard Upstream", 
                              "Blanchard Inflow", "Blanchard Downstream", "Cuyler and Dewe Inflow", 
                              "Cuyler and Dewe Outflow", "Hinton Upstream", "Hinton Inflow Front Cell", 
                              "Hinton Inflow Back Cell", "Hinton Outflow", "Hinton Downstream", 
                              "Blanchard Upstream", "Blanchard Inflow", "Blanchard Downstream", 
                              "Cuyler and Current Inflow", "Cuyler and Current Outflow", "Cuyler and Current Inflow", 
                              "Cuyler and Current Outflow", "Hinton Upstream", "Hinton Inflow Front Cell", 
                              "Hinton Outflow", "Hinton Downstream", "Blanchard Upstream", 
                              "Blanchard Inflow", "Blanchard Downstream", "Cuyler and Dewe Inflow", 
                              "Cuyler and Dewe Outflow", "Cuyler and Current Inflow", "Cuyler and Current Outflow", 
                              "Hinton Upstream", "Hinton Inflow Front Cell", "Hinton Inflow Back Cell", 
                              "Hinton Outflow", "Hinton Downstream", "Blanchard Upstream", 
                              "Blanchard Inflow", "Blanchard Downstream", "Cuyler and Current Inflow", 
                              "Cuyler and Current Outflow", "Hinton Upstream", "Hinton Inflow Front Cell", 
                              "Hinton Outflow", "Hinton Downstream", "Blanchard Upstream", 
                              "Blanchard Inflow", "Blanchard Downstream", "Cuyler and Dewe Inflow", 
                              "Cuyler and Dewe Outflow", "Cuyler and Current Inflow", "Cuyler and Current Outflow", 
                              "Hinton Upstream", "Hinton Inflow Front Cell", "Hinton Outflow", 
                              "Hinton Downstream", "Blanchard Upstream", "Blanchard Inflow", 
                              "Blanchard Downstream", "Blanchard Upstream", "Blanchard Inflow", 
                              "Blanchard Downstream", "Hinton Upstream", "Hinton Inflow Front Cell", 
                              "Hinton Inflow Back Cell", "Hinton Outflow", "Hinton Downstream", 
                              "Cuyler and Dewe Inflow", "Cuyler and Dewe Outflow", "Cuyler and Current Inflow", 
                              "Cuyler and Current Outflow", "Blanchard Upstream", "Blanchard Inflow", 
                              "Blanchard Downstream", "Hinton Upstream", "Hinton Inflow Front Cell", 
                              "Hinton Outflow", "Hinton Downstream", "Cuyler and Current Inflow", 
                              "Cuyler and Current Outflow", "Blanchard Upstream", "Blanchard Inflow", 
                              "Blanchard Downstream", "Hinton Upstream", "Hinton Inflow Front Cell", 
                              "Hinton Outflow", "Hinton Downstream", "Cuyler and Dewe Inflow", 
                              "Cuyler and Dewe Outflow", "Blanchard Upstream", "Blanchard Inflow", 
                              "Blanchard Downstream", "Hinton Upstream", "Hinton Inflow Front Cell", 
                              "Hinton Outflow", "Hinton Downstream", "Blanchard Upstream", 
                              "Blanchard Inflow", "Blanchard Downstream"), 
                     TSS..g.L. = c(NA, NA, NA, NA, NA, NA, NA, NA, NA, 8.408, 
                                   8.794, 8.794, 8.898, 8.97, 9.67, 8.646, 4.32, 8.52, 8.96, 
                                   9.1, 8.85, 8.92, 9.38, 8.9, 8.27, 8.19, 8.59, 8.4, 8.64, 
                                   8.5, 8.5, 4.23, 8.59, 8.86, 8.66, 7.98, 8.2, 8.67, 8.55, 
                                   8.68, 4.21, 4.48, 4.193, 4.866, 4.28, 4.44, 4.29, 4.24, 4.57, 
                                   4.38, 4.21, 4.46, 4.54, 6.2, 5.124, 4.88, 6, 6, 7.2, 6.02, 
                                   123, 105, 95, 109, 250, 70.59, 91.95, 117.65, 313.87, 237.7, 
                                   98.16, 57.43, 66.797, 248.7, 47.964, 73.333, 484.63, 197.909, 
                                   851.33, 4449.04, 2487.91, 127.17, 431.37, 241.76, 177.78, 
                                   1107.53, 196.26, 172.73, 233.01, 162.16, 282.21, 482.35, 
                                   401.96, 120.97, 821.92, 367.92, 2365.52, 192.1, 299.1, 82
                     )), row.names = c(NA, 100L), class = "data.frame")




DFnew <- DF |> mutate(Site = case_when(
Site ==  'Hinton Inflow Front Cell' ~ 'Inflow_1',
Site == 'Hinton Outflow' ~ 'Outflow_1',
Site == 'Cuyler and Dewe Inflow' ~ 'Inflow_2',
Site == 'Cuyler and Dewe Outflow' ~ 'Outflow_2',
Site == 'Cuyler and Current Inflow' ~ 'Inflow_3',
Site == 'Cuyler and Current Outflow' ~ 'Outflow_3',
TRUE ~ 'Not Appl'
)) |> filter(Site != 'Not Appl') |> 
  select(Rainfall.Number, Site, TSS..g.L.) |> 
  pivot_wider(names_from = Site, values_from = 'TSS..g.L.')

wilcox.test(DFnew$Inflow_1, DFnew$Outflow_1, data = tmp)
#> 
#>  Wilcoxon rank sum exact test
#> 
#> data:  DFnew$Inflow_1 and DFnew$Outflow_1
#> W = 49, p-value = 0.4894
#> alternative hypothesis: true location shift is not equal to 0
wilcox.test(DFnew$Inflow_2, DFnew$Outflow_2, data = tmp)
#> 
#>  Wilcoxon rank sum exact test
#> 
#> data:  DFnew$Inflow_2 and DFnew$Outflow_2
#> W = 10, p-value = 0.6857
#> alternative hypothesis: true location shift is not equal to 0
wilcox.test(DFnew$Inflow_3, DFnew$Outflow_3, data = tmp)
#> 
#>  Wilcoxon rank sum exact test
#> 
#> data:  DFnew$Inflow_3 and DFnew$Outflow_3
#> W = 25, p-value = 1
#> alternative hypothesis: true location shift is not equal to 0

^{Created on 2025-02-22 with reprex v2.1.1}

Here are some unsolicted comments on your data.
I see very large variation in DFnew() of the values of TSS..g.L. I don't know how you got the error bars on your plot, but they look too small.
The relationship between the inflow and outflow TSS seems to depend on the size of the inflow. High flows show a large differences but low flows do not.
It may make sense to treat the data as paired values since each inflow and outflow is related to a Rainfall event.
Don't have spaces in your variable names. It makes life needlessly difficult. Notice I changed Inflow 1 to Inflow_1, etc.