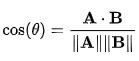Cosine similarity between columns of two sparse matrices

[kongcav]

Hi Posit Community,

I have two matrices of Z-scores (differential gene expression). They have variables (genes) as rows, samples (observations) as columns:
Query: 1000 rows x 2000 samples
Reference: 1000 rows x 720000 samples
They are sparse as they have been filtered on significance of the Z-scores, setting all values below the threshold to zero.

The overall goal is to calculate cosine similarities between each sample (column) across the two matrices (Query_I to Reference_J) resulting in a 2000 x 720000 matrix, then scaling the cosine similarities based on the number of non-zero overlaps between the i,j samples (as a measure of support for each similarity), turning that into a distance measure and then finally do hierarchical clustering (complete linkage) using these distances.

I am working in an HPC environment where I'm capped at 350GB memory, 32 CPU cores. I have access to GPU clusters as well if necessary.

library(Matrix)

# Simulate some (100x smaller) data
q_mat <- Matrix(data = rnorm(n = 2e4, mean = 0, sd = 0.9, nrow = 1000)
r_mat <- Matrix(data = rnorm(n = 7.2e6, mean = 0, sd = 0.9, nrow = 1000)

# Filter Z-scores on significance level
threshold <- 2
q_mat[abs(q_mat) < threshold] <- 0
r_mat[abs(r_mat) < threshold] <- 0

# Drop samples that do not contain atleast 1 significant value
q_mat <- q_mat[,colSums(abs(q_mat)) != 0]
r_mat <- r_mat[,colSums(abs(r_mat)) != 0]

# My matrices have become sparse: Approximately 98% of values are zero. 
q_mat <- as(q_mat, "dgCMatrix")
r_mat <- as(r_mat, "dgCMatrix")

# Cosine similarities can easily be found with
cosine_mat <- qlcMatrix::cosSparse(q_mat, r_mat)

# Boolean matrices which tells us where each matrix is non-zero
q_idx <- q_mat != 0
r_idx <- r_mat != 0

# Getting number of overlaps
n_overlaps <- t(q_idx) %*% r_idx

# Scale the cosines by log2 of the number of overlaps
scaling_factor <- log2(n_overlaps+1)
scaled_cosines <- cosine_mat * scaling_factor

# Turn the cosines into a distance measure
distances <- max(scaled_cosines) - scaled_cosines

# Now turn this into a dist() object somehow for hclust() to use.

First question:
The cosine similarities above will have no contributions from genes where both samples are zero, but it will have contributions from genes where one of the samples is zero and the other is not. As a zero here can both mean below detection limit or truly zero but I have no way of knowing which, they need to be left out from my cosine calculation. In this way, I base the similarity only on genes which are differentially expressed in both.

# The code above will calculate the cosine similarity in the following way:
v1 <- c(0, -3, 0, 0, 5, 3, 4, 0)
v2 <- c(0, 2, 5, 0, 0, -2, 2, 3)
cosine <- v1 %*% v2 / (sqrt(sum(v1^2)) * sqrt(sum(v2^2)))

# What I want is to calculate cosines only from values where both vectors are non-zero:
idx <- v1 != 0 & v2 != 0
v1_nz <- v1[idx]
v2_nz <- v2[idx]
cosine2 <- v1_nz %*% v2_nz / (sqrt(sum(v1_nz^2)) * sqrt(sum(v2_nz^2)))

However, this filtering needs to be done based on overlaps between each set of samples compared. To my understanding, since my matrices are large (and this will be reused for many different query and reference matrices of similarly large sizes) I will want to avoid loops / apply() for subsetting genes and then calculating cosines.

Idea 1: Use Kronecker product to get a boolean matrix for filtering all combinations

kron_qr <- q_idx %x% r_idx

Output would be a sparse matrix along the lines of:

	sampleQ_1:sampleR_1	sampleQ_1:sampleR_2	...	sampleQ_2000:sampleR_720000
gene1:gene1	0	1	...	0
gene1:gene2	0	0	...	0
...	...	...	...	...
gene1000:gene1000	1	0	...	0

If I'm not entirely wrong this would take up an unfeasible amount of memory. Estimates:

# Dense (float precision):
1000*1000*2000*720000*8 / 2^30 # 10728836 GB
# Sparse (float precision):
(1000*1000*2000*720000*8 / 2^30) * 0.02 # 214577 GB

And that is ignoring any overhead.
However, I am not interested in the rows comparing expression of dissimilar genes (rows), meaning that I wasted computation time and memory on them. Is there any linear algebra voodoo I could invoke to instead get a dim 1000 x (2000*720000) matrix out instead? That would reduce the estimated size for the sparse matrix to ~215GB which may fit in memory, provided there is not too much other overhead.

Idea 2: Tensor
The above could perhaps be translated into a sparse-tensor framework using library(tensorr).
For my final cosine matrix of dim 2000 x 720000 the values each have to be calculated from two vectors of length 1000 containing 1-1000 non-zero values.
Maybe I can create a rank 3 tensor (i,j,k)=(2000 x 720000 x 1000) where the 1000-dimensional part is a boolean vector of "sampleQ_i != 0 & sampleR_j != 0". This boolean vector could then be used to subset the two vectors on which I base the i,j-th cosine similarity.

Second question:
It seems to me that due to the sizes of the matrices in question, the above methods are problematic even if I can request access to more memory. Maybe I am overcomplicating it?
Is my best bet then to do some sort of parallelized apply() ? I'm a bit worried about the runtime, and have not used parallelization approaches with R before. How would I approach this?

Sorry for the long post, and thank you for your time!

[technocrat]

@kongcav

# Now turn this into a dist() object somehow for hclust() to use.

Let's start here, since there's a lot to unpack and I'll need help clearly to understand the what of the goal.

What am I missing about using distances for hclust()

In the reprex below, I corrected syntax for q_mat/r_mat to provide interior closing ) for rnorm and updated dgCmatrix. The end result looks to be production of an hclust object that works as a formal matter, but I'm unsure if that is actually what you are looking for.

library(Matrix)

# Simulate some (100x smaller) data
q_mat <- Matrix(data = rnorm(n =   2e4, mean = 0, sd = 0.9), nrow = 1000)
r_mat <- Matrix(data = rnorm(n = 7.2e6, mean = 0, sd = 0.9), nrow = 1000)
# Filter Z-scores on significance level
threshold <- 2
q_mat[abs(q_mat) < threshold] <- 0
r_mat[abs(r_mat) < threshold] <- 0

# Drop samples that do not contain at least 1 significant value
q_mat <- q_mat[,colSums(abs(q_mat)) != 0]
r_mat <- r_mat[,colSums(abs(r_mat)) != 0]

# My matrices have become sparse: Approximately 98% of values are zero. 
q_mat <- as(q_mat, "CsparseMatrix")
r_mat <- as(r_mat, "CsparseMatrix")

# Cosine similarities can easily be found with
cosine_mat <- qlcMatrix::cosSparse(q_mat, r_mat)

# Boolean matrices which tells us where each matrix is non-zero
q_idx <- q_mat != 0
r_idx <- r_mat != 0

# Getting number of overlaps
n_overlaps <- t(q_idx) %*% r_idx

# Scale the cosines by log2 of the number of overlaps
scaling_factor <- log2(n_overlaps+1)
scaled_cosines <- cosine_mat * scaling_factor

# Turn the cosines into a distance measure
distances <- max(scaled_cosines) - scaled_cosines

# note that distances is an S4 object with values as slot @x
str(distances)
#> Formal class 'dgeMatrix' [package "Matrix"] with 4 slots
#>   ..@ Dim     : int [1:2] 20 7200
#>   ..@ Dimnames:List of 2
#>   .. ..$ : NULL
#>   .. ..$ : NULL
#>   ..@ x       : num [1:144000] 0.437 0.469 0.437 0.389 0.463 ...
#>   ..@ factors : list()

plot(hclust(dist(distances)))

^{Created on 2023-03-16 with reprex v2.0.2}

[kongcav]

Thank you very much for your answer. I'm sorry if I was not quite clear, I will try to clarify.

library(Matrix)
set.seed(30)

# Simulate some data
q_mat <- Matrix(data = rnorm(n = 30, 
                             mean = 0, 
                             sd = 2), 
                nrow = 5)
r_mat <- Matrix(data = rnorm(n = 50, 
                             mean = 0, 
                             sd = 2), 
                nrow = 5)
               
# Filter Z-scores on significance level
threshold <- 2
q_mat[abs(q_mat) < threshold] <- 0
r_mat[abs(r_mat) < threshold] <- 0

# Drop samples that do not contain atleast 1 significant value
q_mat <- q_mat[,colSums(abs(q_mat)) != 0]
r_mat <- r_mat[,colSums(abs(r_mat)) != 0]

# Most of the values are 0 after the thresholding, so they are best stored as sparse matrices:
q_mat <- as(q_mat, "dgCMatrix")
r_mat <- as(r_mat, "dgCMatrix")

I want to find the cosine similarity between each sample (column) of my query data q_mat against each sample (column) my reference data r_mat:

All values are between -1 and 1. The cosine similarity is based on the angle between vectors: When the vectors are pointed in the exact same direction (angle is 0°), the similarity is 1. When they are pointed in exact opposite directions (angle is 180°) it is -1, and for orthogonal vectors (angle is 90°) it is 0.

The result should be a matrix cosine_mat with dimensions ncol(q_mat) x ncol(r_mat) , in this example that would be 6x10:

cosine_mat <- qlcMatrix::cosSparse(q_mat, r_mat)

These cosines however have different levels of "support": For a given sample, only a fraction of rows contain non-zero values. When a pair of samples are compared, if a given row is 0 for both it will not contribute to the score. Example:

q_i <- c(0, 2, 5, -4, 0)
r_j <- c(0, 3, -5, 0, 2)
cos <- q_i %*% r_j / sqrt(sum(q_i^2)*sum(r_j^2))

q_sub <- c(2, 5, -4, 0)
r_sub <- c(3, -5, 0, 2)
cos_sub <- q_sub  %*% r_sub / sqrt(sum(q_sub^2)*sum(r_sub^2))

cos == cos_sub are the same, so here I consider the support to be 4 and scale by that level of support as a measure certainty for a given similarity. However, what I want is to only calculate the cosine similarity based on the variables where neither of them are 0.

q_sub2 <- c(2, 5)
r_sub2 <- c(3, -5)
cos_sub2 <- q_sub2  %*% r_sub2 / sqrt(sum(q_sub2^2)*sum(r_sub2^2))

cos_sub2 != cos. The difficulty is that the overlap for each q_i,r_j comparison is different.
Question 1: How do I go about that when my matrices are very large and apply() would probably be too slow?

Finally we it into a distance. That is, the higher the scaled similarity the lower the distance between the two samples.

# Boolean matrices which tells us where each matrix is non-zero
q_idx <- q_mat != 0
r_idx <- r_mat != 0

# Getting number of overlaps
n_overlaps <- t(q_idx) %*% r_idx

# Scale the cosines by log2 of the number of overlaps
scaling_factor <- log2(n_overlaps+1)
scaled_cosines <- cosine_mat * scaling_factor

# Turn the cosines into a distance measure
distances <- max(scaled_cosines) - scaled_cosines

These are the distance metrics I want to base my clustering on.
However, dist(distances) yields the following:

As far as I can tell, it finds the pairwise euclidean distances between each row of my distances matrix. I already have the distances I want to cluster on in distances, so what I want is to get the content of distances matrix as class "dist" so that I can use the hclust() function on them.
Question 2: How do I get my distances into a format that can be used by hclust?

[technocrat]

Thanks for continuing. Question

quote="kongcav, post:3, topic:162119"]
For a given sample, only a fraction of rows contain non-zero values
[/quote]

I'm not sure of this, because all rows have some non-zero values. Do you mean *all non-zero values?

(BTW: you can avoid having to take screenshots with a reprex. See the FAQ.)

library(Matrix)
q_mat <- new("dgeMatrix",
  Dim = 5:6, Dimnames = list(NULL, NULL), x = c(
    -2.5770364012495,
    0, 0, 2.54694632803317, 3.64904120269736, -3.02261588200774,
    0, 0, 0, 0, -2.04654404048837, -3.63879581531711, 0, 0, 0, 0,
    0, 0, -2.81866286398189, -3.66797842833383, 0, 0, 0, 0, 2.98110600049609,
    -2.19280397979525, 0, -2.8424060546161, -2.48547660452864, 0
  ),
  factors = list()
)

r_mat <- new("dgeMatrix",
  Dim = 5:6, Dimnames = list(NULL, NULL), x = c(
    -2.5770364012495,
    0, 0, 2.54694632803317, 3.64904120269736, -3.02261588200774,
    0, 0, 0, 0, -2.04654404048837, -3.63879581531711, 0, 0, 0, 0,
    0, 0, -2.81866286398189, -3.66797842833383, 0, 0, 0, 0, 2.98110600049609,
    -2.19280397979525, 0, -2.8424060546161, -2.48547660452864, 0
  ),
  factors = list()
)
r_mat <- new("dgeMatrix",
  Dim = c(5L, 10L), Dimnames = list(NULL, NULL),
  x = c(
    -3.4504049913605, 0, 0, 0, 0, 3.5394727773655, 0, 0,
    4.33940192113412, -5.86883647596701, 0, 2.33910643895182,
    0, -3.33773525083209, 2.26799438858444, 0, 0, 0, -3.27905564209673,
    0, 0, 0, 0, -3.42744251080144, 0, 0, 5.19680319250943, 0,
    0, 0, 0, 0, 0, 0, 3.15324351349785, 0, 0, 0, 0, 3.31553663832521,
    2.22957836928008, 0, 4.02176939483578, 0, 0, 0, 0, 2.21073872189316,
    0, 0
  ), factors = list()
)

cosine_mat <- qlcMatrix::cosSparse(q_mat, r_mat)
#> as(<dgeMatrix>, "dgCMatrix") is deprecated since Matrix 1.5-0; do as(., "CsparseMatrix") instead

rowSums(q_mat)
#> [1] -9.839000 -3.638796 -2.842406 -2.757193  2.962169
rowSums(r_mat)
#> [1]  2.318646  7.535910  6.232508 -5.704831  2.867938
rowSums(cosine_mat)
#> [1]  0.21030735  0.07880903 -1.27007299 -0.06901164  1.76275287  0.06055197