This is an interesting problem. I like the solution proposed by @etiennebr and I agree that the key part will be running sf::st_length() on a polygon to get the circumference.
I am afraid though that the solution proposed does not quite generalize: the sorting of points according to atan2 assumes that 1) the polygon is convex and 2) that the coordinate reference system has point zero somewhere inside the circle-like polygon. These assumptions may not be always met.
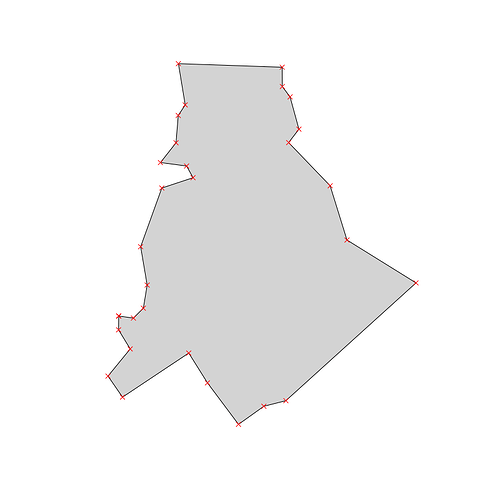
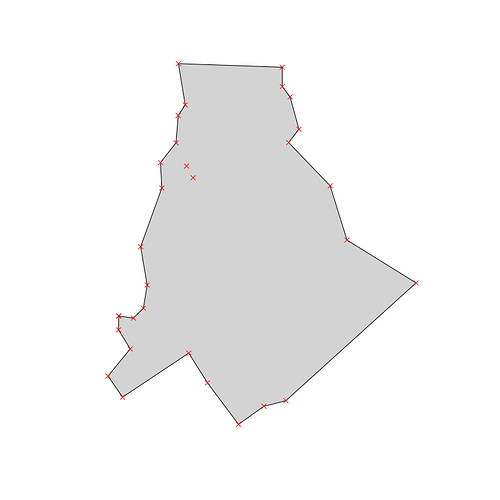
Consider this polygon - it is the county Mecklenburg from the well known & much liked North Carolina shapefile that ships with {sf}:
library(sf)
library(dplyr)
library(ggplot2)
shape <- st_read(system.file("shape/nc.shp", package="sf")) %>%
filter(CNTY_ID == 2041) %>% # Mecklenburg, as in Charlotte of Mecklenburg-Strelitz
st_transform(crs = 6543) # official planar CRS of NC
points <- st_cast(shape, "POINT") # raw points - how to interpret these??
plot(st_geometry(shape), col = "lightgrey")
plot(st_geometry(points), col = "red", pch = 4, add = T)
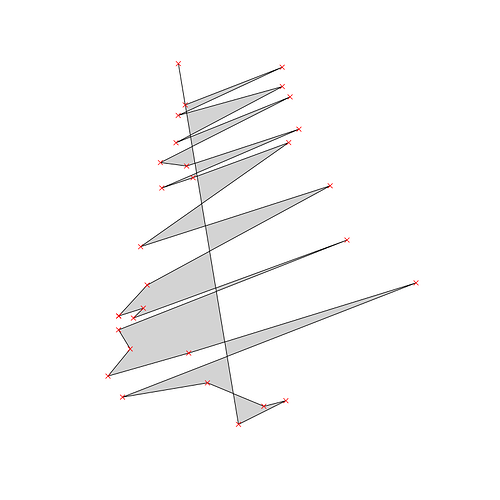
The shape is not convex, and the origin of the official North Carolina CRS is way outside of this polygon; as a consequence the ordering of points by atan2() values does not produce a satisfactory polygon:
points$atan2 <- atan2(st_coordinates(points)[, "X"],
st_coordinates(points)[, "Y"])
polygon <- points %>%
arrange(atan2) %>%
add_row(slice_head(.)) %>%
st_combine() %>%
st_cast("POLYGON")
plot(st_geometry(polygon), col = "lightgrey")
plot(st_geometry(points), col = "red", pch = 4, add = T)
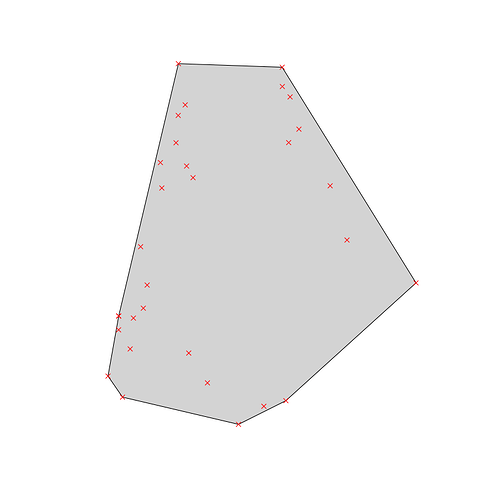
As an alternative I propose a different workflow: one that builds on sf::st_convex_hull() function.
The st_convex_hull() likes a multipoint object for its an argument, thus the st_union() call.
hull <- points %>%
st_union() %>%
st_convex_hull()
plot(st_geometry(hull), col = "lightgrey")
plot(st_geometry(points), col = "red", pch = 4, add = T)
A convex hull will approximate a circle nicely.
Should the convex hull give you too great a simplification you may consider a concave hull; an approach I like is via concaveman::concaveman(); it will take a points (ie. not a mutipoint) object as an argument + it has additional argument concavity to guide how closely it should hew to the data (polygons with concavity less than 1 can look rather silly).
hull <- points %>%
concaveman::concaveman(concavity = 5/4)
plot(st_geometry(hull), col = "lightgrey")
plot(st_geometry(points), col = "red", pch = 4, add = T)
Regardless of the approach to find your polygon the final call should be sf::st_length() on your polygon cast as a linestring to determine its circumference.
hull %>%
st_cast("LINESTRING") %>%
st_length()
539658.2 [US_survey_foot]