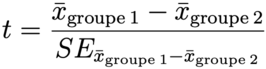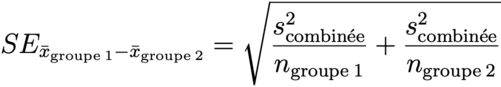Combined variance

[alx]

I am struggling recently since I need the means of two groups in order to perform a specific t test. I have been giving the following formulas where the second completes the denominator of the first.

What I don't understand is how to code these in R programming or the command for RStudio, also I wish to understand how or why the calculation is different from the standard error formula in order to find the combined variance.

[startz]

The formula is different because it allows for different variances in the two groups.

You might want to show what you've tried so far to get advice on coding.

[alx]

I tried the following:

t_result <- mean(med_vect) - mean(placebo_vect) / mean(med_vect)^2 - mean(med_vect)^2
t_result

This outputs [1] -85.58875 in the terminal.

I am unsure if this is the correct answer.

[startz]

Good start. A few things to change.

(1) You need parens around the difference in means. As written only the second mean is divided by the variance.
(2) You need a square root in the denominator.
(3) In computing the variances, you want var(med_vect), etc., rather than the square of the mean.
(4) You need to divide each variance by the number of observations.

[yifanliu]

@alx

t_result <- mean(med_vect) - mean(placebo_vect) / mean(med_vect)^2 - mean(med_vect)^2

I'm afraid the denominator part of this equation is absolutely not the one in the formula - isn't that ZERO?
at least it should be sth. like

sqrt(sd(c(med_vect, placebo_vect)) / length(med_vect) + sd(c(med_vect, placebo_vect)) / length(placebo_vect))

[technocrat]

d <- data.frame(
  mpg = c(
    22.8, 18.7, 14.3, 24.4, 22.8, 16.4, 17.3,
    15.2, 10.4, 10.4, 14.7, 32.4, 30.4, 33.9, 
    21.5, 15.5, 15.2, 13.3,19.2, 27.3, 26, 
    30.4, 15.8, 15, 21.4
  ),
  cyl = structure(c(
    1,2, 2, 1, 1, 2, 2, 2, 2, 2, 2, 1, 1, 1,
    1, 2, 2, 2, 2, 1, 1, 1, 2, 2, 1
  ), levels = c("4", "8"), class = "factor")
)

# classic t test
t.test(d$mpg ~ d$cyl, var.equal = TRUE)
#> 
#>  Two Sample t-test
#> 
#> data:  d$mpg by d$cyl
#> t = 8.1024, df = 23, p-value = 3.446e-08
#> alternative hypothesis: true difference in means between group 4 and group 8 is not equal to 0
#> 95 percent confidence interval:
#>   8.611261 14.516012
#> sample estimates:
#> mean in group 4 mean in group 8 
#>        26.66364        15.10000
# however equal variance assumption is violated
var.test(d$mpg~d$cyl)
#> 
#>  F test to compare two variances
#> 
#> data:  d$mpg by d$cyl
#> F = 3.1033, num df = 10, denom df = 13, p-value = 0.05925
#> alternative hypothesis: true ratio of variances is not equal to 1
#> 95 percent confidence interval:
#>   0.9549589 11.1197133
#> sample estimates:
#> ratio of variances 
#>           3.103299
# use Welsh test; confidence interval is for difference
# and does not include 0
t.test(d$mpg ~ d$cyl)
#> 
#>  Welch Two Sample t-test
#> 
#> data:  d$mpg by d$cyl
#> t = 7.5967, df = 14.967, p-value = 1.641e-06
#> alternative hypothesis: true difference in means between group 4 and group 8 is not equal to 0
#> 95 percent confidence interval:
#>   8.318518 14.808755
#> sample estimates:
#> mean in group 4 mean in group 8 
#>        26.66364        15.10000
# if asssumption that data are drawn from a normal distribution
# is doubtful, use the nonparametric test
wilcox.test(d$mpg ~ d$cyl)
#> Warning in wilcox.test.default(x = DATA[[1L]], y = DATA[[2L]], ...): cannot
#> compute exact p-value with ties
#> 
#>  Wilcoxon rank sum test with continuity correction
#> 
#> data:  d$mpg by d$cyl
#> W = 154, p-value = 2.775e-05
#> alternative hypothesis: true location shift is not equal to 0

^{Created on 2023-06-13 with reprex v2.0.2}

[yifanliu]

BTW, don't forget to use brackets. in your code

t_result <- mean(med_vect) - mean(placebo_vect) / mean(med_vect)^2 - mean(med_vect)^2

which equals

\overline{med\_vect} - \frac{\overline{placebo\_vect}}{(\overline{med\_vect})^2} - (\overline{med\_vect})^2

the very correct version of it should be:

(mean(med_vect) - mean(placebo_vect)) / sqrt(sd(c(med_vect, placebo_vect)) / length(med_vect) + sd(c(med_vect, placebo_vect)) / length(placebo_vect))