Coin flip simulation

General
1

I'm a beginner with R and I am trying to design a coin flip simulation. I want it to start by having a dollar amount of x. When I flip the coin and get heads I add one dollar. When I flip the coin and get tails, I lose a dollar. I want the simulation to end when I get a certain amount of money. Then, how do I run it several times to find the probability that I will end with that certain amount of money.

2

Hi! Welcome!

People here are interested in helping others learn R for themselves, so it will help if you can give the problem a try yourself and post whatever you come up with — even if it doesn’t work or is incomplete. Then we’ll be happy to help you figure out how to solve your problem from there! :grin:

Also, just in case this is related to something you’re doing for a class, you should take a look at our Homework Policy.

1 Like
3

Here is what I came up with:

x=1
out <- c(x+1, x-1)
flip <- sample(out, size=5, replace = TRUE)
flip

I can't seem to figure out how to add on to previously generated numbers and then stop the program when I reach certain numbers. And of course, figure out the probability as well

1 Like
4

Try this:

x <- 1
x + 1
#> [1] 2

# But x hasn't changed
x
#> [1] 1

# Reassign new value to the old variable name to keep it
x <- x + 1
x
#> [1] 2

Created on 2018-09-03 by the reprex package (v0.2.0).

Before worrying about this part, you might want to revisit your problem statement. Part of it doesn't quite add up, at least as far as I can tell:

If the simulation always flips coins until you've got your target amount of money, then the probability that a given run reaches that amount will be 1 because you designed it that way — it's going to keep flipping as long as it takes to get there, every time. So I suspect what you wrote down isn't quite what you want to do.

Setting aside for a moment exactly how it might be done, what's the overall goal of the simulation? Is it to determine the probability of winning a certain amount of money given a certain number of coin flips? Something else?

1 Like
5

Here's an approach using a matrix, for which you'll have to decide the maximum number of flips beforehand. It checks if each run ever goes above the amount within the maximum number of flips (not the probability of ending up with the amount). Packaged up in a function so we can rerun it easily,

flip_coins <- function(n_runs, n_flips, amount, prob = 0.5, seed = 47, plot = TRUE){
    set.seed(seed)    # so sampling is reproducible
  
    # make an n_runs x n_flips matrix of 0s and 1s
    flips <- matrix(rbinom(n_flips * n_runs, 1, prob), nrow = n_flips)
    # replace 0s with -1s so flips is now the amount won/lost for each flip
    flips[flips == 0] <- -1L
    # take a cumulative sum of each column to track total made/lost
    winnings <- apply(flips, 2, cumsum)
    
    if (plot){
        # plot cumulative winnings, with opacity
        matplot(winnings, type = 'l', col = "#00000022", lty = 1, xlab = "flip")
        abline(h = 0)    # break-even line
        abline(h = amount, col = "red")    # amount tested line
    }
      
    # check if winnings ever go above amount and divide by n_runs to get probability
    sum(colSums(winnings >= amount) > 0) / n_runs
}

flip_coins(n_flips = 100, n_runs = 10, amount = 5)


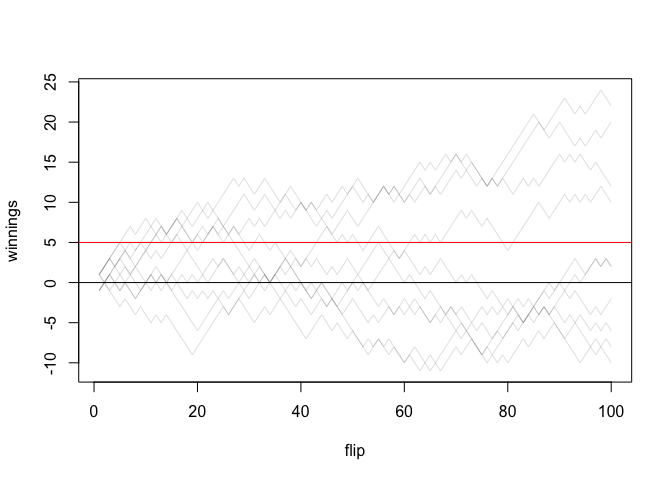
#> [1] 0.7

flip_coins(100, 100, 5)


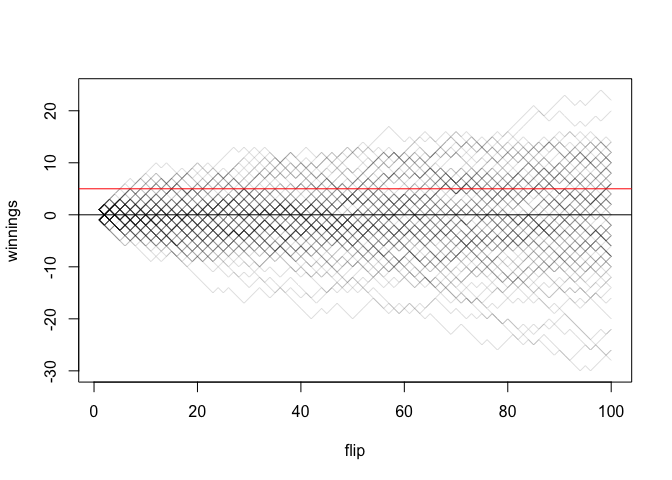
#> [1] 0.57

flip_coins(100, 1000, 25)


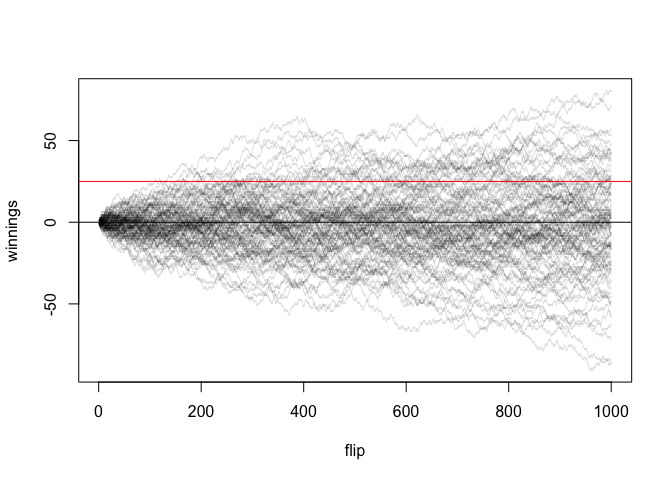
#> [1] 0.36

Messing with the probability of getting heads even a little (3%) can impact the result enormously:

flip_coins(100, 1000, 25, prob = 0.53)


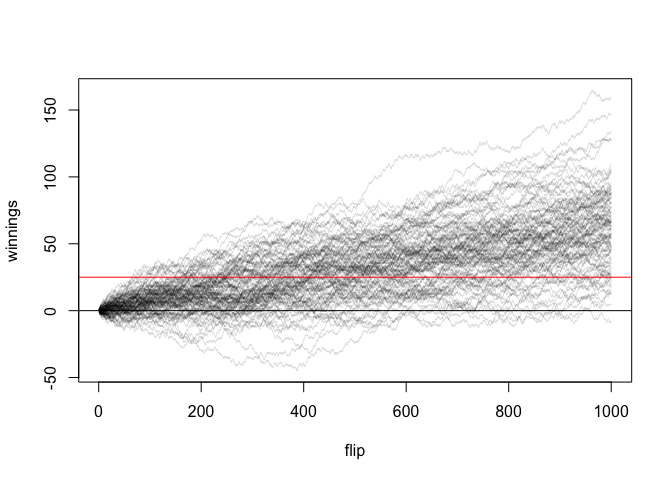
#> [1] 0.95
5 Likes