I am trying to simulate a queue with the following parameters:
lambda <- 5
mu <- 1
sim_time <- 200
k_minutes <- 15
num_simulations <- 100
initial_queue_size <- 100
time_step <- 1
lambda <- 5 # Arrival rate
mu <- 1 # Service rate
sim_time <- 200 # Simulation time
k_minutes <- 15 # Threshold for waiting time
num_simulations <- 100 # Number of simulations to run
initial_queue_size <- 100 # Initial queue size
time_step <- 1 # Time step for discretization
I simulated this code in R for 3 Servers vs 4 Servers:
library(dplyr)
library(ggplot2)
library(tidyr)
library(purrr)
library(gridExtra)
lambda <- 5
mu <- 1
sim_time <- 200
k_minutes <- 15
num_simulations <- 100
initial_queue_size <- 100
time_step <- 1
k_values <- c(3, 4)
run_simulation <- function(seed, k) {
set.seed(seed)
events <- data.frame(
time = c(0, cumsum(rexp(ceiling(sim_time * lambda), rate = lambda))),
type = "arrival"
)
events <- events[events$time <= sim_time, ]
queue <- numeric(initial_queue_size) # Initialize queue with initial_queue_size
servers <- numeric(k)
processed <- 0
waiting_times <- numeric()
results <- data.frame(
time = seq(0, sim_time, by = time_step),
queue_length = initial_queue_size,
processed_orders = 0,
waiting_longer = 0,
total_arrivals = initial_queue_size
)
event_index <- 1
for (i in 1:nrow(results)) {
current_time <- results$time[i]
# Process events up to current time
while (event_index <= nrow(events) && events$time[event_index] <= current_time) {
event_time <- events$time[event_index]
# Process completed services
finished <- servers <= event_time
if (any(finished)) {
processed <- processed + sum(finished)
servers[finished] <- 0
}
# Process new arrival
results$total_arrivals[i] <- results$total_arrivals[i] + 1
if (any(servers == 0)) {
free_server <- which(servers == 0)[1]
servers[free_server] <- event_time + rexp(1, mu)
waiting_times <- c(waiting_times, 0)
} else {
queue <- c(queue, event_time)
}
# Update queue
while (length(queue) > 0 && any(servers == 0)) {
free_server <- which(servers == 0)[1]
wait_time <- event_time - queue[1]
waiting_times <- c(waiting_times, wait_time)
servers[free_server] <- event_time + rexp(1, mu)
queue <- queue[-1]
}
event_index <- event_index + 1
}
results$queue_length[i] <- length(queue)
results$processed_orders[i] <- processed
results$waiting_longer[i] <- sum(waiting_times > k_minutes)
}
results
}
run_simulations <- function(k_values) {
map(k_values, function(k) {
map(1:num_simulations, ~run_simulation(., k)) %>%
set_names(paste0("sim_", 1:num_simulations))
}) %>% set_names(paste0("k", k_values))
}
simulations <- run_simulations(k_values)
process_results <- function(simulations) {
map_dfr(names(simulations), function(k_name) {
k <- as.integer(gsub("k", "", k_name))
bind_rows(simulations[[k_name]], .id = "simulation") %>%
mutate(k = k, simulation = as.integer(gsub("sim_", "", simulation))) %>%
group_by(simulation, k) %>%
mutate(
cumulative_waiting_longer = cumsum(waiting_longer),
cumulative_total_arrivals = cumsum(total_arrivals),
waiting_percentage = pmin(100, pmax(0, (cumulative_waiting_longer / cumulative_total_arrivals) * 100))
) %>%
ungroup()
})
}
all_results <- process_results(simulations)
plot_waiting_percentage <- function(data, k) {
ggplot(data %>% filter(k == !!k), aes(x = time, y = waiting_percentage, group = simulation)) +
geom_line(alpha = 0.1, color = "blue") +
stat_summary(fun = mean, geom = "line", aes(group = 1), color = "red", size = 1) +
labs(title = paste("Percentage of People Waiting >", k_minutes, "Minutes (k=", k, ")"),
subtitle = paste("Arrival Rate =", lambda, ", Service Rate =", mu),
x = "Time", y = "Percentage") +
theme_minimal() +
ylim(0, 100)
}
plot_queue_length <- function(data, k) {
ggplot(data %>% filter(k == !!k), aes(x = time, y = queue_length, group = simulation)) +
geom_line(alpha = 0.1, color = "blue") +
stat_summary(fun = mean, geom = "line", aes(group = 1), color = "red", size = 1) +
labs(title = paste("Queue Length Over Time (k=", k, ")"),
subtitle = paste("Arrival Rate =", lambda, ", Service Rate =", mu, ", Initial Queue Size =", initial_queue_size),
x = "Time", y = "Queue Length") +
theme_minimal() +
scale_y_continuous(expand = c(0, 0), limits = c(0, NA)) # Start y-axis from 0
}
plot_cumulative_orders <- function(data, k) {
ggplot(data %>% filter(k == !!k), aes(x = time, y = processed_orders, group = simulation)) +
geom_line(alpha = 0.1, color = "blue") +
stat_summary(fun = mean, geom = "line", aes(group = 1), color = "red", size = 1) +
labs(title = paste("Cumulative Orders Processed (k=", k, ")"),
subtitle = paste("Arrival Rate =", lambda, ", Service Rate =", mu, ", Initial Queue Size =", initial_queue_size),
x = "Time", y = "Cumulative Orders") +
theme_minimal() +
scale_y_continuous(expand = c(0, 0), limits = c(0, NA))
}
plots <- map(k_values, function(k) {
list(
waiting_percentage = plot_waiting_percentage(all_results, k),
queue_length = plot_queue_length(all_results, k),
cumulative_orders = plot_cumulative_orders(all_results, k)
)
})
do.call(grid.arrange, c(unlist(plots, recursive = FALSE), ncol = 2))
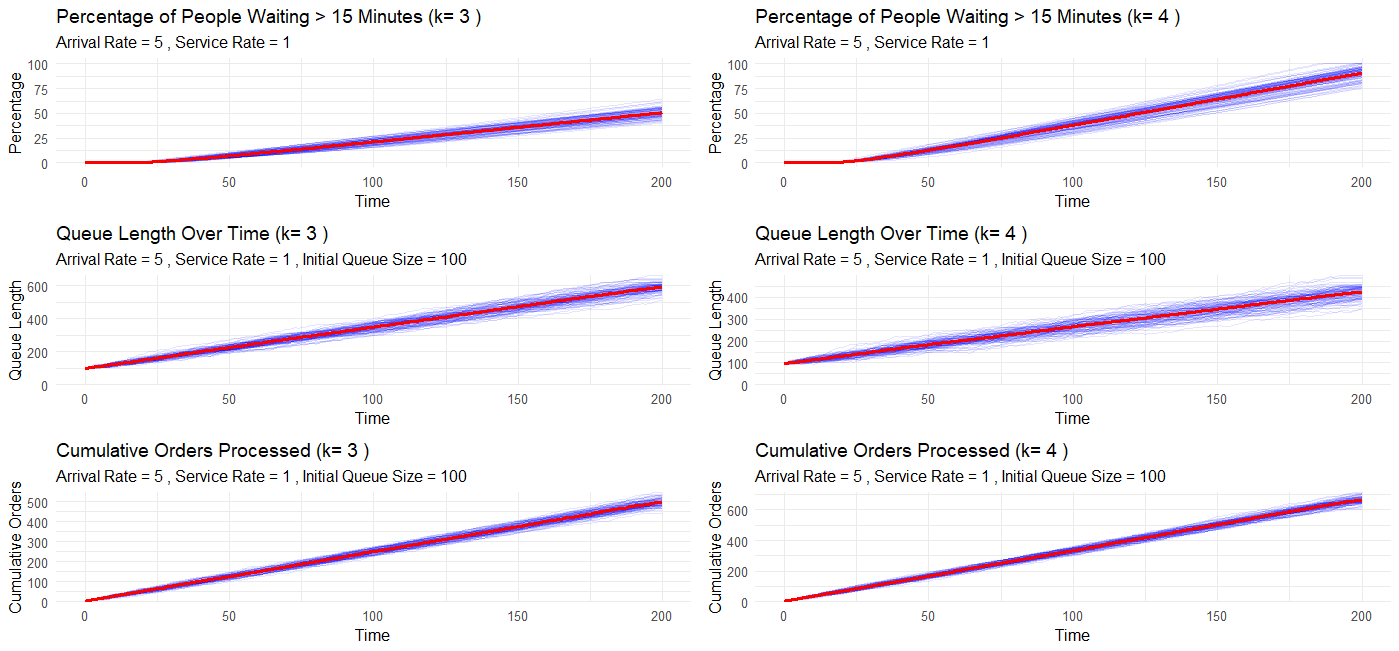
Based on these results, we can see that on average, the same queue with 4 servers outperforms the 3 server queue for cumulative orders processed and queue length - but somehow the percent of customers waiting longer than 15 minutes is better (i.e. increases slower) for 3 servers than 4 servers? I think this might be a problem with the way my function is calculating percentages
Can someone please help me review and find where the mistake is?