This is a companion discussion topic for the original entry at https://rviews.rstudio.com/2020/11/02/simulating-biologically-plausible-survival-data
In two recent posts, one on the Disease Progression Model and the other on Fake Data, I highlighted some of R's tools for simulating data that exhibit desired correlations and other statistical properties. In this post, I’ll focus on a small cluster of R packages that support generating biologically plausible survival data.
Background
In an impressive paper Simulating biologically plausible complex survival data Crowther & Lambert (2013) that combines survival analysis theory and numerical methods, Michael Crowther and Paul Lambert address the problem of simulating plausible data in which event time, censuring and covariate distributions are plausible. They develop a methodology for conducting survival analysis studies, and also provide computational tools for moving beyond the usual exponential, Weibull and Gompertz models. Building on the work by Bender et al. (2005) in establishing a framework for simulating survival data for Cox proportional hazards models, Crowther and Lambert discuss how modelers can incorporate non proportional model hazards, time varying effects, delayed entry and random effects and provide code examples based on the Stata survsim package.
The survsim package
Not longer after the Stata package appeared, Moriña and Navarro released the R survsim package which implements some of the features in the Stata package for simulating complex survival data. The R package does not have a vignette, but you can find several examples in the JSS paper Moriña & Navarro (2014).
The following example from section 4.3 of the paper simulates adverse events for a clinical trial with 100 patients followed up for 30 days. The authors suggest that the three covariates x could represent body mass index, age at entry to the cohort, and whether or not the subject has hypertension. This is a little bit unusual and sophisticated example of survival modeling.
set.seed(12345)
dist.ev <- c("weibull", "llogistic", "weibull")
anc.ev <- c(0.8, 0.9, 0.82)
beta0.ev <- c(3.56, 5.94, 5.78)
beta <- list(c(-0.04, -0.02, -0.01), c(-0.001, -0.0008, -0.0005),c(-0.7, -0.2, -0.1))
x <- list(c("normal", 26, 4.5), c("unif", 50, 75), c("bern", 0.25))
clinical.data <- mult.ev.sim(n = 100, # number of patients in cohort
foltime = 30, # maximal followup time
dist.ev, # time to event distributions (t.e.d.)
anc.ev, # parameters for t.d.e. distributions
beta0.ev, # beta0 parameters for t.d.e. dist
dist.cens = "weibull", #censoring distribution
anc.cens = 1, # parameters for censoring dist
beta0.cens = 5.2, # beta0 for censoring dist
z = list(c("unif", 0.6, 1.4)), # random effect dist
beta, # effect of covariate
x, # distributions of covariates
nsit = 3) # max number of adverse events for an individual
head(round(clinical.data,2))
## nid ev.num time status start stop z x x.1 x.2
## 1 1 1 5.79 1 0 5.79 0.97 28.63 69.02 1
## 2 1 2 30.00 0 0 30.00 0.97 28.63 69.02 1
## 3 1 3 30.00 0 0 30.00 0.97 28.63 69.02 1
## 4 2 1 3.37 1 0 3.37 0.60 36.42 53.81 0
## 5 2 2 30.00 0 0 30.00 0.60 36.42 53.81 0
## 6 2 3 30.00 0 0 30.00 0.60 36.42 53.81 0
The simsurv package
In the vignette on *How to use the simsurv package, the package authors Sam Brilleman and Alessandro Gasparini state that they directly modeled their package on the Stata package survsim and cite the Crowther and Lambert paper. They show how survsim builds out much of the functionality envisioned there in examples that demonstrate the interplay between model fitting and simulation. Example 2 of the vignette is concerned with constructing fake data modeled on the German breast cancer data by Schumacher et al. (1994).
data("brcancer")
head(brcancer)
## id hormon rectime censrec
## 1 1 0 1814 1
## 2 2 1 2018 1
## 3 3 1 712 1
## 4 4 1 1807 1
## 5 5 0 772 1
## 6 6 0 448 1
The example begins by fitting alternative models to the data using functions from the flexsurv package of Jackson, Metcalfe and Amdahl. Two candidate models are proposed and a spline model giving the best fit is used to simulate data. The example concludes with more model fitting to examine the fake data. All of the examples in the vignette showcase the interplay between simsurv and flexsurv functions and emphasize the flexible modeling tools in flexsruv for building custom survival models.
The following code replicates the portion of Example 2 that illustrates the use of the flexsurvspline() function which allows the calculation of the log cumulative hazard function to depend on knot locations.
The code below produces the simulated data and uses the survminer package of Kassambara et al. to produce high quality Kaplan-Meier plots.
This line of code fits a three knot spline model to the brcancer data. The flexsurvspline() function, as with other functions in the flexsurv package build on the basic functionality of the fundamental Terry Therneau’s survival package.
true_mod <- flexsurv::flexsurvspline(Surv(rectime, censrec) ~ hormon,
data = brcancer, k = 3)
This helper function returns the log cumulative hazard at time t
logcumhaz <- function(t, x, betas, knots) {
# Obtain the basis terms for the spline-based log
# cumulative hazard (evaluated at time t)
basis <- flexsurv::basis(knots, log(t))
# Evaluate the log cumulative hazard under the
# Royston and Parmar specification
res <-
betas[["gamma0"]] * basis[[1]] +
betas[["gamma1"]] * basis[[2]] +
betas[["gamma2"]] * basis[[3]] +
betas[["gamma3"]] * basis[[4]] +
betas[["gamma4"]] * basis[[5]] +
betas[["hormon"]] * x[["hormon"]]
res
}
The simsurv() functions generates the simulated survival data.
covariates <- data.frame(id = 1:686, hormon = rbinom(686, 1, 0.5))
sim_data <- simsurv(
betas = true_mod$coefficients, # "true" parameter values
x = covariates, # covariate data for 686 individuals
knots = true_mod$knots, # knot locations for splines
logcumhazard = logcumhaz, # definition of log cum hazard
maxt = NULL, # no right-censoring
interval = c(1E-8,100000)) # interval for root finding
sim_data <- merge(covariates, sim_data)
head(sim_data)
## id hormon eventtime status
## 1 1 1 240.4 1
## 2 2 0 942.6 1
## 3 3 1 463.5 1
## 4 4 0 1762.0 1
## 5 5 0 3976.0 1
## 6 6 0 2288.0 1
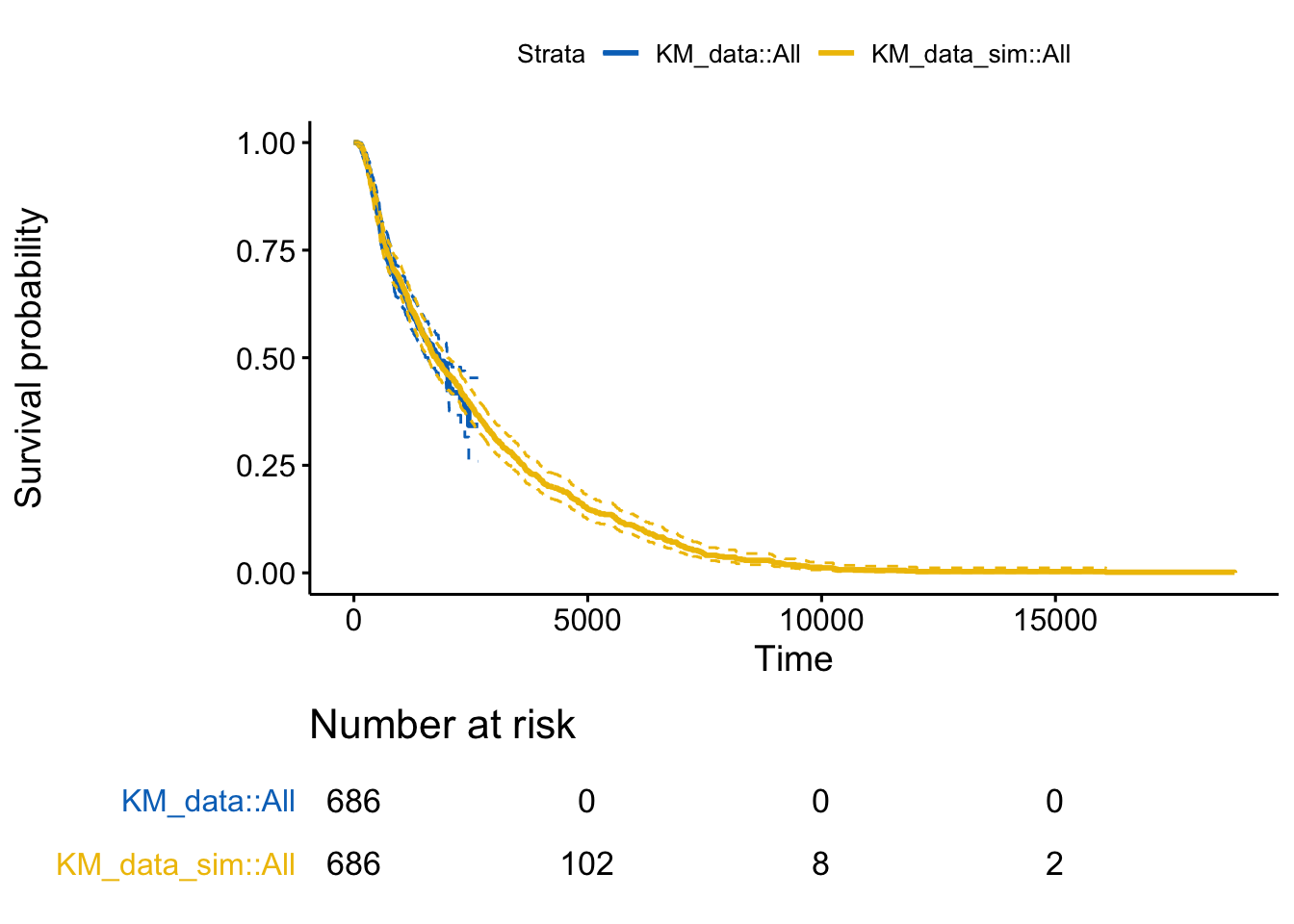
We use the surv_fit function from the survminer package to fit the Kaplan-Meier curves
KM_data <- survminer::surv_fit(Surv(rectime, censrec) ~ 1, data = brcancer)
KM_data_sim <- survminer::surv_fit(Surv(eventtime, status) ~ 1, data = sim_data)
Finally, plotting the curves shows that the simulsted data does appear to plausibly resemble the original data.
p <- ggsurvplot_combine(list(KM_data, KM_data_sim),
risk.table = TRUE,
conf.int = TRUE,
censor = FALSE,
conf.int.style = "step",
tables.theme = theme_cleantable(),
palette = "jco")
plot.new()
print(p,newpage = FALSE)
I hope you find this small post helpful. The CRAN task view on Survival Analysis is a fantastic resource, but it can be a daunting task for non-experts to know where to begin to unravel the secrets there without a thread to pull on.