Bimodality in log distribution

[jayant]

Hello Colleagues,
Good afternoon!

I am trying to understand from scratch the working of log() transformation in ggplot(). I have used the following code to observe the distribution of the variable actor_1_facebook_likes on the attached dataset.
https://www.dropbox.com/s/eognre5qbsr1osk/dat_test.csv?dl=0

ggplot(movie_select %>% filter(!is.na(actor_1_facebook_likes)),aes(log10(actor_1_facebook_likes)))+
  #scale_x_log10()+
  geom_histogram(fill="tomato",binwidth=.25)+
  labs(y="Count of Leading Actors",title="Facebook Popularity for Leading Actor")

Please find the plot attached.

Here are my two questions about the plot:

• First, why is the log distribution bimodal, whereas the original histogram was right-skewed.

• Next, we see that on the x-axis the value of 3 which is same as log(1000) to the base 10 is showing up a bit more than 1000 times, count on the y-axis. But in the actual data, the value of 1000 for actor_1_facebook_likes is not showing up 1000 times. May I know what is happening here?

Explanation/help is greatly appreciated.

[joels]

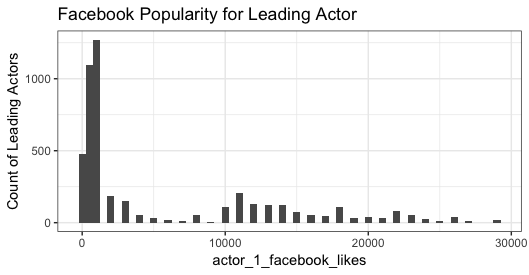
The data are actually multimodal (and right skewed) and the log transformation doesn't change the multimodal-ness. For example, in this untransformed histogram, in addition to the peak centered at 1,000 likes, note the peak at 11,000 likes, plus smaller peaks at higher values of likes. The log transformation just reduces the skew of the distribution:

library(tidyverse) 
theme_set(theme_bw())

ggplot(movie_select %>% filter(actor_1_facebook_likes < 30000), aes(actor_1_facebook_likes)) +
  geom_histogram(binwidth=500) +
  labs(y="Count of Leading Actors",title="Facebook Popularity for Leading Actor")

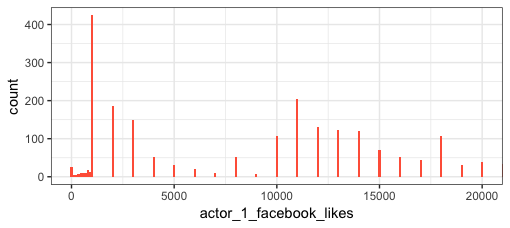
Or, rather than binning the data, look at direct counts of each discrete value of actor_1_facebook_likes:

ggplot(movie_select, aes(actor_1_facebook_likes)) +
  geom_bar(width=100, fill="tomato") +  # Large width, otherwise bars are to thin to be visible
  coord_cartesian(xlim=c(0,2e4))

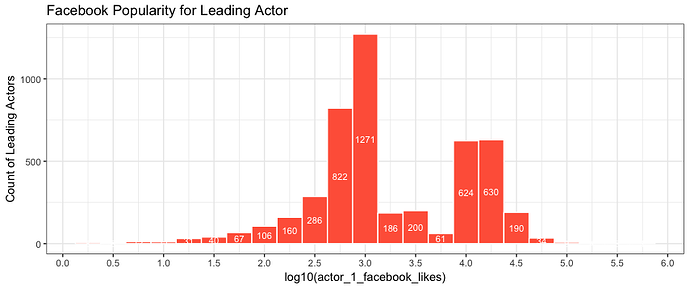
As for the number of counts for the bin centered at log10=3: The binwidth is denominated on the log scale with binwidth=0.25. That particular bin ranges from 2.875 to 3.125. Now transform that back to unlogged values to see the range of the bin on the scale of the data:

bin = 10^c(2.875, 3.125)
bin
[1]  749.8942 1333.5214

Now count the number of data values within that range:

sum(between(movie_select$actor_1_facebook_likes, bin[1], bin[2]), na.rm=TRUE)
[1] 1,271

Compare this with your plot, but with bin counts added:

ggplot(movie_select, aes(log10(actor_1_facebook_likes)))+
  geom_histogram(fill="tomato",binwidth=.25, colour="white") +
  stat_bin(binwidth=.25, geom="text", aes(label=..count.., y=0.5*..count..), colour="white", size=3) +
  labs(y="Count of Leading Actors",title="Facebook Popularity for Leading Actor") +
  scale_x_continuous(breaks=seq(0, 6, 0.5))

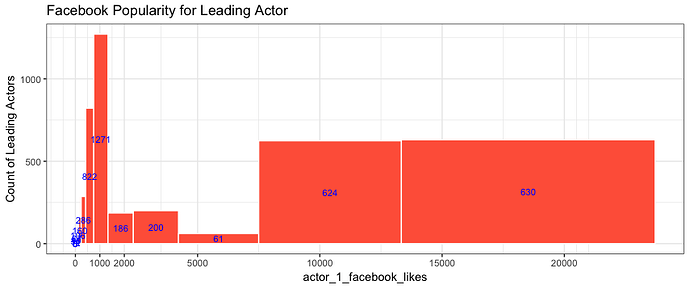
Here's what the logged bins look like on the scale of the data:

bins = 10^(seq(-1,4.3,0.25) + 0.125)

ggplot(movie_select %>% filter(actor_1_facebook_likes < 30000),
       aes(actor_1_facebook_likes)) +
  geom_histogram(fill="tomato", breaks=bins, colour="white") +
  stat_bin(breaks=bins, geom="text", 
           aes(label=..count.., y=0.5*..count..), colour="blue", size=3) +
  labs(y="Count of Leading Actors",title="Facebook Popularity for Leading Actor") +
  scale_x_continuous(breaks=c(0,1000,2000,seq(5000,25000,5000)))

[jayant]

Thanks for your explanation. I was reading the histogram incorrectly.