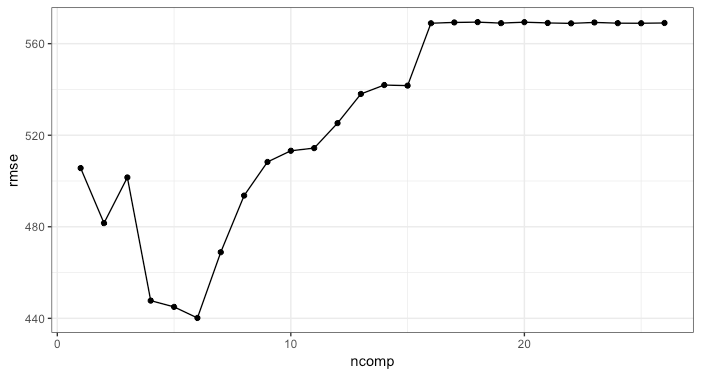
Here's a tidy workflow that I used to see if estimating the transformations inside of resampling made a big difference (it didn't):
library(recipes)
library(rsample)
library(yardstick)
# create the recipe without the formula to more easily
pls_rec <- recipe(total_N2O ~ ., data = annual_flux) %>%
add_role(series, town, avg_N2O, log_avg_N2O,year, log_total_N2O,
new_role = "other data") %>%
step_YeoJohnson(all_predictors()) %>%
step_center(all_predictors()) %>%
step_scale(all_predictors())
# functions to fit the model and get predictions + RMSE
pls_fit <- function(recipe, ...) {
plsr(total_N2O ~ ., data = juice(recipe, all_predictors(), all_outcomes()))
}
pls_pred <- function(split, recipe, model, ...) {
# get the holdout data via `assessment` then preprocess
pred_data <- bake(recipe, newdata = assessment(split), all_predictors(), all_outcomes())
# One outcome so drop the dimension to a 2d array
pred_vals <- predict(model, newdata = pred_data)[,1,] %>%
as.data.frame() %>%
bind_cols(assessment(split) %>% select(total_N2O)) %>%
# drop the predictions per component into a long df
gather(label, prediction, -total_N2O) %>%
# convert "X comp" to a numeric X
mutate(
ncomp = gsub(" comps", "", label),
ncomp = as.numeric(ncomp)
) %>%
# add resampling labels
cbind(labels(split))
}
# setup a resampling scheme, estimate the recipes, fit the models and
# make predictions,
set.seed(57256)
folds <- vfold_cv(annual_flux, repeats = 5) %>%
mutate(
recipes = map(splits, prepper, pls_rec, retain = TRUE),
models = map(recipes, pls_fit, validation = "none"),
pred = pmap(
list(split = splits, recipe = recipes, model = models),
pls_pred
)
)
# get the RMSE values, summarize by #comps and plot
pred_vals <- folds %>%
pull(pred) %>%
bind_rows()
performance <- pred_vals %>%
group_by(ncomp, id, id2) %>%
do(metrics(., truth = total_N2O, estimate = prediction))
av_performance <- performance %>%
group_by(ncomp) %>%
summarize(rmse = mean(rmse), rsq = mean(rsq))
ggplot(av_performance, aes(x = ncomp, y = rmse)) +
geom_point() +
geom_line() +
theme_bw()
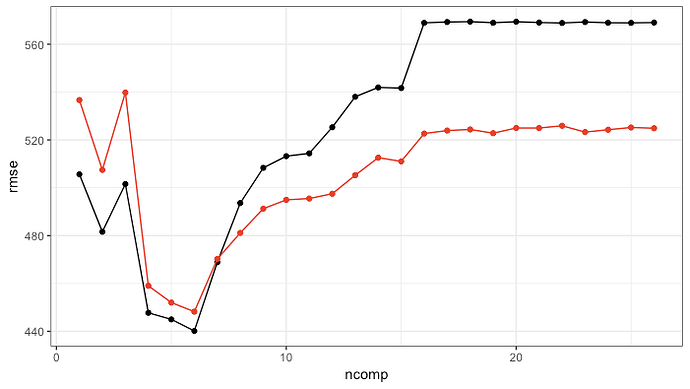
We can compare this to what comes out of plsr (very similar pattern) via
# compare to orignal objects
original_pls_model <-
data.frame(
ncomp = 0:26,
rmse = unname(RMSEP(plsFit)$val[1,1,]),
rsq = unname(R2(plsFit)$val[1,1,])
) %>%
filter(ncomp > 0)
# pretty consistent with the original model; values are different due
# to different resamples (and more too)
ggplot(av_performance, aes(x = ncomp, y = rmse)) +
geom_point() +
geom_line() +
geom_point(data = original_pls_model, col = "red") +
geom_line(data = original_pls_model, col = "red") +
theme_bw()