AUC function in DescTools (version 0.99.28)

[LauraL]

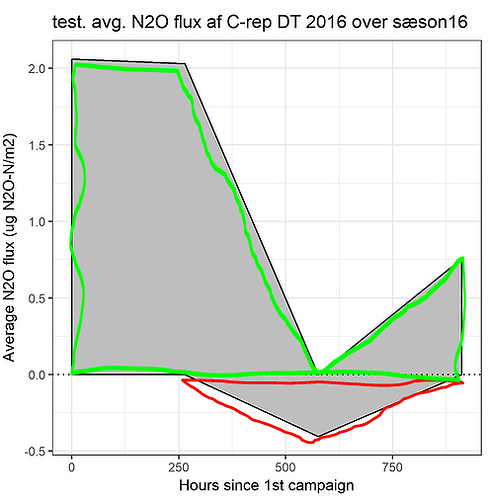
Hi there.
I'm working in RStudio, and were very happy to find the AUC function in DescTools (version 0.99.28).
The only thing is, that i want to be absolutely sure how the function works, when i have some negative Y-axis values.
The negative area beneath the x-axis (red area) must be subtracted from the positive area (green).
I've tried to use all 3 methods ( "trapezoid", "step" and "spline"), when calculating AUC, they all work just fine, I just dont know which one gives me the correct answer.
So my question is: which of the 3 methods do i need to use? It is not clear to me, when reading the description in help.
Many thanks - Laura!

[Yarnabrina]

If I understand correctly, what you want is to subtract the area under the x-axis and above the curve [green in the plot] from the area above the x-axis and the curve [red in the plot]. Is that right?

If so, then though I don't know the correct answer, but I can provide you a counter example where step and spline gives wrong results. Please keep in mind that this doesn't prove that trapezoid is correct always.

# dummy points
u <- c(1, 3, 5, 4)
v <- c(2, 0, -2, 0)

# plot
plot(x = u,
     y = v)
polygon(x = c(1, 1, 3),
        y = c(0, 2, 0),
        col = "green",
        border = "green")
polygon(x = c(3, 5, 4),
        y = c(0, -2, 0),
        col = "red",
        border = "red")
abline(h = 0)

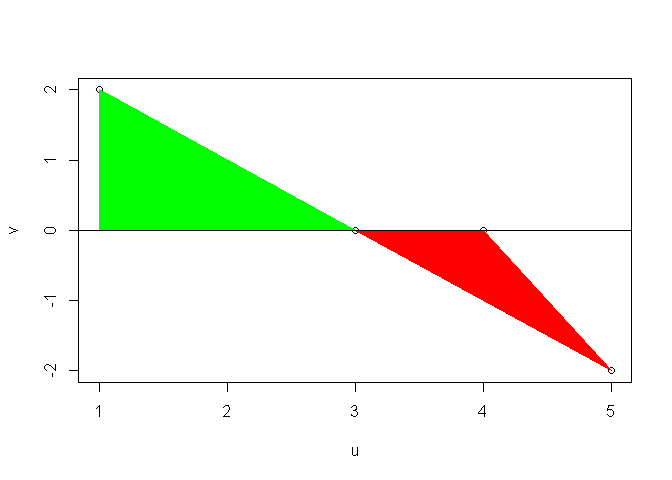
# expected answer
(0.5 * 2 * 2) - (0.5 * 1 * 2)
#> [1] 1

# DescTools results
sapply(X = c("trapezoid", "step", "spline"),
       FUN = DescTools::AUC,
       x = u,
       y = v)

#> trapezoid      step    spline 
#> 1.0000000 4.0000000 0.6956522

^{Created on 2019-04-18 by the reprex package (v0.2.1)}

For your reference, here's the source code:

AUC <- function(x, y, method=c("trapezoid", "step", "spline"), na.rm = FALSE) {

  # calculates Area unter the curve
  # example:
  #   AUC( x=c(1,2,3,5), y=c(0,1,1,2))
  #   AUC( x=c(2,3,4,5), y=c(0,1,1,2))

  if(na.rm) {
    idx <- na.omit(cbind(x,y))
    x <- x[idx]
    y <- y[idx]
  }

  if (length(x) != length(y))
    stop("length x must equal length y")

  idx <- order(x)
  x <- x[idx]
  y <- y[idx]

  switch( match.arg( arg=method, choices=c("trapezoid","step","spline") )
          , "trapezoid" = { a <- sum((apply( cbind(y[-length(y)], y[-1]), 1, mean))*(x[-1] - x[-length(x)])) }
          , "step" = { a <- sum( y[-length(y)] * (x[-1] - x[-length(x)])) }
          , "spline" = { a <- integrate(splinefun(x, y, method="natural"), lower=min(x), upper=max(x))$value }
  )
  return(a)
}

[LauraL]

Hi Yarnabrina, thanks for answering, i just tried to visualize my intention better,.
I want to calculate a total area (the green+red marking on my graph) and subtract the red area (being the area under the x axis) from the total. Does it make sense?

As you, i get different results from the three different methods, but i also believe the Trapezoid is the most realistic for my data, but i have to be sure (before using the results for up-scaling of my gas emissions)

[Yarnabrina]

@LauraL

As you, i get different results from the three different methods

My point was not the different results. I wanted to point out that the result from trapezoid matches the answer I expected, where those from other two did not.

@LauraL

i have to be sure

I provided you the source code above, so you may have a better insight from that. The best way will be to modify the source code for your own purpose.

@LauraL

I want to calculate a total area (the green+red marking on my graph) and subtract the red area (being the area under the x axis) from the total. Does it make sense?

What I understand from this is that you want the area of the (green + red) - red = green part. So, you'll be ignoring the parts under the x-axis completely.

If you've functional from of the curve, say f, just define g = max(f, 0) and integrate it out. It should give the correct result.

If you've the coordinates only, then one option will be to find the points where the curve will cross the x-axis and then consider only those points along with points above x-axis and find AUC based on these (using trapezoid). That works (see below), but in case there are many crossings, doing it manually will be difficult.

# dummy points
u <- c(1, 2, 3, 4)
v <- c(2, -3, 1, -4)

# plot
plot(x = u,
     y = v)
abline(h = 0)
polygon(x = c(1, u, 4),
        y = c(0, v, 0),
        col = "green")
segments(x0 = c(1, 4),
         y0 = c(2, -4),
         y1 = c(0, 0))
clip(x1 = min(u),
     x2 = max(u),
     y1 = min(v),
     y2 = 0)
polygon(x = c(1, u, 4),
        y = c(0, v, 0),
        col = "red")

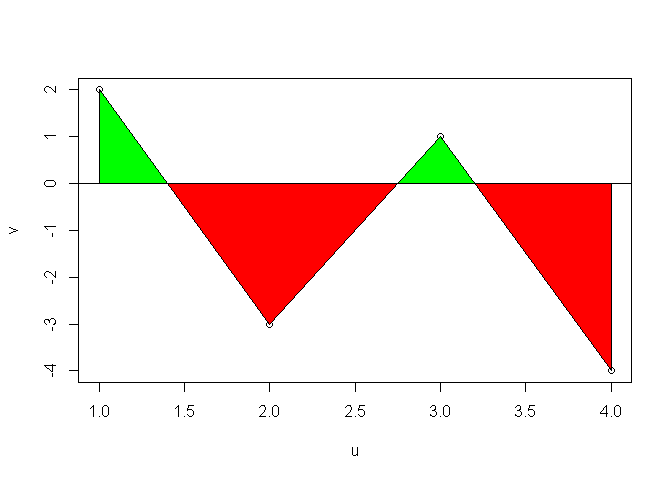
# expected answer
(0.5 * (1.4 - 1) * 2) + (0.5 * (3.2 - 2.75) * 1)
#> [1] 0.625

# DescTools results
sapply(X = c("trapezoid", "step", "spline"),
       FUN = DescTools::AUC,
       x = c(1, 1.4, 2.75, 3, 3.2),
       y = c(2, 0, 0, 1, 0))
#>  trapezoid       step     spline 
#>  0.6250000  1.0000000 -0.8724935

^{Created on 2019-04-19 by the reprex package (v0.2.1)}

I don't know a good solution, may be someone else will provide one. If you find one yourself, please share that solution here as that'll be helpful for anyone else having same problem in future.

Good luck!

[LauraL]

Hi again, sorry for the confusion, I just realized i've my post last night (way to late for me to think clear apparently) where i tried to be more precise, is wrong.
I've edited the original post.
As you (nearly) started out saying, I wish to calculate a total area (green) above the x axis, and then a total area beneath the x axis (red), and then subtract the total (negative) red area from the total (positive) green area.
I have several 100 different graphs to calculate an AUC on, and hence I want to avoid a manual solution for finding cross points, due to some of them have several crossings (in one graph) as you also write.
I dont have a function for the graphs, they are all unique.
The second graph you provided is also how many of mine looks like.
I combined the two of your answers, and calculated manually to check the result, and found the trapezoid to be correct. Many thanks - it was of great help!
I want to paste the code correctly (same way as you, so its not just a comment), but dont know how.

Here is the combined code from you, that gives me the correct answer.

u <- c(1, 2, 3, 4)
v <- c(2, -3, 1, -4)

plot(x = u,
     y = v)
abline(h = 0)
polygon(x = c(1, u, 4),
        y = c(0, v, 0),
        col = "green")
segments(x0 = c(1, 4),
         y0 = c(2, -4),
         y1 = c(0, 0))
clip(x1 = min(u),
     x2 = max(u),
     y1 = min(v),
     y2 = 0)
polygon(x = c(1, u, 4),
        y = c(0, v, 0),
        col = "red")

sapply(X = c("trapezoid", "step", "spline"),
       FUN = DescTools::AUC,
       x = u,
       y = v)
# trapezoid   step   spline
# -3           0      -3

#expected answer
(0.5 * (1.4 - 1) * 2) +
  (0.5 * (2.75-1.4) * -3) +
  (0.5 * (3.2 - 2.75) * 1) +
  (0.5 * (4-3.2) * -4)

#[1] -3

[Yarnabrina]

@LauraL

I wish to calculate a total area (green) above the x axis, and then a total area beneath the x axis (red), and then subtract the total (negative) red area from the total (positive) green area.

This makes much more sense. I was very surprised in your earlier post, to be honest.

Since you've figured out that trapezium is the best, for each of the graphs (that you have to do), you'll just have to do DescTools::AUC(x = u, y = v), where u and v respectively store the abscissa and ordinate. It works since trapezoid is the default method.

Obviously, you don't need to plot all the graphs (you can, if you want), and since you'll use only one method, sapply is not necessary anymore.

@LauraL

I want to paste the code correctly (same way as you, so its not just a comment), but dont know how.

That's actually simple. All you've to do is to place your code in between a pair of triple backticks (```). Or, paste the code, select it, and click the </> button in the toolbar above. You may try to edit your earlier post.

Now that your problem is solved, will you consider marking this thread as solved? Feel free to choose one of your own posts.

If you don't know how, take a look at this post:

FAQ: How do I mark a solution?

If your question has been answered, don't forget to mark the solution! How do I mark a solution? Find the reply you want to mark as the solution and look for the row of small gray icons at the bottom of that reply. Click the one that looks like a box with a checkmark in it: [image] Hovering over the mark solution button shows the label, "Select if this reply solves the problem". If you don't see the mark solution button, try clicking the three dots button ( ••• ) to expand the full set of options. When a solution is chosen, the icon turns green and the hover label changes to: "Unselect if this reply no longer solves the problem". Success! [solution_reply_author] …

[LauraL]

I've marked all three solutions as answers, since it is the combination that made me realize trapezoid is the correct method for AUC in my case. Many thanks again!