More of a general statistics question rather than about R specifically, but I didn't know where to post this, so if anyone can help, it would be hugely appreciated!
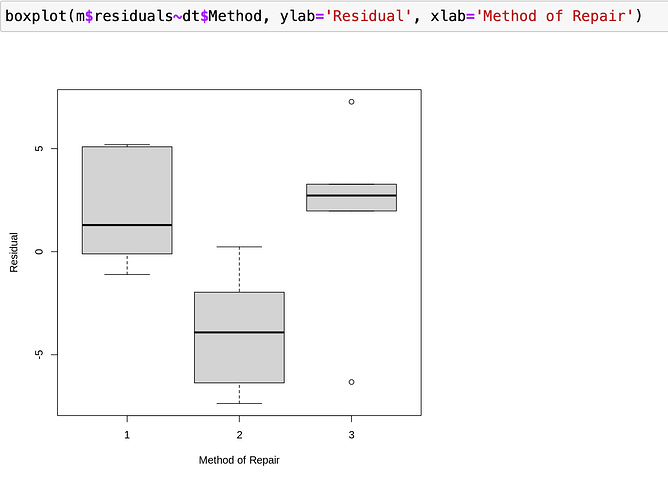
I am trying to assess the conditions for ANOVA, specifically the condition in question that residuals must be normally distributed. I first did a boxplot to visually assess the data and from the boxplot, the residuals do not look normal, or at least each group's residuals are not centered on zero:
After seeing the boxplots, I did a normal quantile plot to investigate further, and from the normal quantile plot the data does appear to be normal. I would post a screenshot but I'm limited to one photo per post, this was my code:
qqnorm(m$residuals, pch=16)
qqline(m$residuals, col="red", lwd=3)
From what I understand, it appears that my residuals are normally distributed, but do not have a mean of zero. What I am wondering is if zero mean is a condition for ANOVA? I know that residuals have to be normally distributed but do they also have to have zero mean?