arm::bayesglm how to interpret results?

[HNSKD]

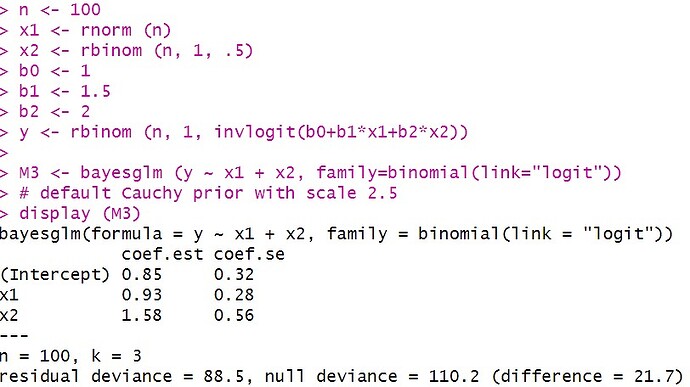
Help guys. I am using arm::bayesglm function to run the Bayesian logistic regression in R. But I am clueless of how to interpret the output.

[sturu]

I don't know this package specifically but I do quite a bit of Bayesian regression modelling using brms/stan.

I suspect you'll have to answer quite a few questions for us to understand your needs & be able to help:

What metrics would you normally look for when interpreting output of regression models?

Would you be more comfortable interpreting the output if the coefficients were converted to odds ratios?

How did you choose the variables to include in the model you've created?

Is this model the best? (& how did you decide?)

[HNSKD]

Thanks for the reply @sturu
Typically, when I do the classical frequentist approach of logistic regression, I would present the OR with the 95% confidence interval. As for the bayesian logistic regression, I am confused about what the coef.est and coef.se mean? I read a paper where the author compares the 2 approaches:

• In the classical approach, he wrote "The odds of natural dental caries have decreased by 27.4% for patients with age group 25–35 compared to the reference group."

• In the bayesian approach, he wrote "we found out that males are 81.6% most less likely to have natural dental caries compared to females."

Ref: Bayesian model with application to a study of dental caries | BMC Oral Health | Full Text

In the classical approach, he uses the term "odds", but in the bayesian, he uses terms like "less likely", "less probable", "more likely".

I am trying to find the factors that are independently associated with the outcome, hence, I have included all factors of interest in the multivariable analysis. I think parsimony would be more of a concern if I were to build a prediction model (which is not the case here).

[sturu]

I'm not dogmatic about my approach, & others who respond will have a more formal statistical education, but for what it's worth:

I think your understanding of the probability-based terminology of Bayesian stats simply reflects the underlying differences between the two philosophies, though I'm no expert here. Certainly Bayesian models allow pinpoint predictions of probability to be recovered from simulating two outcomes, while this does not follow naturally from the frequentist approach.

I don't believe there's anything to stop you using odds in the Bayesian framework. I've seen this done many times in scientific literature in some fields. It may be technically against the philosophy - not sure. On the other hand I've heard a few Bayesian statisticians warn against trying to interpret the individual model parameters, and instead recommend comparing two predictions from the fitted model using two datasets (e.g. the unaltered dataset & one where one/more variables have been changed by a set amount). This allows you to calculate stuff like Conditional Effects including full parameter distributions for these effects. Luckily this is fairly simple in this framework just by prediction & subtraction. For logistic regression you'd compare the predicted probabilities rather than the predicted binary outcomes.

What follows is actually inaccurate, but hopefully helpful to understand this output. More detail later:

(assuming arm::bayesglm uses MCMC) I expect the coef.est in the model summary will be the mean of the chain of estimates for each of the coefficients on the logit scale. They are summaries of the estimates for the Betas. Similarly the coef.se are likely to be the standard error of the estimates of each of the coefficients on the logit scale. You could convert the pinpoint estimates to odds with exp(Beta), and you could create odds ratios by dividing through by the odds of a reference class.

The same can be done for the coef.se values by calculating the coef.est +/- coef.se and exponentiating to find the upper and lower se bounds, then subtracting the point estimate.

The reason I say it's technically incorrect is that you're taking the mean of a (a priori) gaussian distribution on the logistic scale, then converting it back to the natural scale where there's no guarantee that the mean corresponds to the mean/median of the now transformed distribution of parameter estimates. Your pinpoint estimate of the odds will be biased by the transformation, as will the credible intervals.

As I understand it, the a more accurate way to retrieve odds ratios from a Bayesian model would be to use the full posterior distribution (the MCMC draws), and transform these back to the natural scale by exponentiating. You have a distribution of parameter estimates on the natural scale, which is no longer gaussian, even if the posterior distribution remained gaussian on the logit scale. You would summarise this transformed distribution as you like - OR +/- 95% Credible Intervals, or OR +/- 95% Highest Posterior Density.

Coming from a background in applied science, I was taught to create models using stepwise approaches & retain variables with p values <0.2. Clearly this is impossible in the Bayesian framework, & I'm very greatful that I've learned better ways to create models. If you haven't looked into it, I'd advise reading on model selection using WAIC, or LOO criteria. This link may be useful:

Vehtari Model Selection Tutorial

In writing this response I came across this paper. I haven't read it, but I suspect it will really help you:

Starkweather -Bayesian Statistics in R

& finally I can't recommend Richard McElreath's Lecture series enough - it was like turning on the lights in my brain:

McElreath - Statistical Rethinking

Hope that's helpful & not too much that's misleading.

All the best,

Stuart