Are there alternatives for forecasting time-series data when you have more underlying data available than used in the standard time-series forecasting models?

[lgirola]

I've worked through time-series forecasting models and have mostly relied on Hyndman, R.J., & Athanasopoulos, G. (2021) Forecasting: principles and practice , 3rd edition, OTexts: Melbourne, Australia. Forecasting: Principles and Practice (3rd ed) (last accessed on February 20, 2023).

I'm testing models such as ETS, ARIMA, and vector autoregression. I've created a hypothetical where I assume I have only the first [12] months of time-series data and I forecast for months [13-24] based on the actuals for months [1-12]. I generate simulation paths for months [13-24], and distributions thereof. I then compare those forecasted simulation paths/distributions for months [13-24] with the actual data for months 13-24 in order to assess forecast reasonableness. Results using ETS and ARIMA have been fine, with some minor adjustment such as using logs.

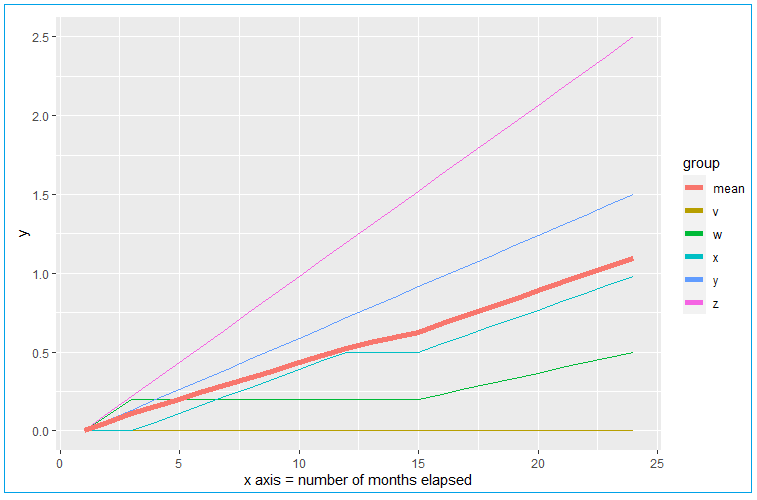
However, these traditional time-series forecasting methods analyze/forecast essentially a single-line, depicted as the heavier trend line in the below image using my example data and labeled mean. In my data, that heavier trend line is simply an average of many underlying elements with disparate trends. The below is a simplified example of my actual data for the sake of post replicability and all of my actual curves take the form of nice smooth logarithmic functions. In the below example, there are elements v, w, x, y, and z, and their mean is mean in the example data frame. But the trends of the underlying elements in my actual data do look like this example data in terms of dispersion around the mean. Values never fall below zero.

For time-series forecasting such as for this form of example data, are there any other methods I should be considering, that take into account the additional information I have at hand for the many underlying elements? (In my actual data I have 48 months and 60,000 + elements trending over those 48 months).

Code to generate the above:

library(ggplot2)

DF <- data.frame(
  mo = 1:24,
  v = c(rep(0,24)),
  w = c(0,0.1,rep(0.2,12),seq(0.2,0.5,length.out=10)),
  x = c(0,0,seq(0,0.5,length.out = 10),0.5,0.5,seq(0.5,0.98,length.out = 10)),
  y = seq(0, 1.5, length.out = 24),
  z = seq(0, 2.5, length.out = 24)
)

DF$mean <- rowMeans(DF[,2:6])

DF_reshape <- data.frame(
  x = DF$mo,                           
  y = c(DF$v, DF$w, DF$x,DF$y,DF$z,DF$mean),
  group = c(rep("v", nrow(DF)),
            rep("w", nrow(DF)),
            rep("x", nrow(DF)),
            rep("y", nrow(DF)),
            rep("z", nrow(DF)),
            rep("mean", nrow(DF))
            )
  )

ggplot(DF_reshape, aes(x, y, col = group)) +  
  geom_line() +
  geom_line(data = filter(DF_reshape,group == "mean"), linewidth = 2) +
  labs(x = "x axis = number of months elapsed") 

---

^{Referred here by Forecasting: Principles and Practice, by Rob J Hyndman and George Athanasopoulos}

[technocrat]

@lgirola

(In my actual data I have 48 months

For a forecast horizon h = 12, the text notes

Most time series models do not work well for very long time series. The problem is that real data do not come from the models we use. When the number of observations is not large (say up to about 200) the models often work well as an approximation to whatever process generated the data. But eventually we will have enough data that the difference between the true process and the model starts to become more obvious. An additional problem is that the optimisation of the parameters becomes more time consuming because of the number of observations involved.

This suggests

1. Adding the additional 36 months of data should be ok
2. Adding 6e4 parameters is probably not (and not only due to processing burden)

It would be surprising if all the 6e4 elements varied independently or have equal salience to the aggregate influence on the forecast. There may be low variability/high impact drivers as well as high variability/low impact, etc. On the other hand, there might be insight to be gained by TSLM for elements that can be expected to have influence. Or, possibly, do bootstrap sampling of the mean.