Hi. I have a dataset with various independent variables, and scores similar to credit scores as my dependent variable. The complication is that the scores are only given in quintiles, such as a score between 0 and 19 is given as a 1, 20 to 39 is given as a 2, etc. Do I treat these scores as numeric or as factors? Thank you.
My suggestion: ordered factor. Use factor and specify levels, or just set ordered as TRUE.
I would rephrase the question: Is credit score as the dependent/response variable better treated as continuous or categorical? Is the goal prediction or classification?
My goal is prediction.
As I understand it, regression will create dummy variables of a variable that is declared as a factor.
What is the effect of ordering the levels? Why does that matter in a regression? Does it matter in other algorithms?
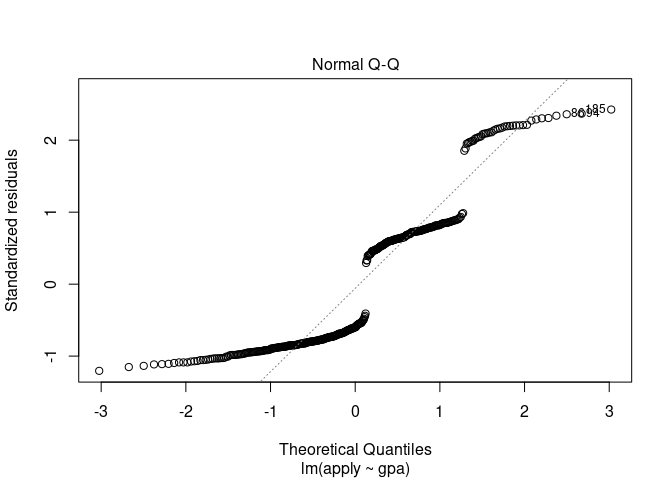
This is analogous to categorizing the scores into bins. The assumption of normality of residuals is violated.
# Load libraries
library(haven)
# Read in data
odata <- read_dta("https://stats.idre.ucla.edu/stat/data/ologit.dta")
# ols model with the single quantitative predictor
misfit <- lm(apply ~ gpa, data = odata)
summary(misfit)
#>
#> Call:
#> lm(formula = apply ~ gpa, data = odata)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -0.7917 -0.5554 -0.3962 0.4786 1.6012
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) -0.22016 0.25224 -0.873 0.38329
#> gpa 0.25681 0.08338 3.080 0.00221 **
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 0.6628 on 398 degrees of freedom
#> Multiple R-squared: 0.02328, Adjusted R-squared: 0.02083
#> F-statistic: 9.486 on 1 and 398 DF, p-value: 0.002214
plot(misfit,2)
# changing response variable to a factor throws an error
odata$apply <- factor(odata$apply)
misfit <- lm(apply ~ gpa, data = odata)
#> Warning in model.response(mf, "numeric"): using type = "numeric" with a factor
#> response will be ignored
#> Warning in Ops.factor(y, z$residuals): '-' not meaningful for factors
Why would normality of the errors matter with 400 obseravtions?
Linear models assume that the response is continuous and the error has a normal distribution.
Linear models do not necessarily assume the error has a normal distribution. For example, the Gauss-Markov theorem does not depend on the error distribution being normal.
Having a normal distribution matters for some things, although very few things if there are a large number of observations.
You’re right on both counts, and I shouldn’t have overgeneralized. For purposes of queuing up a predictive analysis of an ordinal response I wanted to steer thinking away from OLS where the problems seem obvious.
Yeah, getting the equation right is the most important thing. Couldn't agree more.
I was actually suggesting ordinal logistic model, not OLS. But may be there are other and possibly better alternatives as well.
This topic was automatically closed 7 days after the last reply. New replies are no longer allowed.
If you have a query related to it or one of the replies, start a new topic and refer back with a link.